6.2.3 滑模变结构控制
1）滑模变结构控制简介。
变结构控制（variable structure control，VSC）本质上是一类特殊的非线性控制，其非线性表现为控制的不连续性。这种控制策略与其他控制的不同之处在于系统的结构并不固定，而是可以在动态过程中，根据系统当前的状态（如偏差及其各阶导数等）在目的地不断变化，迫使系统按照预定滑动模态的状态轨迹运动，所以又常称变结构控制为滑动模态控制（sliding mode control，SMC），即滑模变结构控制。滑动模态可以进行设计且与对象参数及扰动无关，这就使得变结构控制具有快速响应、对参数变化及扰动不灵敏、无需系统在线辨识、物理实现简单等缺点。该方法的缺点在于当状态轨迹达到滑模面后，难以严格地沿着滑面向着平衡点滑动，而是在滑模面两侧来回穿越，从而产生颤动。
滑模变结构控制是变结构控制系统的一种控制策略。这种控制策略与常规控制的根本区别在于控制的不连续性，即一种使系统“结构”随时间变化的开关特性。该控制特性可以迫使系统在一定特性下沿规定的状态轨迹作小幅度、高频率的上下运动，即所谓的滑动模态或滑模运动。这种滑动模态是可以设计的，且与系统的参数及扰动无关。这样，处于滑模运动的系统就具有很好的鲁棒性。
（1）滑动模态定义及数学表达。考虑一般的情况，在系统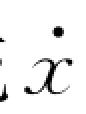
＝f（x），x∈R n 的状态空间中，有一个切换面s（x）＝s（x 1，x 2，…，x n）＝0，它将状态空间分成上下两个部分：s＞0及s＜0。在切换面上的运动点有三种情况，如图6.7所示。
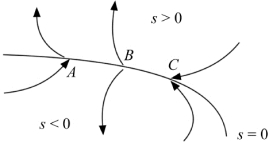
图6.7 切换面上三种点的特性
通常点：系统运动点运动到切换面s＝0附近时，穿越此点而过（点A）；
起始点：系统运动点到达切换面s＝0附近时，从切换面的两边离开该点（点B）；
终止点：系统运动点到达切换面s＝0附近时，从切换面两边趋向于该点（点C）。
在滑模变结构中，通常点与起始点无多大意义，而终止点有特殊的含义。因为如果在切换面上某一区域内所有的运动点都是终止点，那么一旦运动点趋向于该区域，就会被“吸引”到该区域内运动。此时，称在切换面s＝0上所有运动点都是终止点的区域为滑动模态区，或简称为滑模区。系统在滑模区中的运动就叫作滑模运动。
按照滑动模态区上的运动点都必须是终止点这一要求，当运动点到达切换面s（x）＝0附近时，必有：
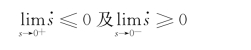
或者：
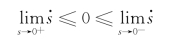
也可以写成：
此不等式对系统提出了一个形如
的李雅普诺夫（Lyapunov）函数的必要条件，由于在切换面邻域内函数式（6-37）是正定的，而按照式（6-36），s 2的导数是负半定的，也就是说在s＝0附近v是一个非增函数，因此，如果满足条件式（6-36），则式（6-37）是系统的一个条件李雅普诺夫函数，系统本身也就稳定于条件s＝0。
（2）滑模变结构控制的基本问题。设有一控制系统：
需要确定切换函数：
求解控制函数：
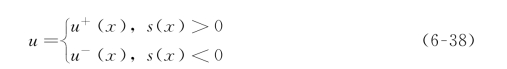
其中，u＋（x）≠u－ （x），使得：
①滑动模态存在，即式（6-38）成立；
②满足可达性条件，在切换面s（x）＝0以外的运动点都将于有限的时间内到达切换面；
③保证滑模运动的稳定性；
④达到控制系统的动态品质要求。
前三点是滑模变结构控制的三个基本问题，只有满足了这三个条件的控制才叫滑模变结构控制。
（3）滑模变结构控制系统设计。滑模变结构控制系统要求系统在任意状态能够在一定时间内到达滑动平面，并且能够在滑动平面稳定运行，这包含两个问题：滑动平面s（x）的选择和控制函数U（x）的设计。滑动平面s（x）能保证系统方程解的存在和系统动态响应性能，控制函数U（x）设计保证系统能够到达滑动平面，滑动平面处处都是运动终止点，在滑动平面形成滑模区。
滑动平面根据不同的输入有不同的形式。对于单输入系统而言，滑动平面为一维函数，对于多输入系统而言，滑动平面为多维函数。例如系统有m 个控制，就有m 个滑动平面，不论输入数量如何，归根结底都是滑动平面系数C 的选择，C 一般为矩阵形式。
控制系统在单输入情况下，滑动平面为：
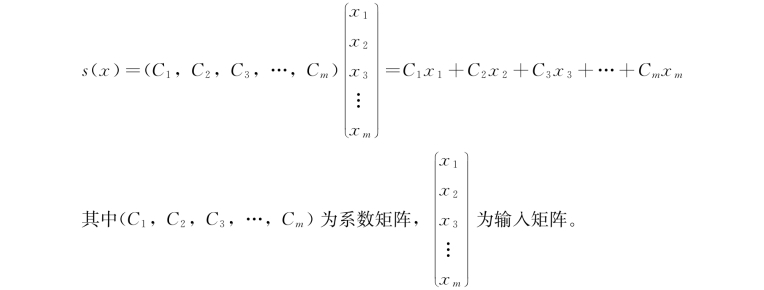
为了保证系统能够到达滑动平面，且使滑动平面处处为终止点，常用的几种控制函数U（x）有以下几种：
①等速趋近律：
②指数趋近律：
③幂次趋近律：
④一般趋近律：
不论哪种形式的控制函数，都要保证系统能够在指定时间内到达滑动平面，并在滑动平面持续运动，既要避免控制系统的滞后控制，又要防止系统的过饱和控制，保证系统稳定运行。
2）基于滑模变结构算法的控制器设计。
∣Δi∣为系统内部模型和外界干扰之和。
（1）位置控制器的设计。将位置子系统看作三个二阶的子系统，分别用于控制飞行器三轴方向上的平移运动，每个二阶的子系统都是严格反馈控制，根据期望信号和对应反馈信号结合滑模控制算法和Lyapunov函数来设计位置控制律。下面以z 通道为例，介绍基于滑模控制的位置控制器的推导过程。
z 通道的状态空间方程为：
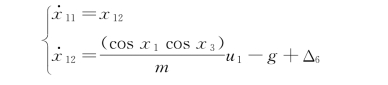
定义z轴位置跟踪误差ez＝x 11d－x 11，其中x 11d 为z轴的期望位置坐标z r，x 11 为飞行器在飞行过程中z 轴的实际位置坐标。
定义滑模切换面为：
则其导数为：
然后将u 1 作为已知量，同理可推导出水平通道的控制律：
系统运行过程中考虑到四旋翼飞行器的安全飞行，对滚转角和俯仰角的范围给出如下约束条件：
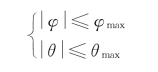
作如下变量代换：
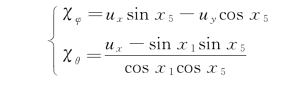
（2）姿态控制器的设计。将姿态子系统看作三个二阶的子系统，分别用于控制飞行器绕三轴的旋转运动。显然，每个二阶的子系统都是严格反馈控制。下面以滚转角通道为例，介绍基于滑模控制的姿态控制器的推导过程。
φ 通道的状态空间方程为：
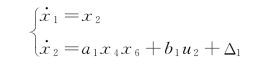
定义滚转角跟踪误差eφ＝x 1d－x 1，其中x 1d为期望滚转角φd，x 1为飞行器在飞行过程中实际滚转角。
定义滑模切换面为：
则其导数为：
同理可得，俯仰角、偏航角的控制律为：
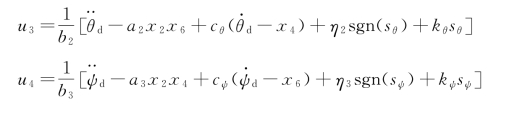
