一、抽象思维
(一)对抽象思维的认识
数学抽象,指对实际生活中含有数量、空间等属性的物质材料进行加工,从中得出的具有共性的本质特征,得以用数学语言进行表述,最终成为一般化的数学理论的过程。其作用如下。
1.数学抽象存在于数学教学过程中
数学概念、数学法则和数学规律等的推导都需要经历抽象概括的过程。数学抽象存在于一切数学问题的计算、推理和建模中。
2.数学抽象具有层次性
数学理论在发展过程中呈现出逐渐抽象的特征。例如从“结绳记数”到所有自然数,再到后继数,然后到无限的正整数序列,从而形成了正整数集合N;从整数到分数,从有理数到实数等都是逐步抽象的过程。
(二)抽象思维的应用
数学作为研究数量和空间的学科,其研究的并非具体的数量关系和空间形式,而是抽象的,数学处处存在抽象思维。具体而言,哪里有数学,哪里就有抽象思维,其不同之处仅在于呈现的方式不同。
数字伴随学生整个数学学习阶段。学生在学习1~10,11~20,21~30……的过程,学生对数学的抽象层次在不断地提高,之后逐渐认识更加抽象的无穷数、分数、小数、负数等。
从计算角度来看,数学计算也具有抽象性,比如最简单的“2 + 3= 5”,对于小学生来说,可能需要借助实物和直观图进行理解,他们并不一定掌握了抽象的原理。
(三)抽象思维的教学
小学数学教师在教学过程中一般会结合小学生的心理特点和认知规律,用一种更为直观的方式将抽象的数学知识呈现在小学生面前,最后在恰当的时机讲解抽象原理,从而提高小学生的数学思维能力,帮助学生理解数学的本质。比如在讲解几何图形时,教师多采用几何直观的形式进行教学,但这并非数学教学的最终目标,其教学根本目的在于通过直观手段帮助学生理解几何图形的概念、性质和原理。抽象的深度大致分为三个阶段。
(1)简约阶段:将复杂的数学问题进行简化,从而得出事物的本质,这是最基础也是最重要的环节。
(2)符号阶段:将具体内容剔除,借助图形和符号来表述某类事物。
(3)普适阶段:建立假设,在推理的基础上构建数学法则和模型,能够从一般的意义解释具体的事物。
当前的数学课堂教学模式主要以创设情境为主,其次将数学知识进行抽象,通过建模来说明和运用数学原理。但这种教学模式常常忽视了简约阶段,使得数学教学不够全面和完整。
在情境数学教学中,小学数学教学阶段往往忽视了抽象思维的教学,这不利于锻炼学生的抽象思维。因此,小学数学教师在运用直观手段教学的同时,应在遵循小学生认知规律的基础上,适当选择合适的教学时机体现抽象数学思维,以有效训练学生的数学能力,提高学生运用数学知识解决实际生活中的问题的能力,这也符合《数学课程标准》的要求。
案例:有一条河,河中心有两个岛,一共有七座桥,如图4-1所示,一个人如何能不重复、不遗漏地一次走完七座桥而返回原处?
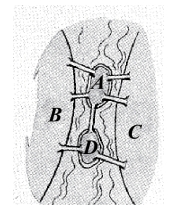
图4-1
这个问题有点像几何问题,但是与传统的几何图形的形状和大小无关。想要解决这个问题,就需要将图中的陆地和岛屿抽象成数学中的一个点,将桥抽象成数学中的线,如图4-2所示。这样就能将这个复杂的路线问题简单地抽象成数学中的几何图形问题。
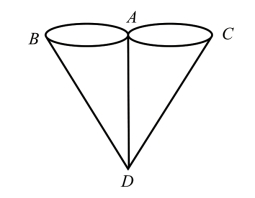
图4-2
对这一图形的形状加以分析:这样的形状一般有一个起点与终点,若二点重叠则视为特殊情况。除了起点和终点外,图中各端点的连线可以视为若干组一进一出的偶数条,这样的点就称为偶点,否则为奇点。想要不重复、不遗漏地一笔完成图形,起点和终点必须是奇点,奇点的个数只能为0或2。
在上述图形中存在A、B、C、D四个奇点,说明人们不管怎么走都不可能一次不重复、不遗漏地走完七座桥并回到原处。所以,该题无解。
