“吃透”学生,减少教学的盲目性——以“角的度量”为例
在教“图形与几何”的教学过程中,教师不可忽视学生对角的度量能力。对于小学生而言,能够借助工具准确度量出角的度数是一项基础的数学技能。在开始学习角的度量知识时,学生已对长度、面积等度量对象有了一定了解,但“角”与长度、面积有着较大差别,如测量工具不一样,前者为直尺,后者为量角器;又如,测量复杂度不一样,前者只需要查看单一方向的刻度即可,而后者测量时需根据情况判断是看内圈刻度还是外圈刻度。但两者的度量性质却是一致的,因而,前者的测量经历势必会对后者的测量产生一定的影响。
针对这一情况,教师在设计教学方案时应当考虑学生现有的知识水平,着力打破他们在思维上的定势,采取有效的教学活动激发学生的学习自主性,使他们能够以富有创造性的方式完成学习任务。换言之,教师应以学生为中心,准确把握其学习情况,将他们“吃透”,精准定位“教”与“学”的着力点,减少或避免盲目性的教学。此处以“角的度量”教学内容为例,探讨如何实现以上目标。
(一)课前检测
我在课前对学生进行检测,从某校四年级中选取两个班作为测试对象,共计102名学生。
1.学习难点调查
【问题1】你认为角有大小吗?
对前测结果进行统计后发现,有87人的答案为肯定,15人的答案为否定,正确率为85.3%。
【问题2】观察下面的角,你知道怎样比较它们的大小吗?

关于比较∠1和∠2的大小,学生普遍认为:一个角为锐角(∠1),一个角为钝角(∠2),而锐角比钝角小,所以∠1<∠2。由于学生已熟练掌握了锐角与钝角的知识,因此正确率为100%。
关于比较∠3和∠4的大小,出现了三种情况:其一,78人认为∠3>∠4,他们的说法是∠3在外面;其二,15人认为∠3<∠4,其理由是将∠4视作三角尺中的直角再与∠3对比;其三,剩余的9人无法判断。
【问题3】你知道如何测量角吗?
(1)为了测量角的大小,你会选择何种工具?(见图6-13),请把你所选择的工具序号填入( )内,并说一说为什么。

图6-13 测量工具
在选择量角工具时,有8人认为④不可以用来量角的大小,因为角均是由两条直线构成的,曲线工具不具备量直线的功能。有56人选择了④,他们说出这种工具名为量角器,专门用于测量角的度数。由此可知,超过半数的学生认识量角器,但不太清楚它的具体用法。
(2)观察(图6-14),你能准确测量出下列角的度数吗?请利用你所选择的工具,测量以下3个角的大小,并说说你是如何测量的。
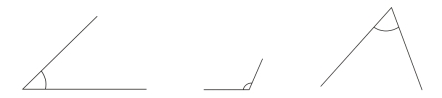
图6-14 测量角的大小
数据显示,仅有17个学生能完成对三个角的测量并得出准确答案,仅占测试总体的16.7%。对于第一个角的测量,学生的完成率和准确率最高,完成率为100%,准确率为36.3%;而第二个角的测量准确率最低,仅占18.6%。由此可知,学生当前并不知道如何正确地度量角。
2.学习难点分析
(1)不熟悉量角器的构造以及它的功能。
(2)市面上的量角器形形色色,有的设计较为复杂,学生不熟悉其使用方法,有的难以准确定位量角器上的角,有的不能将量角器的“角”与需要测量的“角”重合,因而难以测量出角的度数。
(3)分不清什么时候该看内圈,什么时候该看外圈。在图6-14中,第二个角需要看外圈的度数,但仅有19人的结果是准确的。
(二)课堂实施
1.注重基本活动经验的积累
数学这一学科涵盖了各种各样的知识和技能,它们的要点各不相同,因而要培养学生的数学素养势必需要经历一个长期的复杂过程,且在此过程中必须讲究方法的科学性和有效性。这就要求教师在教学中充分扮演好引导者的角色,带领所有学生通过不同的教学活动激发他们的学习热情和探索兴趣,使其掌握数学基础知识,并熟练运用所学知识解决现实问题,积淀基本的数学活动经验,亲身体会数学的魅力。
基于此,可设计如下课堂教学步骤:活动角的操作→角度开口由小变大→180°角、360°角→1°角→使用量角器度量。
2.借助动画辅助教学
量角器上刻画了很多线条和数字,因而在教师介绍其用法时,学生较易将概念混淆,因而学习效果并不理想。教师可借助动画(见图6-15)辅助教学,一方面利用动画将知识点生动地呈现出来,方便学生理解记忆;另一方面,动画中有声音和色彩,更容易吸引学生的注意力,引起学生的学习兴趣。
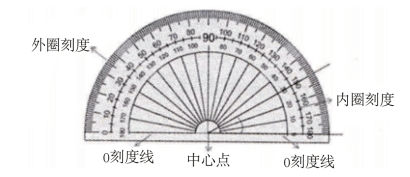
图6-15 量角器动画演示图
3.找准度量角的重难点
根据课前检测结果不难发现,学生在测量角的大小时,难以准确区分什么时候该读取内圈刻度,什么时候该读取外圈刻度。因此,教师在讲解此环节的内容时,应当将以上两种情况分开解说,使学生熟知两者的区别,以此提高他们测量角度的准确性。具体流程如下。
首先出示开口朝右边的角(见图6-16)。
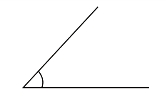
图6-16 开口朝右的角
然后出示开口朝左边的角(见图6-17)。
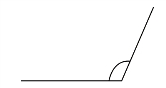
图6-17 开口朝左的角
通过以上两个角的对比,学生能够清楚认识内圈与外圈刻度存在的意义。测量第一个角时,读取内圈刻度即可得到它的度数,而测量第二个角时若继续读取内圈刻度便会发现其度数小于90°,但它为钝角,度数应大于90°,学生此时便会意识到这样读取的答案是错误的,转为读取外圈刻度。
4.选择丰富的素材,提高实效
不同朝向的角在测量和读取刻度时有着不同的难度,因而为了避免学生在测量上存在盲区,教师应尽可能选择不一样的练习素材,帮助学生熟悉各种角的测量方法,以此保证练习的有效性。具体的练习素材见图6-18所示。
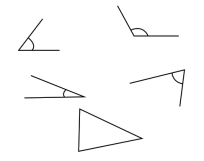
图6-18 练习素材示例
5.熟记量角器的运用方法(“二合一看”)
(1)第一步为合,即使量角器的中心与角的顶点重合。
(2)第二步为合,即使量角器的右侧0刻度线与角的一条边重合。
(3)第三步为看,即看角的另一条边指向的量角器的内(外)圈读数。
(三)课后检测
在课后,我再一次检测学生的学习情况,测试对象与前测对象相同,仍为该两个班102名学生。
1.检测题目
请观察以下角(见图6-19),你能准确测量出它的度数吗?请试一试。
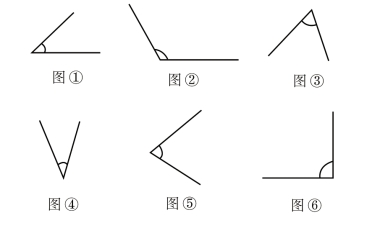
图6-19 测量角的度数
2.检测结果(见下表6-12)
表6-12 四年级(X)、(Y)班课后检测结果

3.测试分析
表6-12中的检测结果表明,学生在学习本课后,已知如何测量角的大小,也学会了区分哪一种角需读取内圈刻度,哪一种角需读取外圈刻度,但他们对于不规则角的测量仍存在问题,如测量图③④⑤中的角的正确率明显低于其他角的测量,尤其是图⑤中的角的测量正确率仅有53%。究其原因,以上三个角的开口朝向不同于一般的角,分别为朝下、朝上、朝右下,相对其他的角,它们的操作难度更大,且图⑤中的角的度数为72.5°,学生会误认为是74°。因此可以看出学生在测量时并不细心,不会灵活运用测量方法。如角的两条射线较短时,可以将其适当延长以便与刻度线更好重合,提高测量的准确性。而对于一般的锐角、钝角以及直角,大部分学生都能够准确测量出它们的度数。
(四)课例思考策略分析
通过对“角的度量”一课的教学研究可以发现,学生的认知水平、思维方式、学习习惯等直接制约着教学过程和结果。因此,广大小学数学教师应首先“吃透”学生,了解他们的实际学习情况以及疑难点,然后据此设计适应性更高的教学方案。也只有能够紧紧吸引学生注意力的教学内容才能够更好地引导学生联想、操作以及反思与交流,从而促进其空间观念的发展。基于此,为了进一步提高学生的学习成效,教师在后续课堂教学中应注意以下几点。
(1)让学生自主探索量角器内、外圈刻度设计的缘由。
(2)在掌握量角要领时,操作过程中的“二合一看”一定要精准。
(3)安排不同开口方向、不同度数的角的测量,如朝左上、左下、右上、右下方开口的角,或者如52°、94°、107°等非整数度数的角。
(4)为提高测量的准确度,教师可提醒学生将角的边适当延长,并留下辅助延长线的痕迹,但需注意的是,所作线条不可过粗,读数也要精准。
