二、类比推理
(一)对类比推理的认识
类比推理,指根据两种事物的相似性,认为两种相似的事物存在一样的性质的推理方法,其特征是“从特殊到特殊”。类比法得出的结论不一定为真,需要进一步论证。比如,将整数的运算律类比到小数中,可得出小数有着与整数一样的运算律的结论。
类比推理与归纳推理既有联系,也有区别。从联系的角度看,用类比推理和归纳推理得出的结论都是待定的;从区别的角度看,类比法是从特殊到特殊的推理过程,归纳推理是从特殊到一般的推理过程。
(二)类比推理的应用
类比推理是一种合情推理方法,可应用于生活的各个领域。比如,人们根据鸟的飞行特性发明了飞机,根据鱼的特性发明了潜艇,等等。
此外,类比推理是探索数学问题的重要工具,其在小学数学中的应用详细见表4-5。
表4-5 类比推理在小学数学教学中的应用
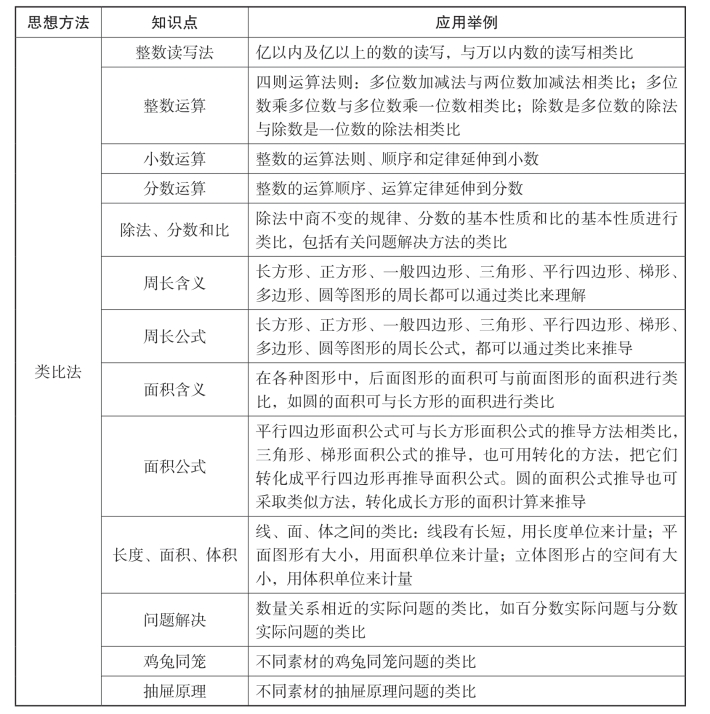
(三)类比推理的教学
用类比推理方法能够有效利用已有知识来解决新的数学问题。将新知识和新问题同已有的知识进行类比,可以更快地找出解决办法,提高学生的类比思维能力。在进行类比的过程中,有的类比显得直接,有的类比显得隐秘,直接的类比分析起来比较简单,隐秘的类比分析起来较为复杂。教师帮助学生树立类比的思想,首先要锻炼学生的观察、比较和联想能力。
在小学数学教学过程中,类比推理教学主要包括以下几类。
1.类比概念
小学阶段所要掌握的数学定义对小学生来说有一定难度,教师可以采用类比的方法帮助学生理解数学概念,比如学习圆的周长和面积概念,就可以类比之前所学的长方形、正方形的周长和面积概念,来加深对圆的周长和面积概念的理解。
2.类型性质
小学数学知识中的性质,如商不变性质,小数、分数的性质等性质之间存在一定的关联性,如根据小数的性质,可将小数转化成分数,以此类比出分数的性质。
3.类比法则
小学数学中小数和整数的计算法则存在密切的联系,如依据十进制计数的特性能够类比出四则运算法则。
4.类比定律
小学生在了解整数的运算律后能够采用类比推理的方法得出小数和分数的运算律。
5.类比代数与算术
小学阶段,学生已经初步学习了用字母表示数和一元一次方程问题,这其实是代数式运算的法则和运算律的内容,小学教材并未明确提出这些知识点,但小学生在解决问题的过程中实际上就用到了类比法。
6.类比立体和平面
小学生在学习立体图形时可以借助已学的平面图形知识进行类比,如由面积的概念和公式类比出体积的概念和公式。
7.类比曲线与直线
在小学阶段学习的平面图形中,三角形、长方形都是由直线围成的,圆和扇形则是由曲线围成的。直线围成的图形和曲线围成的图形存在相似之处。小学数学在推导圆的面积公式的时候,采用“割补转化”的方式,事实上就应用了类比法,我们也可以根据三角形面积公式来类比圆的面积公式,这里就是将圆的弧长视为三角形的底,圆的半径视为三角形的高。
案例:对下列式子进行观察,能够得出什么结论?
(1)9>3,9+1>3+1;95>93,95+6>93+6;112<119,112+7<119+7;156<171,156+10<171+10;
9>3,9-1>3-1;95>93,95-6>93-6;112<119,112-7<119-7;156<171,156-10<171-10。
(2)9>3,9×1>3×1;95>93,95×6>93×6;112<119,112×7<119×7;156<171,156×10<171×10;
9>3,9÷5>3÷5;95>93,95÷6>93÷6;112<119,112÷7<119÷7;156<171,156÷10<171÷10。
分析:上述用“>”或“<”连接的式子,称为“不等式”,小学阶段学习了等式的性质,对不等式进行类比,可得出以下结论。
(1)不等式的两边同时加上或减去相同的数,不等号的方向不变;
(2)不等式的两边同时乘以或除以相同的正数,不等号的方向不变。
