三、演绎推理
(一)对演绎推理的认识
小学阶段的演绎推理主要包括三段论、选言推理、假言推理和关系推理几种类型,具体如下。
1.直言三段论
直言三段论是演绎推理的一般模式,包括大前提、小前提和结论三个部分,即由两个前提得出一个结论的形式。比如所有的三角形内角和为180°,锐角三角形是三角形,所以锐角三角形的内角和为180°。所有的三角形内角和必然不是360°,锐角三角形是三角形,所以锐角三角形的内角和必然不是360°。
在三段论中,大前提和小前提包含的共同项为“中项”,上述中的“三角形”为中项,大前提和结论包含的共同项为“大项”,上述中的“内角和为180°”为大项,小前提和结论包含的共同项为“小项”,上述中“锐角三角形”是小项。用字母S表示小项,M表示中项,P表示大项,其一般推理形式为:
所有的M都是P;
S是M;
所以,S是P。
三段论的核心思想在于:当某类事物的全部具有或者不具有某种性质时,该事物的部分也全部具有或者不具有某类属性。上述举的两个例子可以用图4-9来表示。
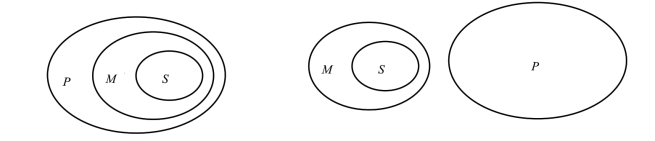
图4-9 三段论演示
2.选言推理
选言推理包括相容选言推理和不相容选言推理。这里重点介绍不相容选言推理。大前提为不相容的选言判断,小前提为对其中一个选言支进行肯定,结论为否定其他选言支。比如一个四边形要么是平行四边形,要么是梯形,要么是不规则四边形。如果这个四边形不是平行四边形和不规则四边形,则它是梯形。
3.假言推理
这里着重说明充分条件的假言推论。对前提有个充分条件的假言判断,确定先件就是确定后件,否定后件就是否定先件。比如,如果一个数的末尾是0,那么这个数能被5整除;如505,末尾是0,所以505能被5整除。这里的大前提是一个假言判断,与直言三段论存在区别。
4.关系推理
关系推理,指前提中至少有一个是关系命题的推理,主要有以下几种形式:
(1)对称性关系推理。比如1dm=10cm,所以10cm=1dm。
(2)反对称性关系推理。比如m小于n,所以n不小于m。
(3)传递性关系推理。比如10>5,5>2,所以10>2。
(二)演绎推理的应用
小学数学很多问题都应用了演绎推理方法,不过小学的演绎推理并没有严密的证明推理过程。比如已知平行四边形的面积公式后,在推导三角形面积公式时,是将两个完全一样的三角形组成一个平行四边形,再由平行四边形的面积公式“底乘高”推理出三角形的面积公式为:底乘高除以2。
演绎推理在小学数学阶段中的应用见表4-6。
表4-6 演绎推理在小学数学阶段中的应用
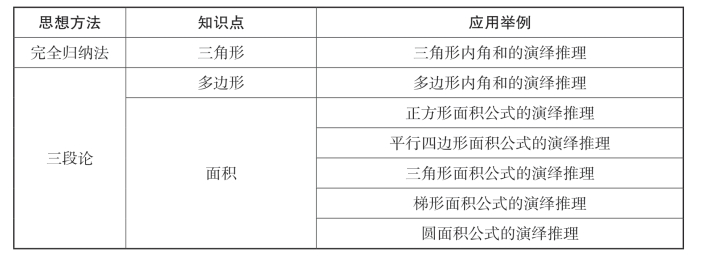
续表
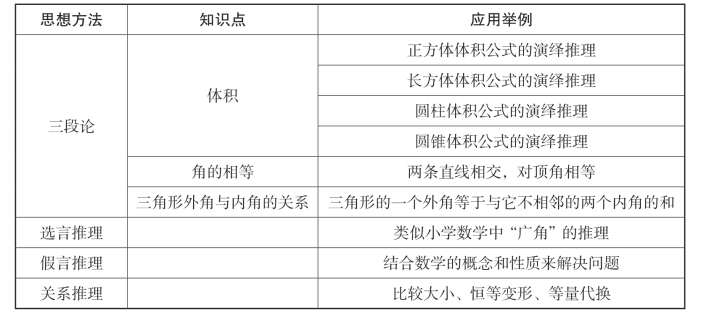
除此之外,演绎推理方法在小学数学问题中还有许多应用,如用正反比例图像分析数据,借助数轴的直观性对比分数的大小等。
(三)演绎推理的教学
《小学数学课程标准》要求学生在小学数学阶段就具备一定的推理能力,指出演绎推理教学应当渗透到教学的各个环节,潜移默化地影响学生的推理思维。在义务教育教学过程中,教师应当摒弃“形式主义”思维,在教学时注重学生推理的逻辑性、条理性,在观察学生思考和探究的活动中,引导学生运用正确的思路解决问题,让学生认识到推理过程和方法的重要性。
不同年龄阶段的小学生有着不同的认知水平、学习特点和心理特征。据研究表明,学生的推理能力在四年级(10岁左右)时有较大的飞跃,能够根据命题找出联系,得出结论。由此可见,这一阶段是学生思维能力形成的关键期,需要教师重点关注。有关演绎推理能力发展的四个阶段如下。
(1)简单的原理和法则的直接运算(如小学四则演算)。
(2)简单原理和法则以字母为形式的运算(如加法交换律的一般公式:a+b=b+a)。
(3)将算数原理、法则视为大前提,能够有条理地进行推理,得出新的结论,完成课堂练习。
(4)以初等代数和几何原理为大前提,进行合乎逻辑的推理,从而找出新的结论和规律。
演绎推理包括演绎和推理两个部分,小学生只有将二者有机地统一起来,才能初步形成一定的演绎推理能力,推理的过程具有条理性。在小学数学教学过程中,发展小学生的演绎推理能力需要考虑以下几个方面。
1.推理是数学的基本思维方式之一
推理对学习数学有着事半功倍的作用,渗透到数学教学的全过程。在小学数学教学过程中,推理和运算是解题常用的思路。找规律、归纳法则,面积和体积公式的推理,无不用到推理思维。因此,小学数学教师要将培养学生的推理思维视为系统的工程,将推理思维贯穿教学的始终。
2.兼顾合情推理和演绎推理
合情推理,指根据事物固有的特性去归纳出一般的结论的方法;演绎推理是根据一般的结论有条理地推导新的结论。二者对解决数学问题都起到十分重要的作用,教师需要平衡好二者的关系,在教学时不能顾此失彼。
3.将推理思维与数学各个领域的知识结合起来
在小学数学教学过程中,教师要注重在数学各个领域、各个环节中渗透逻辑推理思维,在一些饶有挑战性的探究和猜想案例中锻炼学生的推理能力,提高学生的数学综合应用能力。
4.把握推理教学的层次性和差异性
在推理思想教学过程中,教师应当在遵循小学生认知规律的基础上,充分考虑小学生接受的可能性和教材内容,制订科学的教学方案来提高学生的推理思维能力。
在小学数学阶段,演绎推理能力在数学中的教学目标见表4-7。
表4-7 演绎推理能力在小学数学中的教学目标

尽管小学生的认知水平有限,用演绎推理开展数学教学工作存在一定的困难。但相关研究发现,学生如果在小学时具备了一定的演绎推理能力,对下一阶段的初中数学演绎推理的学习具有较大的帮助。因此,小学数学教师需要在平时的教学中为学生逐渐渗透演绎推理的思维。
案例:规定两种新的预算法则,“●”表示两个数取其大,“○”表示两个数取其小。比如4●6=6,9○12=9,现计算5●7+15○18的大小。
分析,根据“●”表示两个数取其大,所以5●7=7,根据“○”表示两个数取其小,所以15○18=15。因此,5●7+15○18=7+15=22。
