一、模型思想
(一)对模型思想的认识
在数学学习过程中,模型思想是常用的一种解题思路。模型思想,指借用数学符号和语言,对现实生活中事物的性质、数量关系和空间形式通过建立模型的方式进行分析和理解。从广泛性层面来看,数学知识的概念、性质和定理等都是一种数学模型,数学模型以数学符号、图标等形式为主,与符号化思想存在一定的联系。对数学模型的理解有助于加深对数学知识在经济、物理、生物等方面的应用,推动社会的发展。
这里重点讨论小学阶段数学模型的建构。数学模型作为一种数学工具,将加工后的生活信息加以推理,分析和预测相应的情况,从而指导我们的实践活动。数学模型在信息时代中的应用十分广泛。如在计算机领域应用数学模型,能够完成大量的数据计算和处理;在生物医疗领域应用数学模型,能够帮助人们完成许多精细的体力劳动。
构建数学模型旨在解决生活中的实际问题。因此,在小学数学教学中,教师要注重小学生数学模型思维的构建,帮助学生掌握一定的知识和技能,指导学生的实践活动,增强学生运用数学模型思维解决各种生活问题的能力。
(二)模型思想的应用
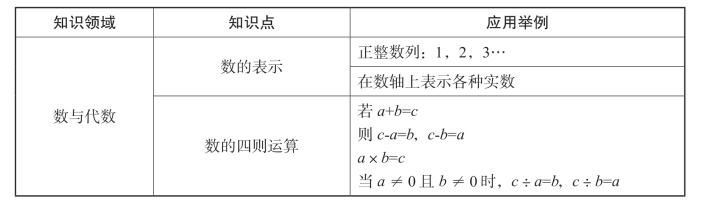
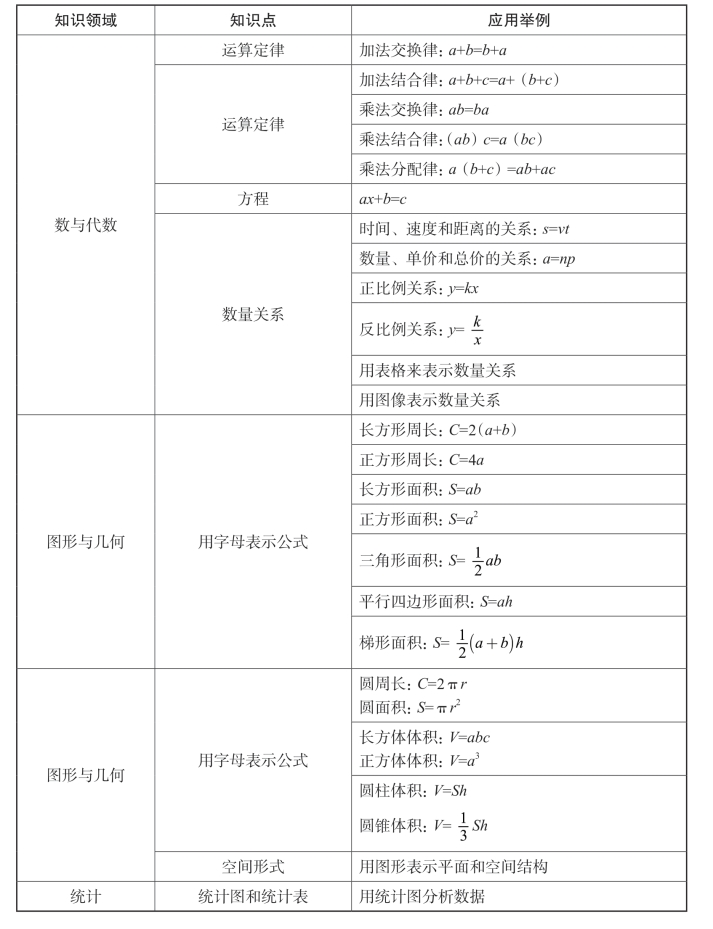
构建数学模型的过程实际上就是应用数学知识的过程。数学模型是伴随着数学知识的出现而产生的,同时,大量的数学知识也是借助数学模型得以解决的。在小学数学阶段,数学模型的具体应用如表4-11所示。
表4-11 数学模型在小学数学教学中的具体应用
续表
(三)模型思想的教学
事实上,模型思想借助符号和图形的形式是对数量关系和空间形式的抽象,这一点与符号化思想是一致的。但模型思想强调通过建立抽象的模型,为解决生产生活中的问题提供指导。因此,在小学数学教学过程中,小学教师要将模型思想贯穿于教学的各个环节,同时引导学生在构建数学模型中激发学生学习数学的热情,锻炼学生的思维能力。
树立数学模型思想,一方面要求学生掌握基本的数学模型思维;另一方面,要求学生能够用构建的数学模型去解决生活中遇到的各类问题。建模的具体步骤如下。
(1)理解问题的背景,明确需要用何种模型来解决何种问题。
(2)将复杂的情境简化,收集各种数据。
(3)用数学关系式或者图形的形式构建模型。
(4)用数字模型解决实际问题。
总的来说,学生在构建数学模型过程中,需要依赖现有的数学知识结构对生活中的数量关系和空间形式深入分析,在深入思考的基础上进行建模,从而指导生活实践,解决相关问题。因此,小学数学教师在建模过程中,不仅要帮助学生学会构建数学模型,理解数学模型的意义,从表面的数学符号分析数学知识的本质,同时还要引导学生借助数学模型解决生活中的实际问题。
