变中有不变思想
（一）对变中有不变思想的认识
数学教学的目的在于帮助学生从变化中找出相对不变的数学性质和规律，这就要求学生逐步树立“变中有不变”的思想。比如，经过系统的数学知识学习后，学生就能明白除法、分数和比之间尽管表面不同，但本质上都是数值之间的比例关系。
小学数学作为学生打好数学基础的阶段，对学生今后的数学学习起着关键作用。小学数学知识内容不多，难度不大，但由于小学生自身的认知特点，学生在学习数学过程中存在一定困难。因此，小学数学教材编排主要采用分散式、直观的、从具体到抽象的编排方式。然而这种编排方式可能导致学生理解的数学知识过于浅显和片面。因此，在小学数学教材的编排和教学中，体现变中有不变的思想是有必要的。
（二）变中有不变思想的应用
变中有不变的思想在数学的概念、法则、规律等各个方面都有所体现。比如对整数的认识，其本质都是利用十进位值制计数的原理来认识和学习数。我们深入地理解可知，小数事实上也是整数十进位值的拓展。
对于数学运算规律的归纳也是从整数入手，再延伸到小数、分数、有理数的。由此可见，运算律在实数的范畴内都是适用的。
学生在数学学习中树立变中有不变思想，能够透过数学知识的表象抓住其内在特征和本质规律。比如总价等于单价与数量的乘积，这一规律能够适用一切情境的商品买卖，也能够帮助学生建立起相应的数学模型进行分析。
（三）变中有不变思想的教学
学生数学知识和技能的获取、数学思维方式的掌握，都离不开变中有不变的思想，离不开对数学本质的分析，这也是新课改的内在要求。教师引导学生透过数学表象把握数学内在规律，对于理解数学知识，提高数学能力都有一定的帮助，有利于提高学生运用数学知识解决实际问题的能力。
案例：如图4-7，每个小正方形方格边长为1cm，以线段AB为一条边，要求分别画出一个面积为3cm2的三角形、一个面积为6cm2的平行四边形和一个面积为7cm2的梯形。
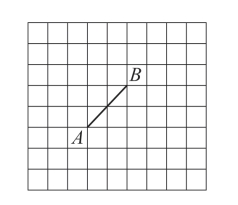
图4-7
分析：第一问，要求三角形的面积为3cm2，根据三角形面积公式，
，可以计算出ah=6，理论上能够画出无数个。第二问，根据平行四边形面积公式S=ah，可得出ah=6。第三问，根据梯形面积公式：
，可得出（a+b）h=14，可以假定h=2，a+b=7。部分答案如图4-8所示。
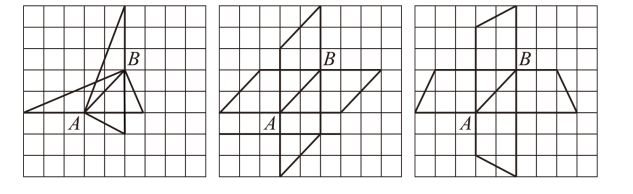
图4-8