四、集合思想
（一）对集合思想的认识
集合，指把具有同类性质的事物看作一个整体，视为一个集合，单个事物成为集合的元素（简称“元”）。其中，这里谈到的“同类性质”是判断一个事物是否属于该集合的标准，但是该集合的前提是必须明确的、具体的。比如，“身高比较高的学生”就不能组成集合，这是因为身高较高的标准是含糊不清的。而“身高在160cm及以上的学生”就能组成一个集合，小刚的身高为165cm就属于该集合，小李的身高为158cm就不属于该集合。
同时，一个给定的集合中的元素不能重复出现。比如集合M={1，2，3，4｝不能写为集合M={1，2，3，4，4}。事实上，集合M只有四个元素。当两个集合的元素完全相同，则这两个集合相等。比如集合P={x｜x=k，1≤k≤4，k∈N}，此时M=P。
集合的描述方式主要有列举法和描述法。列举法，即把集合的所有元素都一一列出，用大括号“{}”括起来表示集合的方法。描述法，指在大括号“{}”内写出某集合元素的某些特性，来说明组合的方式。上述的M、P分别使用了列举法和描述法。当集中的元素有无穷个时，就不应用列举法了，而应用描述法。除了列举法和描述法，韦恩图（封闭的曲线）可以表示集合内部的关系，曲线的内部为集合的各个元素，这种方法更为直观、清晰，如图4-4所示。
图4-4 韦恩图表示集合之间的关系
“一一对应”，即对于一个集合M中的任何一个元素a，在集合N中必然都有元素b与之相应，对于集合N中的任何一个元素b，在集合M中也就必然存在元素a与之相应。例如，正整数集和正奇、偶数集中间的元素可以建立起一一对应的关系。将世界各国建立成一个集合，各国的首都也看作一个集合，这两个集合就可以形成一一对应的关系。
有限集合，指集合中的元素个数是有限的。无限集合，指集合中的元素个数是无限的。可数集合，指集合中的每个元素与自然数集N的每个元素之间能建立一一对应的集合。其中，集合的元素与顺序无关，如集合D={a，b，c}={a，c，b}={b，a，c}。
假设集合M、N，当M中的所有元素都包括在集合N中，那么集合M就是集合N的子集，表示为“M⊆N或者N⊇M”，叫作集合M包含于集合N或者集合N包含集合M。从集合论的角度分析数学知识，有利于把握数学知识的整体和部分之间的关系。比如数的扩展能用集合论的思想进行分析。有关概念用集合来表示更为简洁，更有利于学生把握代数与几何之间的关系。
空集，指不含任何元素的集合，用符号“∅”表示。空集是任何集合的子集，表示为“∅⊆M”。比如一个班级的学生身高在145～165cm之间，那么166cm组成的学生集合就是空集。空集和集合N={0}是两个概念，此时集合N也存在一个元素0，应注意区分二者之间的关系。
（二）集合思想的应用
小学数学中很多知识点都渗透了集合的思想。比如对自然数的概念理解能够从对等集合基数（元素个数）方面入手；集合思想还能应用到数的运算中。在小学数学教学阶段，常用韦恩图来表示图形的关系，比如将所有的三角形视为一个集合，记为“M”，锐角三角形、直角三角形和钝角三角形各自记为“集合A”“集合B”“集合C”，此时集合A、B、C就是集合M的子集，集合M是集合A、B、C的并集。
（三）集合思想的教学
1.正确理解相关的概念
集合是无法直接比较大小的，只有当两个集合中的元素完全相同时，可以认为这两个集合相等。此外，集合之间存在包含与被包含的关系，当集合M中的所有元素都能在集合N中找到，但集合N中存在集合M没有的元素，那么集合M是集合N的真子集，记为“M
N”。通过比较有限集合元素的个数，能够比较基数的大小，如果这两个集合的元素个数相等，说明基数相等，即等势或等基。当集合M是集合N的真子集时，就可以得出M的基数小于N的基数的结论。
比较两个无限集合的大小关系时，只要两个集合的元素能建立一一对应的关系，就说明这两个集合的基数相等。如正整数集合与正偶数集合能够建立图4-5的一一对应关系。因此，可以认为二者的基数相等。
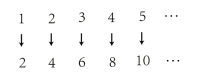
图4-5 正整数集合与正偶数集合的一一对应关系
2.正确把握集合思想的教学要求
集合知识在小学数学阶段并非必须掌握的内容，教师在教学过程中需要坚持适度的原则，对集合思想的描述尽可能直观、生动。比如，在讲解分类计数问题时，教师可以采用直观的韦恩图法进行讲解，提高教学效率。
3.集合思想应当贯穿于小学数学教学的全阶段
集合知识的学习是一个漫长的积累过程。教师帮助学生树立集合思想，需要坚持循序渐进的原则。从小学一年级对数的认识和分类到小学高年级的公因数、公倍数、多边形的分类等都渗透了集合的思想。由此可知，集合思想需要贯穿于小学教学的各个阶段。
案例：班上共45个人，在一次文艺活动中，表演唱歌的有15人，跳舞的有11人，唱歌和跳舞的有9人，班上有多少人没参加节目？
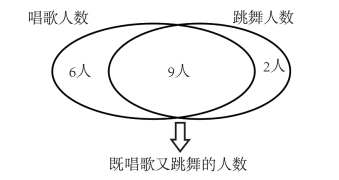
图4-6
对于这道数学问题，可以采用韦恩图的集合思想来分析，如图4-6所示。左圈表示唱歌的人数，右圈表示跳舞的人数，两个圈的重叠部分表示既唱歌又跳舞的人数，有9人，由此可见，唱歌中不跳舞的人数有15-9=6（人），用左圈与右圈不交叉的部分表示；跳舞不唱歌的人数有11-9=2（人），用右圈与左圈不交叉的部分表示。最终得出参加节目的人数有6+2+9=17（人），则没参加节目的人数有45-17=28（人）。