三、分类思想
(一)对分类思想的认识
分类思想,指当面对一个整体的数学问题难以下手时,通常将其按照一定的分类标准划分为若干部分,分别进行讨论,即“分而治之,逐个击破”。分类的具体步骤如下。
(1)确定同一种类型的分类标准。
(2)在标准下对研究对象进行分类,要求不重复也不遗漏。
(3)逐个进行讨论。
(4)进行总结,得出结论。
分类讨论思想不仅应用于数学学科领域,还应用于社会学科、人文学科等多个学科。《数学课程标准》中对学生的要求是:在数学思维的指导下,对数学问题能够有序地、全面地且符合逻辑地进行思考。由此可见,分类讨论思想有利于解决数学中的难题,提高学生数学的综合应用能力,培养学生良好的数学思维。但教师在引导学生使用分类思想的过程中,需要考虑适用性问题,要做到对数学问题的全面理解。
学生在学习数学知识时,从学习的宏观层面深入到微观层面,有利于透过现象分析事物的本质,形成和发展数学能力,构建属于自己的数学知识体系。同时,学生在使用分类讨论的思想时,也应用到了集合的思想、概率和统计的思想,这些思想之间存在密切的联系。
(二)分类思想的应用
在小学数学教学过程中,分类思想无处不在。从宏观的角度看,根据分类思想,小学数学可以分为数与代数、图形与几何、统计与概率、综合与实践四大板块。从微观层面进行划分,小学生在学习负数后,对数的认知范围进入有理数,有理数分为整数和分数,整数分为正整数、零和负整数,整数根据它的整除性分为偶数和奇数。正整数分为1、素数和合数。
由此可见,分类思想有助于帮助学生理解数学知识之间的联系性,提高其数学的实际应用能力。比如,在分析数学的排列组合问题时,学生就可以使用分类讨论的方式加以解决。关于小学阶段分类思想在数学中的应用,如表4-2所示。
表4-2 分类思想在小学数学中的应用
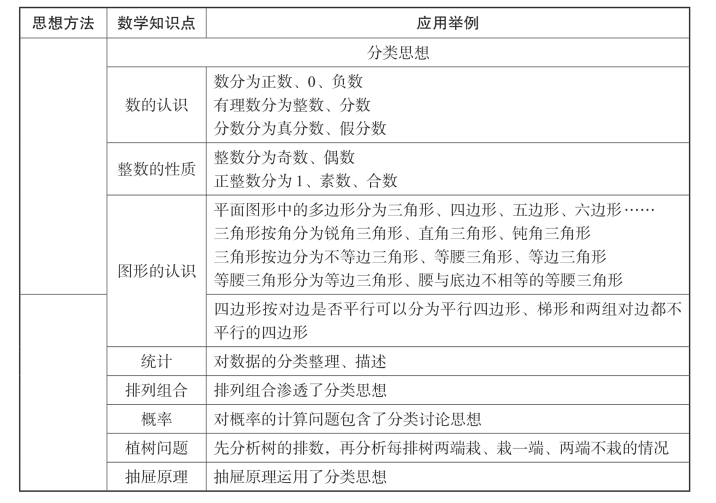
除此之外,分类思想还能应用于数学的正反比例教学中,比如先让学生了解量的相关关系,在此基础上对相关的量进行分类:量的比值一定,量的乘积一定,量的和一定,量的差值一定。从而让学生自主归纳出各组变量之间的关系,加深对正反比例关系的理解。
(三)分类思想的教学
(1)小学数学教师在讲解分类与整理的教学过程中,要注意培养学生的分类思维,如对需要统计的事物进行分类。
(2)在理解数学思维和运用数学知识解决数学问题时,如在进行排列组合、抽屉原理等问题的教学中,需要渗透分类思想。
(3)在讲解统计知识时,注意渗透分类讨论思想。解决统计问题时,教师可以引用生活中的实际案例锻炼学生的分类思维能力。
(4)在数的认识、图形的认识等教学时,教师应当注重集合思维和分类思维的渗透。
(5)运用分类思想进行数学教学时,教师要让学生明白分类的目的,通过数学知识有效解决现实生活中的问题,使数学回归生活,指导生活。
(6)在渗透分类思想过程中,教师要注重数学问题在一般条件下的适用性和特殊情况下的不适用性。如果教师在讲解数学知识的过程中忽视了其特殊的不适用性,则可能导致学生数学思维的不全面。比如对于判断题“如果6a=9b,则a:b=9:6”,这道判断题漏掉了a和b为0的情况,因此这道题是错误的,但是在小学数学教学时,有个不成文的规定:讨论整数的性质时,不考虑0的情形。这就使得这道判断题十分有争议,设置问题的严谨性不足,不利于小学生下一阶段的数学学习。
案例:数一数,图4-3中有多少个长方形?

图4-3
分析:根据分类思想,我们可将图4-3中的图形分为以下几类。
单一的长方形:2×4=8(个);
两个单一的长方形组成的长方形:10(个)
三个单一的长方形组成的长方形:4(个)
四个单一的长方形组成的长方形:5(个)
六个单一的长方形组成的长方形:2(个)
八个单一的长方形组成的长方形:1(个)
长方形总个数:8+10+4+5+2+1=30(个)
这种分类思想在计算图形的个数方面过程较为复杂,但更便于学生理解。
