一、归纳推理
(一)对归纳推理的认识
归纳推理,指依据某一事物的部分的性质来判断该事物都存在这类性质,从而得出一般性结论的方法,推理特征为“从特殊到一般”。在现实生活中,人们主要利用归纳分析法得到较一般结果。归纳分析法主要包括完全归纳法、不完全归纳分析法。完全归纳法,即根据某一事件中的任何一种事件都具有一定特性,进而确定该事件具有这类特性的归结方法。例如,根据铁、铜等的导电性确定了一切金属材料都具有导电性的结论。由于完全归纳法是通过对全部子事件加以推论,因此得到的结果也必然为真。不完全归纳法是指通过子事件中的部分对象来推论该事件具有一定特征的归结方法,其得出的结论不一定为真,需要进一步论证。数学归纳法能够根据数的性质对事物进行推断,相当于一种完全归纳法。
这里讨论的归纳法,如未做说明,一般指不完全归纳法。
事实上,数学史上许多问题,如哥德巴赫猜想(任一大于2的偶数都可写成两个素数之和),都是靠归纳法提出来的著名数学问题,至今未有人能证实这一猜想,我国著名的数学家陈景润也只是证明了“任一充分大的偶数都可以表示成二个素数的和,或是一个素数和另一个素数的和”。
(二)归纳推理的应用
归纳法是合情推理的方法之一,可以应用到人们生活的方方面面。人们在生活中许多实用的经验都是靠归纳法总结得到的。
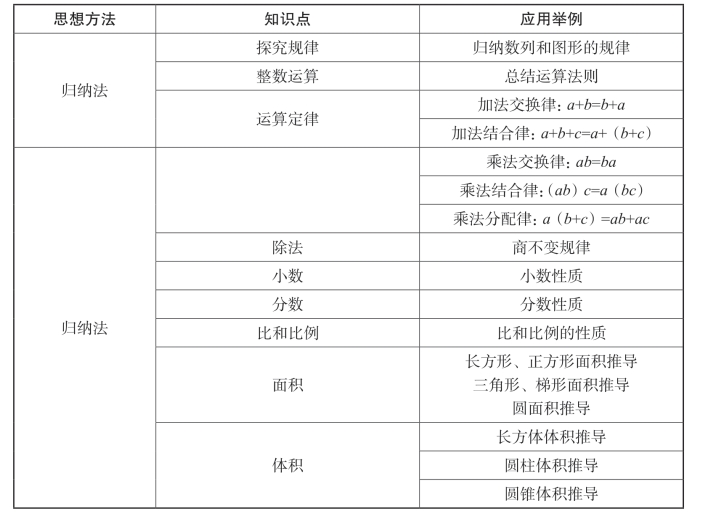
归纳法也渗透到小学数学教学中。小学数学的很多公式、规律都是借助一些典型例子再归纳得到的。归纳法在小学数学的应用详见表4-3所示。
表4-3 归纳法在小学数学中的应用
(三)归纳推理的教学
小学数学阶段的归纳推理教学重点是培养学生在图形和数的排列方面的归纳推理能力,小学生的推理发展水平主要分为以下阶段。
阶段一:算术运算的直接归纳推理,如由“0+1=1,0+2=2,0+9=9,0+21=21……”得出“任何数加零都是原来的数”。
阶段二:简单文字运算的直接归纳推理,如由“m=n,m+a=n+a,m+b=n+b,m+c=n+c……”得出“等式两边加相同的数,等式仍然成立”。
阶段三:算术运算的间接归纳推理,如由分数运算得出分数的性质。
阶段四:初步代数式的间接归纳推理,如由多次分析两个变量的关系归纳出 y= f(x)的函数式。
在小学数学教学实践中,小学生的归纳推理能力与年龄成正比,一般来说,随着年龄的增长,小学生的归纳推理能力会逐渐提高。不同学生的归纳推理能力也存在一定的差异。因此,在小学数学归纳推理教学过程中,教师要在遵循学生认识规律的同时,注重学生的个体差异性。
小学数学教学阶段的归纳推理能力教学目标见表4-4。
表4-4 小学数学阶段归纳推理能力教学目标

小学数学阶段的归纳推理主要有法则的归纳、性质的归纳、公式的归纳、定律的归纳和规律的归纳,详述如下。
1.法则的归纳
在整数的四则运算教学中,首先是让学生明白基本的算术方法,其次对运算方法进行总结和归纳。比如多位数乘以一位数,就需要学生先掌握乘法口诀、口算和笔算方法,再利用竖式计算方式来归纳出其运算法则。
2.性质的归纳
商不变的性质,小数、分数的性质,比和比例的性质等都是在对几个典型例子分析的基础上,最后归纳得出来的。
3.公式的归纳
小学阶段的数学公式主要有图形的周长、面积和体积公式,正反比例、比例尺等数学知识的计算。这些计算公式基本上都是在数学教学中探索得出的。
4.定律的归纳
有关整数的加法和乘法运算定律也是在计算几组算式的基础上归纳出来的。比如在推理乘法的交换律时,先计算12×13=13×12,17×19=19×17,34×57=57×34,最后得出一般定律:ab=ba。
5.规律的归纳
小学数学知识涉及的规律有图形、数列和算式的规律,乘除的变化规律等,这些规律也是对一些实例进行对比和分析,再提出猜想归纳得到的。对于小学生来说,想要对规律进行证明有一定的难度,这时候就需要用到归纳法,对某些个例进行验证来归纳出一般性规律。
案例:观察下列算式,能发现什么规律?
1=12
1+3=4=22
1+3+5=9=32
1+3+5+7=?
……
1+3+5+7+…+99=?
分析:该题是从1开始的奇数的加法算式,后一组数比前一组数多一个后继的奇数,第一组数是1个奇数,为12;第二组数是2个奇数相加,为22;第三组数,是3个奇数相加,为32;由此可猜想,第四组数是4个奇数相加,应该是42;“1+3+5+7+…+99”是50个奇数相加,应该是502。由此归纳出一般性的结论,从1开始,前m个连续奇数相加等于m的平方。
即:1+3+5+7+…+(2m-1)=m2。
