找准起点,有的放矢地提升素养——以“三位数乘两位数”为例
随着社会的进一步发展,大众对数学这一门学科提出了更高的要求,与数学学习相关的数学素养也因此备受关注,如何培养、发展学生的数学素养也成为近年来数学教育领域的重要环节之一。数学素养包含多个方面,如数学建模、数学运算、数学分析等。此处主要阐述“数学运算”的培养。通俗来说,数学运算即培养学生的运算能力,它指的是能够根据运算法则和运算律正确地进行运算的能力。此种能力的培养能够加深学生对运算算理的理解,使其学会运用合适且简便的方法解题,从而快速地得出准确答案。为发展学生的运算能力,此处以人教版四年级(上)数学教材中某单元中“三位数乘两位数”为例展开探讨。“三位数乘两位数”笔算是在“两位数乘一位数”笔算乘法和“两位数乘两位数”笔算乘法的基础上进行教学的。两位数乘两位数和三位数乘两位数的算理相同,只要学生熟练掌握了前者,再恰当地利用迁移,一般均能够轻松掌握三位数乘两位数的笔算。为了能精准定位学生的知识水平,我在课前组织了一次前测。
(一)课前检测(简称为前测)
1.前测内容
前测单
(1)C市希望小学共有21间教室,每一间教室中均有38套桌椅,请问该校共有多少套桌椅?
算式:______________________________
竖式:
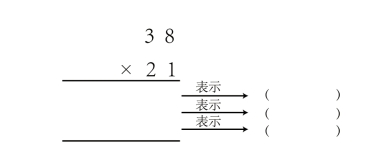
(2)你知道如何进行竖式计算吗?试一试。
124×31=
2.前测的结果(见表6-3)
表6-3 四年(X)班前测结果(共50人)
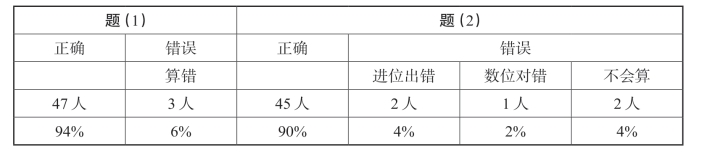
根据表6-3中的结果可以看出,大部分学生均较好地掌握了“三位数乘两位数”的算理以及算法,若能够引导他们对知识进行迁移,教学任务的达成应当较为轻松,因此,我开展开了后续教学设计。
(二)教学实例1
1.教学过程
(1)复习导入,引入新课
①课件出示:中秋节假期,杨阿姨和刘阿姨去省外探亲。她们乘车所花费的时间相同,均为13小时,但两人乘坐的交通工具并不相同。详细信息见表6-4所示。
表6-4 出行信息表

②根据提供的信息,提出数学问题。
预设:1)杨阿姨乘车行驶了多少千米?
2)刘阿姨乘车行驶了多少千米?
3)杨阿姨和刘阿姨乘车一共行驶了多少千米?
4)杨阿姨乘车比刘阿姨乘车少行驶了多少千米?
③学生独立完成计算95×13后,重点交流两位数乘两位数的笔算方法及支撑这种算法背后的道理。
先算95×3得285,再算95×10,得950,将两者相加得1235。95×3求的是3小时行驶的路程,95×10算的是10小时行驶的路程,两者相加即杨阿姨13小时所行驶的路程。
(2)探究新知
试着解决问题2),刘阿姨乘私家车行驶了多少千米?
①估算109×13。
预设:把109看成110,13看成10,大约是1100。(一个估大,一个估小,结果比较接近准确数)
②尝试用竖式计算。
1)学生尝试
学生在学习单上试着计算。注意:竖式计算,可能会出现哪些错误?
2)学生汇报
先算3乘109,怎么写?积的末尾跟个位对齐。再算10乘109,怎么写?积的末尾要跟十位对齐。最后,把它们的积相加。
教师引导学生理解运算背后的道理:要算13小时的路程,可以先算3个小时所经过的路程,再算10个小时所经过的路程,然后将两部分相加,结果即为所求答案。
3)展示对可能会出现的错误的猜想
典型错例有三种:其一,乘十位的1时,积的末尾放错了;其二,没有进位;其三,没乘完。
4)小结
计算三位数乘两位数,用三位数分别与两位数的个位和十位相乘,最后将乘积再相加。要注意与十位相乘时,积的末尾要与十位对齐,需要进位时不要忘了进位。
③比较计算三位数乘两位数和两位数乘两位数的异同点。
(3)巩固练习
你知道如何计算吗?请试一试。
148×53 258×74
2.后测
此次教学实践课开展得十分顺利,在完成巩固练习习题时,我发现学生对三位数乘两位数的算理和法则理解得较为透彻,与前测结果大体相同,所以,这节课即使没有老师教,让学生自主学习也能够收获较好的成果。于是,我在课后又组织了一次后测,结果却令人惊讶,答案的准确率大幅度下降,从94%降为70%,有15名学生的答案是错误的。
(1)后测单
四年(×)班后测单
竖式计算:
365×42=
(2)后测结果见表6-5。
表6-5 四年(X)班后测结果(共50人)
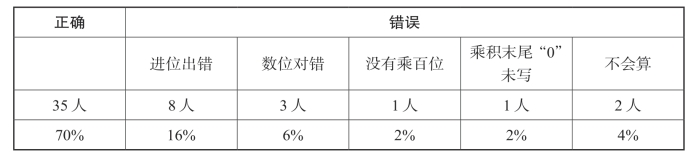
3.教后反思
根据后测的结果可以看出,学生的学习成效并不理想。基于此,我必须对教学设计进行调整和改进。在教学实践中(包括前测、课堂教学)不难发现,多数学生基本掌握了三位数乘两位数的算理和算法,但由于其运算能力较差,因而无法计算出正确结果。从表6-5可以清楚地看到导致学生计算失误的主要原因是进位出错,当乘积出现进位时,学生会在下一次的乘积中忘记加进位上来的几,或因为口算能力弱导致进位加错,当出现连续进位时,学生的错误率就更高。据此可知,学生所欠缺的并非是知识,而是运算能力。因而,在后续的教学设计中可以有针对性地加强运算能力的训练力度。
(三)教学实例2
1.教学过程
(1)复习导入,引入新课
①课件出示:中秋节假期,杨阿姨和刘阿姨去省外探亲。她们乘车所花费的时间相同,均为13小时,但两人乘坐的交通工具并不相同。详细信息见表6-6所示。
表6-6 出行信息表

②根据提供的信息,提出数学问题。
预设:1)杨阿姨乘车行驶了多少千米?
2)刘阿姨乘车行驶了多少千米?
3)杨阿姨和刘阿姨乘车一共行驶了多少千米?
4)杨阿姨乘车比刘阿姨乘车少行驶了多少千米?
③学生独立完成计算95×13后,重点交流两位数乘两位数的笔算方法及支撑这种算法背后的道理。
先算95×3,得285,再算95×10,得950,将两者相加得1235。95×3求的是3小时行驶的路程,95×10算的是10小时行驶的路程,两者相加即杨阿姨13小时所行驶的路程。
(2)探究新知
试着解决问题2),刘阿姨乘私家车行驶了多少千米?
①估算109×13。
预设:把109看成110,13看成10,大约是1100。(一个估大,一个估小,结果比较接近准确数)
②尝试用竖式计算。
1)学生在学习单上试着计算。
学习单 姓名:________
算式:108×13
竖式计算: 猜一猜可能出现错误的地方在哪里?(请列举,至少三点)
2)学生汇报
先算3乘109,怎么写?积的末尾跟个位对齐。再算10乘109,怎么写?积的末尾要跟十位对齐。最后,把它们的积相加。
教师引导学生理解这样运算背后的道理:即要算13小时的路程,可以先算3个小时的路程,再算10个小时所行驶的路程,然后将两部分相加,结果即为所求。
3)展示对可能会出现的错误的猜想
典型错法有三种:其一,乘十位的1时,积的末尾放错位置了;其二,没有进位;其三,没乘完。(预留出一定时间,让学生充分消化、理解错误的症结所在)
4)小结
计算三位数乘两位数,用三位数分别与两位数的个位和十位相乘,最后再相加。需特别注意的是,与十位相乘时,积的末尾应与十位对齐,并记得进位。
③比较计算三位数乘两位数和两位数乘两位数的异同点,从而迁移出三位数乘三位数的算法。
本节课是在两位数乘两位数的基础上进行教学的,很好地实现了从两位数乘两位数到两位数乘三位数的知识迁移。在学生掌握了三位数乘两位数后,再迁移到三位数乘三位数,巧妙地使学生的新旧知识迁移顺利发生,从而使“自主探究”的学习成为可能。
(3)巩固练习
1)列竖式计算。
323×24 569×45
2)根据下面的乘法算式,可以直接解决以下问题吗?
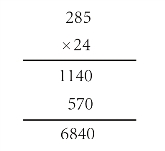
285×4=( );5700÷20=( );
285×4+285×( )=( )。
3)找出下列计算中存在的错误,并修改。
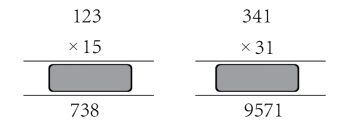
4)以下竖式是下面哪一道题的竖式?

A.532×14 B.224×32 C.358×31
(4)后测
1)后测单。
四年(×)班后测单
竖式计算:
334×55
2)后测结果见表6-7。
表6-7 四年(X)班后测结果(共50人)
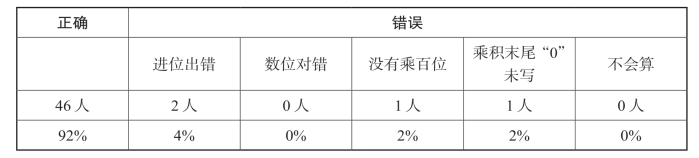
经过教学实例2的课堂教学,我再一次组织了后测,结果表明,学生在连续进位上的正确率有了显著提升,全班只有两名学生在这一方面出错。由此可知,在教学中留足时间,让学生进行三位数乘两位数的笔算练习,并引导他们对计算过程中易错点进行猜测、分析与解决是极有成效的,能够帮助他们准确定位计算要点,减少笔算错误。此外,我在巩固练习中设计了一些变式训练,让学生对笔算过程中的易错点有了更为深入的了解,从而提高其在计算时的警惕性,大大降低了他们出错的概率。不难发现,一节数学课若要取得理想的成果,瞄准教学的起点是十分必要的。
(四)课例思考策略分析
1.找准学习起点,着重解决学生的学习困难
国外一位著名的教学心理学家说:“影响学生学习的最重要原因是学生已经知道了什么,我们应根据学生原有的知识状况进行教学。”国内数学教育界也主张以学生的认知发展水平和已有的知识经验为基础展开教学。这些无不说明着数学学习起点的重要性。因而,数学教师在教学中应该了解并重视学生的学习起点,鼓励他们充分利用现有知识以富有创造性的方式完成学习任务,以此逐步巩固他们的数学基础,从而提升教学的成效。为此,教师应在课前组织前测,以此了解学生对相关知识的掌握程度以及不足之处。然后针对他们在前测中表现出的问题进行针对性的讲解与练习。如针对学生进位的错误,在教学实例2的巩固练习部分加入了一些变式训练,学生学会猜测、分析计算中易出现的错误,以此强化其对进位错误的认知。后测结果表明,学生的进位错误率有了明显降低,这也证明找准学生的学习起点、着重解决其在学习中的为难点是一种可取的教学策略。
2.在比较联系中通算理,强算法
数学这一学科涉及多种不同的算理和算法,虽然它们看似不同,其实内部却有着一定的关联。学生若能在比较中理解、运用,那么学起来、用起来将更为轻松。因此,在教学实例1、2中,均加入了“两位数乘两位数”迁移至“三位数乘两位数”的环节,让学生对比分析两者的算理和算法,在探寻其异同点的过程中明晰两者的联系与区别,逐步加强他们对多位数乘法的理解与记忆。
3.通过变式练习,培养数感,提升运算能力
就学生的数学运算能力而言,若要实现突破,一靠技巧,二靠数感。因而,教师在教学中不仅要设计一些基础性的习题训练,还要设计一些具有针对性的练习。为此,教学实例2的巩固练习部分改变了单纯让学生计算的传统方式,采用留空、留白、充分利用白板课件的优势设计了部分开放性问题,通过观察、比较让学生感悟其中的道理,形式上有新意,内容上不单调,更重要的是,这些练习对培养学生的数感、提升学生的运算能力有着重要的作用。譬如,为了测验学生是否真正掌握了“三位数乘两位数”的算理,我设计了一个根据乘法竖式解决相关问题的题目。学生在寻找正确答案的过程中,不仅要仔细观察竖式中各要素与问题中已知、未知部分的关系,更要综合利用加减乘除等基本运算方法进行试算,以此定位其准确答案。通过这一题型,能够检测出学生对多位数乘法的掌握程度,也能加深其对多位数乘法算理、算法的理解,提升他们的数感和综合运算能力。
