六、几何变换思想
(一)对几何变换思想的认识
数学中的变换包括数与式的恒等变化、图形变换。在初等数学学习中,几何中图形变换的核心思想在于用运动的眼光看待静止的几何事物,这对学生解决数学问题有很大的帮助。
初等几何变换多涉及平面形状在同一平面上的变化,另外还有在中小学阶段的相似变化和合同变换。合同变换,指相似比为1的相似变换,是相似变换的一种特殊类型,具体包括以下几种形式。
1.平移变换
平移变换,指一个图形在变换后得到一个新的图形,二者对应点的连线相互平行且相等,且线段的方向相同。比如平面上的一点M变换得到点N,射线MN就是平移的方向,线段MN的长度就是平移的距离,其性质如下。
(1)经平移变换得到的图形与原图形全等。
(2)平移变换后两点之间的方向不变。比如两点A、M,经变换后得到相应的点B、N,则AM∥BN,AB∥MN,且AM与BN,AB与MN的方向一致。
(3)平移变换后两点之间的距离不变。比如两点A、M,经变换后得到相应的点B、N,则有AM=BN,AB=MN。
具体来说,一个图形在经过平移变换后,得到了一个全新的完全相同的图形,这两个图形上的对应点的连线平行且相等,线段的方向一致,任意两对对应点都能组成一个平行四边形,如图4-12所示。
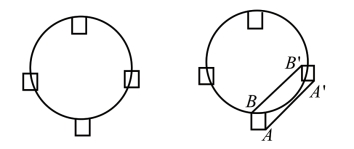
图4-12
在分析初等几何问题的过程中,平移变换是常用的一种方法,它可以将分散的条件集合成一个简单的图形,显得直观、生动。
2.旋转变换
在一个平面中,原点O变换到自身,原点之外的点M变换到M′,使得OM=OM′,∠MOM′=θ(定角),这样的变换就是旋转变换。原点O为旋转中心,角θ为旋转角,当θ>0°时,表示向逆时针方向旋转;当θ<0°时,表示向顺时针方向旋转;当θ为平角时,旋转变换是中心对称。旋转,指一个图形以一个定点为中心,转动一个角度。旋转变换的性质如下。
(1)旋转后的新图形与原来的图形全等。
(2)M、N经旋转变换后得到点A、B,直线MN与直线AB所成的角为θ。
(3)M、N经旋转变换后得到点A、B,则MN=AB。
3.反射变换
在同一个平面内,假设存在一条直线l,平面上的任一点A及其对应点M,直线AM的中垂线与直线l重合,此时的l为对称轴,也叫反射轴,这种平面下的变换叫作反射变换,其性质如下。
(1)反射变换后得到的新图形与原图形全等。
(2)M、N经反射变换后得到点A、B,存在直线MN与直线AB所成的角的平分线l。
(3)M、N经反射变换后得到点A、B,得到MN=AB。
假如一个图形沿着一条直线折叠,直线两旁的部分能够完全重合,这个图形叫作轴对称图形,如图4-13所示。
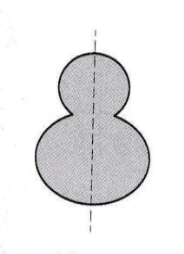
图4-13
如果一个图形沿一条直线折叠,能够与另外一个图形重叠,就可以说这两个图形关于这条直线对称,如图4-14所示。
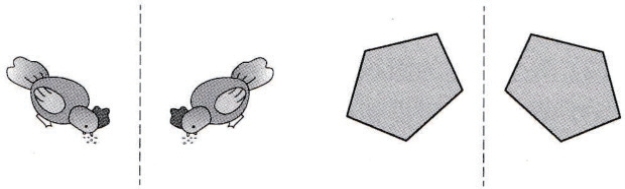
图4-14
轴对称变换,指图像之间的关系和折叠运动;轴对称图形,指的是一个图形,二者存在本质的区别。利用图形的轴对称性可以解决小学数学中的几何计算和证明等问题。
综上所述,经平移变换、旋转变换和轴对称后得到的新图形与原来的图形在形状和大小方面完全相等,都属于保距变换。轴对称图形在一定条件下能够转化为平移变换和旋转变换。比如,将一个图像进行两次轴对称变换,当对称轴平行时,可以看作平移,此时平移的方向与对称轴垂直,平移的距离是两条对称轴距离的两倍;当将一个图形进行两次轴对称变换,对称轴相交,就视为旋转,两条对称轴的交点就是旋转中心,两轴的夹角等于旋转角的两倍。具体见图4-15。
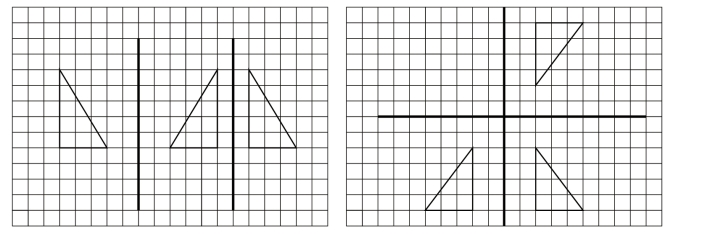
图4-15
4.相似变换
在一个平面中,点M、N经变换后得到点A、B,线段MN变为线段AB,总有AB=k· MN(k>0,且是常数),这类变换就叫作相似变换。具体来说,当某个图形按照一定的比例进行放大或者缩小,其形状不变。其中的k叫作“相似比”或者“相似系数”,当k=1时,就称为合同变换,其性质如下。
(1)变换前的图形与变换后的图形周长比等于相似比。
(2)变换前的图形与变换后的图形面积比等于相似比的平方。
(3)两条直线的夹角不变。
生活中的物体在光线下的投影、照片的放大和缩小等都运用了相似比的原理。“数学上的图形变换来源于生活中物体的平移、旋转和轴对称”,在小学数学教学过程中,小学数学教师应帮助学生分析和了解图形的变换,以锻炼学生的空间想象力,同时使学生发现生活中的设计之美,找到解决实际生活问题的思路。
(二)几何变换思想的应用
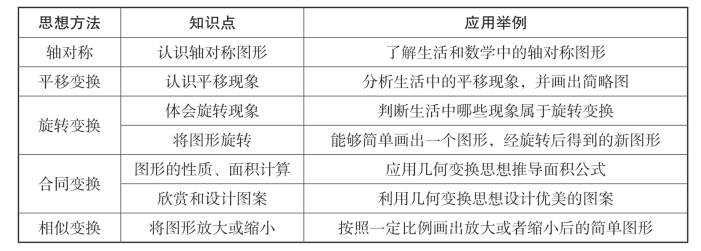
图形变换思想是几何数学中的主要部分,它有助于学习者了解形状的基本特性,推导面积公式,完成几何数学的推导证明等,而几何变换思想在小学数学中的具体运用如表4-9所示。
表4-9 几何变换思想在小学数学教学中的应用
(三)几何变换思想的教学
1.图形变换的教学要求(见表4-10)
表4-10 几何变换思想在小学数学教学中的教学目标

2.教学中应当注意的问题
(1)准确把握变换的概念。数学中的图形变换是对生活中图案的概括和抽象,小学阶段学习的图形变化都是在同一个平面内发生的,且大多不考虑变换的过程,只关注经变换后得到的最终结果。因此,小学生要仔细理解平移、旋转和轴对称图形变换的概念,透过变换的表象抓住数学的本质,从而达到锻炼自身几何变换的思维的目的。
(2)注意图形变换与其他几何知识的联系。小学生在学习平面图形的过程中,一方面要学习有关图形变换的性质和概念;另一方面还要加强对图形本身性质和概念的理解,正确把握变换与图形自身之间的关系,体会图形变换与几何知识的相互转换。
(3)对教学要求和解题思路的正确把握。小学数学教师在讲解图形变换知识时,需要采用适当的教学方法,引导学生正确解答相关数学问题。比如采用直观判断的方式或作图的方式加深小学生对图形变换的理解。
