四、转化思想
(一)对转化思想的认识
在数学学习过程中,学生在遇到用现有知识无法解决的数学问题时,常常会将问题进行转化,从而使数学难题变成一个能够用现有知识予以解决的简单问题,实际上这就用到了转化思想。
数学知识的学习是一个由浅入深,从简单到复杂的过程。在解决复杂的数学问题时,学生借助转化的思想,能够将不熟悉的知识内容转化成熟悉、简单的知识,这种解题思路具有重要的现实意义。
(二)转化思想应当遵循的原则
转化思想的核心在于将难化易,使繁化简,从而解决各种非常规的数学问题,使用转化思维常需要坚持以下原则。
1.数学化原则
数学化原则,即把日常生活中的问题加以数学化,利用数理符号建立思维模式,用数学知识解决实际问题。“数学源于生活,又高于生活。”学习数学的最终目的就是服务于社会生产生活实践,以提高学生用数学知识处理日常生活中各种问题的能力。数学化原则是在处理日常生活中与数学相关的问题时的基础指导思想之一。
2.熟悉化原则
熟悉化原则,指将陌生、不常规的问题转化为熟悉的、常规的问题。随着数学学习的深入,学生今后将会遇到各种全新的知识。学生将这种全新的知识转化成熟悉的内容,有利于提高其探究和创新意识。
3.简单化原则
简单化原则,即将复杂的问题简单化。所谓“万变不离其宗”,复杂的问题实质上是涵盖的知识点多,且过程更为复杂。因此,学生在解决这类问题时,需要找到一些技巧,将其简单化,以助于解题。
4.直观化原则
直观化原则,指将抽象的问题具体化。数学知识是抽象的,直接分析起来比较困难,这就需要小学数学教师在教学过程中,采取直观的方式,将其具体化,这样其解决的难度就大大降低了。
(三)转化思想的应用
学生在解决数学问题的过程中,遇到的问题或是能够直接使用现有知识就能处理的,或是需要综合所学知识进行解答的。小学生学习的数学概念、法则还停留在比较浅显的阶段。因此,他们遇到的数学问题大多是无法直接用现有知识予以解决的,这就需要运用转化思想来解决问题。转化思想在小学数学中的应用如表4-8所示。
表4-8 转化思想在小学数学中的应用
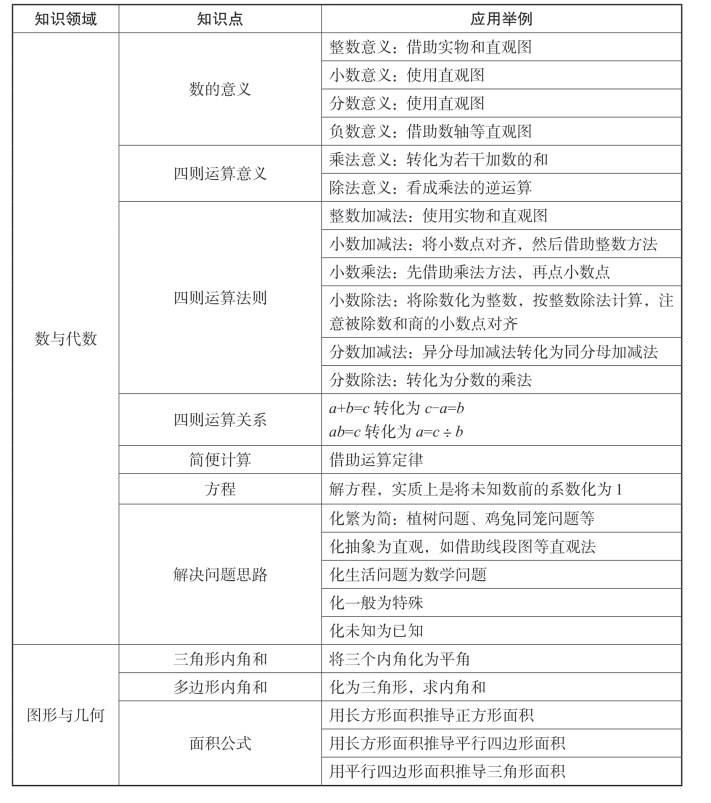
续表
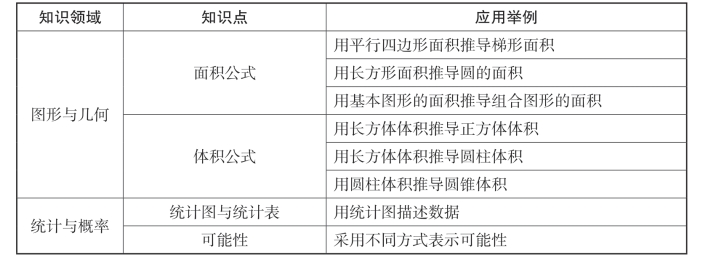
(四)转化思想的教学
小学阶段的转化思想数学教学采用的解题思路有化抽象为具体、化繁为简、化实际为特殊、化未知为已知、化一般为特殊等。在小学数学教学过程中,教师应综合采用各种思路转化教学,锻炼学生的转化思维能力,帮助学生培养用转化思想解决问题的意识和习惯。
案例:小红现有2顶帽子,3件上衣,2条裤子,请问小红一共有多少种搭配方法?
分析:使用分类法和穷举法来解决上述问题,过程十分烦琐,如果采用树状图进行分析,可以直观地解决这一问题。2顶帽子用A、B表示,3件上衣用C、D、E表示,2条裤子用H、I表示,如图4-10所示。

图4-10
由图4-10可知,一共有12种搭配穿法。
