渗透模型思想,培养建模意识——以“单价、数量、总价”为例
某五年级试卷曾出现了这样一道题:“猎豹是陆地上跑得最快的动物,它0.36小时能跑39.6千米,照这样计算,猎豹平均每小时能跑多少千米?”大多数教师原以为学生掌握了小数乘除法的相关知识,可以顺利地将这道题解出来,但结果却与之相反,得出正确答案的学生并不多。部分教师对该题进行分析后发现,学生的失分点在于猎豹奔跑的时间为小数,若将这一小数改为整数,他们应该能够准确列出算式,而此题中猎豹奔跑的时间不足1小时,而是0.36小时,学生在理解“39.6除以0.36的商就是1小时跑的路程”时存在一定困难。这是因为学生在解答试题的过程中一般很难将问题中的要素与“速度、时间、路程”这一数学模型关联起来,所以在解题时会觉得很困难。从这一点不难发现,若要培养学生的解题能力,让学生将所学知识灵活运用于实际生活中,就应当引导他们形成模型思想。
过去,人们并未重视数学模型思想,直到2011年之后,这一个概念才作为核心词被提出来。自此以后,数学模型的构建成了义务教育阶段数学课堂教学的重要环节之一,其价值也日渐凸显。数学模型思想是指通过对问题情境进行抽象,建立数学模型,并用这一模型解决类似问题的策略、意识与观念。就实质而言,即培养学生举一反三的能力,帮助他们形成对知识进行迁移的意识。可以说,模型思想的建立是学生体会和理解数学与外部世界联系的基本途径。在此主要利用课例“单价、数量、总价”来阐述模型思想在教学中的渗透与应用。
(一)教学实例1
“单价、数量、总价”是人教版四年级(上)数学教材中某一单元中的内容,它的目的是让学生在解决实际问题的过程中体会“单价、数量、总价”之间的数量关系,学会将具体问题引申到抽象的数学模型,并运用它来解题。具体而言,这一阶段的教学目标为教师将单价、数量和总价的概念传递给学生,让他们熟悉这三个名词的含义,并了解三者间的数量关系,即“单价×数量=总价”,且能够运用它解答各种各样相关的现实问题,并能够从现实问题中反推出这一数量关系,亲身体会从具体→抽象→具体的归纳路径,形成基本的模型思想。基于此,我在课前组织了一次前测,以增进学生对本课的了解。
1.前测
(1)前测单
①王老师在书城购入了4套一模一样的试卷,共支付了160元,每一套试卷花了多少元?
②上题中的单价、数量、总价分别指的是什么吗?它们之间存在何种关系?
(2)前测结果
很多学生都能够准确给出上题①中的答案。对于第②题,大部分学生能够将这三个量找出来,但并不能清晰地描述它们各自的意义,尤其是单价,鲜有学生的描述是准确而清楚的。而其数量关系,多数学生都知晓。
针对前测中获得的学情情况和对教材的解读,我设计了以下教学环节。
2.教学过程
(1)情境导入、探究新知
教师出示购物小票(见图6-1、图6-2),提炼“单价”“数量”“总价”的概念。

图6-1 购物小票(1)

图6-2 购物小票(2)
师:在日常消费中,总会接触到各种各样的购物小票,如图6-1、图6-2所示,从以上购物小票中你获取了哪些数学信息?请说一说。
师:你看出以上两张购物小票有什么共同点吗?请说一说。
生:都有单价、数量、总价。
师:你能结合小票说一说,什么是单价吗?
师:你还能举例说一说生活中你遇到过的单价吗?
生:一包方便面的价格是2.5元,一双运动鞋的价格为120元,一斤巧克力为32元,一支钢笔为18元,等等。
师:你能总结出什么是单价吗?
生:每件商品的价钱,叫作单价;买了多少,叫作数量;一共用的钱数,叫作总价。
(2)“单价、数量、总价”之间的关系
师:在许多数学问题中也出现了单价、数量、总价。请你说一说下面题中什么是单价,什么是数量。
①运动衫每件95元,买4件需要多少钱?
②梨一斤6元,买5斤要多少钱?
师:我们应该怎么列式?为什么用乘法计算?这两题有什么共同点?
生:已知单价、数量,求总价。
师:从这两题的解答中,你知道单价、数量与总价之间有什么关系吗?
生:单价×数量=总价。
总结:这样的一个算式,叫作数量关系式,我们利用这个数量关系可以解决很多实际问题。
(3)扩展学习,深化关系
不用解答,请你说出下面各题已知什么,求什么,数量关系是什么。
教师出示以下题目。
①每本练习册11元,买90本需要多少钱?
②某超市有优惠活动,樱桃一斤15元,165元能买几斤樱桃?
③教师办公室新买了4台打印机,共花费2560元,每一台打印机多少钱?
总结:这三个数量关系式,就是我们今天所学的单价、数量、总价之间的关系,我们可以根据第一条乘法公式变化得出后面的两条除法公式。这三个关于价格的数量关系式在生活中有着广泛的应用。(数学模型)
(4)随堂练习,巩固新知
①欧老师在体育用品店买了5个一模一样的足球,花了280元,她还需要再买9个一样的足球,请问还需要花多少钱?
②开放题(家庭作业):把题目补充完整并解答。
1)一本练习册9元,______,共需花多少钱?
2)5套试卷共花了60元,______?
3.课后反思
通过引入生活中学生经常能够接触到的购物小票,让他们发现其中有关数学的信息,从而引出单价、数量与总价的含义,然后再借助两个典型例题引出这三者的数量关系式。但对于学生而言,仅仅依靠购物小票和几个简单的例题来阐述单价、数量与总价的概念以及数量关系过于抽象,他们虽然从中得出了有用的信息,但却不能准确说出它们的具体含义,对其关系的了解也并不深入。
课后,我立即对学生们进行检查,发现他们在分析已知条件和求解的过程中习惯性地用乘除法的意义来分析,鲜少借助它们之间的数量关系来理解题意以及求解,由此可知,他们尚未形成成熟的“单价、数量、总价”的模型思想,更谈不上运用它来解答相关问题。
基于此,我对教学设计进行如下调整(见教学实例2)。
(二)教学实例2
1.教学过程
(1)猜一猜,引入单价
①比一比哪位老师买的练习册更便宜,从而引出单价。
王老师和欧老师到书城买练习册,王老师共花了35元,欧老师共花了42元,请试着猜一猜,哪位老师买的练习册更便宜?
师:在这一题目中,要比较哪位教师买的练习册更便宜,比他们花钱的总数多少可以吗?
生:不可以。
师:那比什么?
生1:应该比每一本练习册花了多少钱。
生2:比单价。
师追问:那你说说看,什么是单价?
师:每本练习册的价钱,即它的单价。在数学中,一般将单件商品的价钱称作它的单价。
②生活中的商品单价
出示手套的单价:每一双手套的价钱为15元,15元就是手套的单价。
师:请举例说一说日常生活中你所看到的单价。
出示其他商品,如面包、牛奶、饼干等的单价,指定学生回答。
(2)复合单位,深入理解单价。
①师:出示菠萝10元/个和凤梨10元/斤。
师:菠萝和凤梨的单价相同吗?
生:不相同,虽然它们的标价都是10元,但花10元买到的水果数量并不相同,菠萝可以买到一整个,而凤梨只能买到1斤,因此这两者的单价不一样。
②师:这说明在看货物的单价时,不仅要看它所出示的价钱,还应当关注与这一价钱相对应的量。其实,在日常购物的过程中,我们只要注意观察,就会发现几乎所有商品的单价信息均包含了它的价钱与该价钱相对应的数量的多少。
(3)单价、数量、总价
①引出数量、总价,初步,感知三者的关系。
师出示:运动衫每件95元。
师:请尝试着用简单的方式表示运动衫的单价。
生:95元/件。
师:它是运动衫的单价,那买4件是什么意思?
生:4件是买的运动衫的数量。
师:在数学中,某一类货物买了多少,称作数量。上题的问题是什么?
生:买4件运动衫共需花多少钱。
师:在数学中,“买多个某类商品所花费的钱数,即为总价”。
师:接下来,我们来探讨单价、数量与总价这三者有何关系。上题其实是已知商品的单价和数量,要求它的总价。
②出示表格,发现关系。(见下表6-1)
师:×饮料的单价是多少?这道题求的是什么?如何列式?
师:若还需要买更多罐×饮料,你知道如何算吗?
表6-1 商品信息表
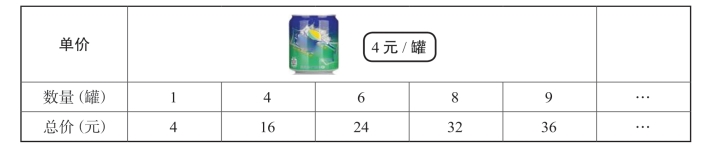
4×1=4(元)
4×4=16(元)
4×6=24(元)
4×8=32(元)
4×8=36(元)
……
师:请同学们仔细观察这一组算式,并说一说你从中看出了什么?
生:在这组算式中,第一个因素为商品的单价,第二个因素为买的数量,而所计算出的为商品的总价。其算式为:单价×数量=总价。它正是单价、数量、总价三者之间的数量关系。
③由单价、数量、总价之间的变化关系,渗透函数思想。
师:除此之外,你们还能在表格中找出其他规律吗?
生:当商品的单价一样,买的数量增加,所需花费的总价也会随之增加。
生:单价相同,数量越多,总价越高。
(4)练习巩固
①牛奶的单价是65元/件,买3件需要多少钱?
问:这道题已知什么,求什么?我们应该运用哪一种数量关系式来计算?
②每本练习本为1.5元,______,共需花多少钱?
问:这道题缺少了什么条件?请将它补齐并试着解题。
③出示缺损的购物清单(见表6-2)。
表6-2 购物清单

问:请说出表6-2中不清楚的部分是什么内容?应如何计算?为什么?
④通过解决变式的问题,师生共同总结“单价、数量、总价”之间另外的两个关系。
师:在解题过程中,可以依据第一条乘法关系式变化得出后面的两条除法关系式。这三个关于“单价、数量、总价”的数量关系式在现实生活中运用得极为广泛。
2.课后反思
在学生经历了教学实例2的教学过程后,我再一次组织了学习检测。通过这次检测,我发现学生在对于单价的描述方面有了显著进步,且对单价、数量和总价这三者的关系有了进一步认识。究其缘由可知,调整后的教学设计中有几个环节针对性更强,能加深学生对三者关系的认知,具体如下。
(1)猜一猜引入单价环节能够有效调动学生的思维积极性,引导他们思考如何比较物品的价格高低,即比较商品的单价,进而引出单价这一概念。
(2)带领学生共同探索单价的定义,让学生理解单价的概念,并鼓励他们举例说出日常生活中常见的商品单价,以此进一步理解单价的含义。然后通过10元/个和10元/斤的例子让学生了解商品的单价包含了两部分信息,即价格,以及与此价格相对应的数量,让学生对单价的理解更为深刻。
(3)在以往的教学过程中,学生对于总价的求得已经有了一定的了解,此处先利用买运动衫的案例调动学生脑海中关于总价的记忆,让其产生初步感知,然后再借助买雪碧的案例让学生感知数量增多的同时总价也在变化,从而引导他们掌握单价、数量、总价之间的关系,明白每件商品的价钱与数量相乘就是需要花的钱数,形成“单价×数量=总价”这一数学模型。进而引导他们仔细观察,发现这三者间的变化关系,将函数思想自然渗透进来,使其对该模型的体验更为立体、丰盈。
(4)习题与习题之间是相互承接的,且难度逐次加大。习题依循基础题(夯实数量关系,即总价=单价×数量)→开放题(单价已知,根据对应的数量求总价,以此加深学生对数学模型的理解)→综合题(引出数量=总价÷单价,单价=总价÷数量)的顺序安排。由上可知,教师借助知识与概念的逐一深化,加深了学生对“单价、数量、总价”三者之间的各类数量关系的理解程度。
(三)课例思考策略分析
数学与日常生活是息息相关的,在数学课堂上,怎样引导学生将生活与学习联系起来,让他们学会将现实问题延伸至数学模型的层面,从而培养其数学建模思维和能力是值得数学教师深思的话题,也是提升数学这一学科育人功能的关键所在。
1.营造多样化的真实教学情境,发挥数学的实际价值
一般而言,不同的教学情境能够从不同的维度调动学生的知识库,从多方面启迪他们的智慧,有助于活跃课堂气氛,引发学生更为深入的思考和更为激烈的探讨,从而加深他们对知识的理解和记忆。因此,在教学中,数学教师应掌握营造教学情境的技巧,尽可能营造丰富、有趣的真实教学情境,引导学生合理运用数学思维解决各类现实问题,逐步构建相关的数学模型思想。简言之,数学教师在教学中可以依照如下路径组织教学实践:从现实生活或具体情境中抽象出数学问题→用数学符号建立起相应的数量关系和变化规律→形成对应的数学模型思想,而以上这一路径的实现前提是教师营造多样化的教学情境,借以引导学生发现、提出以及解决现实问题。
2.设计反思应用题型,熟悉模型的运用
教师之所以要培养学生的数学建模意识,归根结底是为了让其学会运用。因此,在具体的教学活动中,教师不仅要关注学生的模型构建过程,也要关注他们的模型构建结果。基于此,教师可以设计一些反思应用题型,让学生在解答同类题型的过程中分析该类题型与数学模型之间的关系,从而明确该数学模型的运用范畴、运用规律以及运用价值等。
