五、数形结合思想
（一）对数形结合思想的认识
数形结合思想，指借助数和形的相应关系来解决数学问题的思路。数和形是对立统一的关系，在一定条件下能够相互转化，从而将复杂的问题简单化。“数”指代数式、方程、函数等；“形”指几何图形和函数图像。直角坐标系与几何图形的结合，用量化的代数运算方式研究图形的性质，典型的就是数形结合思想的运用。
数形结合思想的核心在于将代数与几何有机结合起来，以更好地分析数学难题。比如在解决不等式和函数问题中，使用图像的方法能够直观厘清其中的关系，采用数形结合的方式需要把握恰当的时机。
数形结合思想和几何直观，是相互联系又存在区别的。数形结合思想包含“以形解数”和“以数解形”两种思路。几何直观，指借助图形来分析数学问题，比如通过观察图形的运动理解几何图形。
数形结合思想能够将抽象、复杂的问题具体化、简单化，利用形象思维解决数学难题，优化解题的思路。在小学数学教学过程中，考虑到小学生的逻辑思维尚处于较低的水平，采用数形结合的方法将数学知识进行直观化，有助于小学生更好地理解问题，树立数形结合思想。
（二）数形结合思想的应用
数形结合思想在数学中的应用通常有两种方式，一种是利用数的明确性和可操作性来揭示图形的性质，另一种是借助几何图形来阐述概念与数之间的关系，这一思想的应用具体表现在以下几个方面。
（1）实数与数轴上的点的对应关系；（2）函数与图像的对应关系；（3）曲线与方程的对应关系；（4）与几何有关的数学知识，比如三角函数；（5）概率统计的图形表示；（6）在数轴上表示不等式的解集；（7）数量关系式的几何意义，比如s=10t。
在小学数学阶段，数形结合思想能够通过“形”来简化数学问题，比如数轴和直角坐标系中正反比例关系图、数轴，还有统计图形和几何概念模型等都是数形结合思想的具体表现，能够很好地帮助学生感受代数和几何的魅力，从中加深学生对数形结合思想的理解。
（三）数形结合思想的教学
1.正确理解数形结合思想
小学数学教师在教学过程中，需要经常性地利用直观的模型图来帮助小学生理解数学问题，从而使学生更好地把握数形结合思想的本质。比如使用数轴、线段图、图形等来分析数、数量关系，达到“以形解数”和“以数析形”的良好教学效果。
2.拓展数形结合思想的应用
在小学阶段，数形结合思想的应用常见的有计算图形的周长、面积和体积等。教师应当对数形结合思想加以拓展，帮助小学生在现有知识的基础上进行开拓，锻炼其“以形解数”的能力。
案例：用两个完全相同的直角三角形和一个等腰直角三角形（等腰直角三角形的腰等于直角三角形的斜边），拼成图4-11的直角梯形。试分析每个直角三角形的两条直角的边的平方的和与斜边的平方之间的关系。
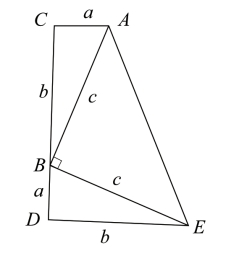
图4-11
分析：设直角三角形的两条直角边各为a、b，斜边为c，可知等腰直角三角形的直角边为c，且三个三角形的面积和等于直角梯形的面积。
根据三角形面积公式：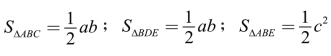
，则三个三角形的面积和为：
。
根据梯形的面积公式，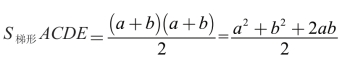
。
由于三个三角形的面积和与直角梯形的面积相等，所以：
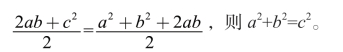
由此可见，直角三角形的两条直角边的平方和等于斜边的平方，这就是著名的“勾股定理”。