稳定电流场的性质

一、稳定电流场的性质

1.电流密度与电场强度的正比性

这便是稳定电流场中的欧姆定律。这个公式既适用均匀介质，也适用于非均匀介质。因为在介质不均匀的情况下，我们总能选取一个足够小的体积元，将其电阻率看作是均匀的。式（1-5）又称为欧姆定律的微分形式。

2.稳定电流的连续性

在稳定电流场中，虽然有电荷的运动，但那只是空间点上一些电荷元被另一些电荷元所代替，而该点的电荷密度仍保持不变。稳定电流场中的电流满足电量守恒定律，它表明除去电源点外，流入流出任一包围电流源的闭合曲面S的电流的代数和为零，电流密度既不可能增加，也不能减小。一般情况下，电流密度的法向分量Jn沿任一闭合曲面S的积分应该等于零，即

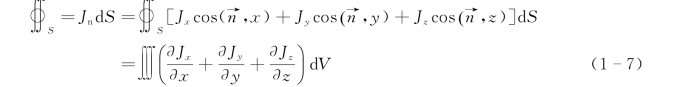
于是，结合式（1-6）及式（1-7）有

这就是电流连续性的微分表达式。它表示电流密度矢量沿直角坐标系的三个方向的空间变化率的总和为零。即在稳定电流场中，电流线是连续的，除电源点外，空间任何点上不会有正电荷或负电荷的积累。

3.稳定电流场的势场性

从稳定电流场的上述性质可知，电流在空间的分布是稳定的，即不随时间而变化，它和静电场一样是一种势场。场内任一点（除场源外）的电位U与场强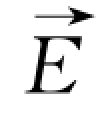有如下关系：

式（1-9）说明空间某点的电场强度等于电位的负梯度。在极坐标系中，式（1-9）可写成

在直角坐标系中，场强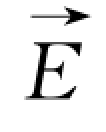沿x轴、y轴、z轴三个方向的分量分别为

于是场强和电位梯度可分别写成

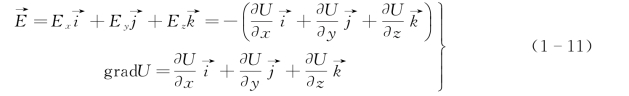
综上所述，若将欧姆定律的微分形式及电位梯度的表达式代入电流密度连续方程式（1-8）中，则由于

便可得到均匀介质中的电位方程

式（1-12）称为拉普拉斯方程，解此方程即可求出稳定电流场的电位分布。