反射波、透射波和折射波的形成
1.反射波的形成
每一介质的密度ρ与波在介质中传播的纵波速度V的乘积，称为波阻抗或声阻抗。当地震波垂直入射到波阻抗不同的介质分界面上时，其能量要重新分配。一部分能量穿过界面继续向前传播，称为透射波；而另一部分反射回去，称为反射波。由于垂直入射时，不存在沿界面方向的振动分量，故入射波、反射波、透射波都沿界面的法线方向传播。设入射波的振幅为Ai、反射波的振幅为AR，反射波和入射波振幅之比，称反射界面的反射系数R。当波垂直入射到界面上时，R为
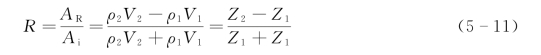
式（5-11）中，Z1=ρ1V1，Z2=ρ2V2，表示界面上下两种介质的波阻抗。
多层介质时的反射系数一般式为
由反射系数可知，当R=0，即Zn=Zn-1时，这实际上是一种均匀介质，不存在分界面，不产生波的反射。只有当Zn≠Zn-1，即R≠0时，才能形成反射波。Zn与Zn-1的差别越大，R越大，反射波越强。R的值域为-1≤R＜1。当Zn＞Zn-1时，R＞0，反射波与入射波的相位相同，都为正极性；当Zn＜Zn-1时，R＜0反射波为负极性，它与入射波的相位相反，相差180°，这种现象称为半波损失。
当地震波以某个入射角α射到介质分界面时，它的一部分能量经界面反射，以α＇角（反射角）出射形成反射波，另一部分能量则透过界面，以β角折射至下一个岩层，形成透射波，β称为折射角，如图5-9所示。
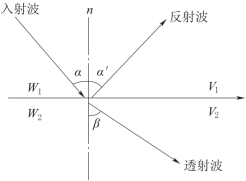
图5-9 反射波和透射波的形成
入射线、反射线、透射线和界面法线同在一个平面内，此平面叫射线平面，它和弹性分界面垂直。这时，入射线、反射线位于反射界面法线的两侧，入射角α等于反射角α＇，这就是反射定律。
2.透射波的形成
当入射波透过反射界面形成透射波时，由于分界面两侧介质波速的不同，透射波的射线要改变入射波射线的方向，而发生射线偏折现象。偏折程度的大小决定于透射定律：入射线、透射线和界面法线在同一射线平面内，入射线、透射线位于法线的两侧；入射角α的正弦和透射角β的正弦之比等于入射波和透射波速度之比，或者说入射角、反射角和透射角的正弦和它们各自相应的波速的比值等于一常数（图5-10）。这个定律亦称为斯奈尔定律。
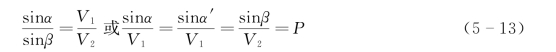
由式（5-13）可知，当V1＞V2时，α＞β，透射波射线靠近法线偏折；当V1＜V2时，β＞α，透射波射线远离法线，而向界面靠拢；在多层介质中，假定速度是递增的，透射波射线则是一条折线。
设透射波的振幅为At，入射波振幅为Ai，则透射系数T为
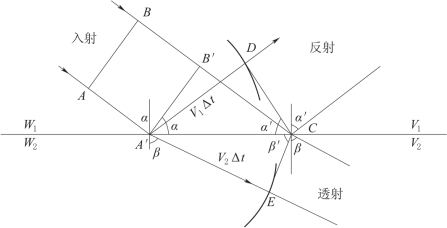
图5-10 反射角透射角与入射角的关系
根据理论证明，当波垂直入射时，透射系数为
根据反射和透射系数的公式，可得
从透射系数的定义知道，T的值域为0≤T＜2，一般的沉积岩层，R约为0.2，所以，只要T≠0，总可以形成透射波；两种介质的R越小，透射系数越大，透射波越强（反射波越弱），反之，R越大，T越小，折射波就弱（反射波就强）；无论Z2＞Z1或Z2＜Z1，T总是正值，透射波和入射波相位一致，透射波极性为正极性。
3.折射波的形成
假设地下有一个水平的速度分界面，且下面介质的传播速度V2大于上覆介质的速度V1，从震源发出的入射波以不同的入射角投射到界面上，依据斯奈尔定律，随着入射角α的增大，透射角β也随着增大，透射波射线偏离法线向界面靠拢，当α增大到某一角度i时，可使β=90°。这时透射波就以V2的速度沿着界面滑行，形成滑行波，这时的入射角i称为临界角，即
由波前原理知道，高速滑行波所经过的界面上的任何一点，都可看作从该时刻振动的新点源，因此紧邻介质中的质点就要发生振动。由于界面两侧介质质点存在着弹性联系，因此下面的质点振动必然要引起上覆介质质点的振动，这样在上层介质中就形成了一种新的波动，这种波动的传播，就形成折射波，如图5-11所示。
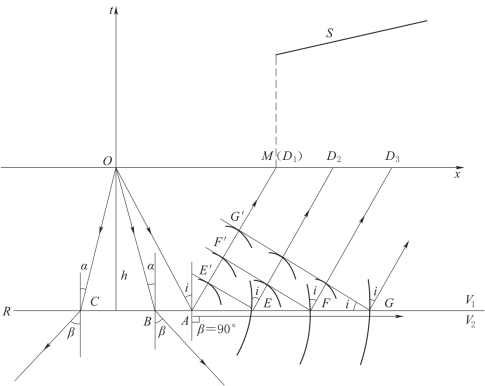
图5-11 折射波的形成
折射波的射线是垂直于波前GG＇的一簇平行直线，射线AM是折射波的第一条射线，在地面上从M点开始才能观测到折射波，所以称M点为折射波的始点。自震源O到M点的范围内不存在折射波，故称该范围为折射波的盲区，盲区的半径XM为
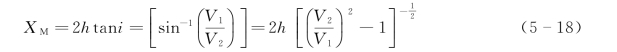
由斯奈尔定律可知，要在某一地层顶界面形成折射波，必须是该层波速大于上覆所有各层介质的速度。如果上、下地层速度倒转，即中间出现速度相对较低的地层，在这界面顶面就不能形成折射波。