井间弹性波CT的资料处理
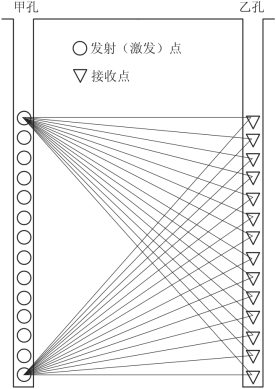
图8-24 钻孔地震CT层析成像观测系统示意图
井间弹性波层析成像资料的处理分为两部分：射线追踪和反演成像。
（一）理论基础
井间弹性波层析成像中，弹性波射线走时可以表示为慢度（速度的倒数）沿射线的积分，即
式中：W为慢度；x为目标区点的坐标；s、r分别为震源和接收点；l为射线路径；δT为噪声。
令limk→∞Wk（x）=W（x），得
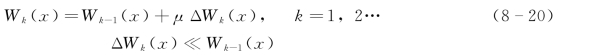
式中：ΔWk为慢度扰动量；μ为松弛因子；k为迭代次数。
则
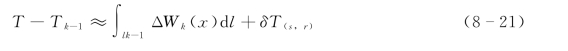
式（8-21）也可表示为
式中：Ak-1为射线段长度组成的系数矩阵；ΔTk为走时差，ek为观测值差。
在已知初始慢度W0的情况下，通过射线追踪求出Ak-1和ΔTk。以此为基础，由迭代计算可以获得慢度W（x）的解。
在研究区进行CT成像之前，需要对成像区和式（8-19）离散化，即
式中：Ti为记录的走时数据；Wj为第j个离散单元内的平均慢度；lij为第i条射线经过第j个离散单元内的射线长度；m为离散单元个数。
式（8-23）可以写成线性代数方程：
式中：A为n×m阶矩阵，其元素aij（i=1，2，…，n；j=1，2，…，m）是第j个单元慢度Sj对第i个走时ti（观测值）的贡献量，aij=lij，n为射线路径（或接收点）个数；X为待求的离散单元慢度值的向量，X=（X1，X2，…，Xm）T；b为各射线走时，bi=ti。
需要说明的是，当介质速度变化不大时，弹性波射线可以近似认为是从激发点到接收点的直射线。对于复杂模型介质，其速度变化大，弹性波射线轨迹通常为弯曲的。这时，弯曲射线追踪比较困难，主要方法有打靶法、最小走时法、线性走时插值法、平方慢度法、有限差分法等。此外，通过各接收点记录的走时重构井间模型参数（慢度）的反演方法也有很多，譬如最小二乘法（LSQR）、共轭梯度法（CG）、代数重构法（ART）、联合迭代算法（SIRT）和奇异值分解法（SVD）等。
（二）资料处理流程
（1）在成像计算时必须知道首波（初至波）从激发点到接收所走路径，当所测剖面比较均匀时可近似为两点间连线（直射线）。当异常体变化很大时，根据费马原理首波将沿走时最小的路径传播，要实现弯曲射线CT首先必须能够快速计算出首波走时和路径，通过应用《图论》中Dijkstra所提出的最佳路径算法，成功解决了这一难题[2，3]，使得计算次数由O（N1）降为O（N2）。同时通过限定射线弯曲程度减少查找结点数可以进一步提高成像速度。
（2）在首先使用直射线方法对剖面成像后，剖面速度图像由许多正方形单元组成，每个单元内波速可近似认为均匀不变。据弹性波传播原理射线只能在单元边界上发生反射、折射或散射，因此进行射线追踪时，首先要对单元边界进行离散，选择快速计算方法是只用边界交点作为计算结点；精细计算方法是在单元边界中间内插一个结点，这样精度有所提高，但计算时间加长。由于弯曲射线是在直射线附近弯曲，如果用剖面内所有结点来追踪射线，计算量很大且没有必要。因此，规定在进行射线追踪时，在以其激发点和接收点作为焦点所作椭圆内进行，则结点数可减少很多，提高计算速度。当椭圆参数b/c=1/10时称为小弯曲成像方法，适用于异常体较小的情况；当椭圆参数b/c=1/5时称为大弯曲成像方法，适用于异常较大的情况。
