二层介质的折射波时距曲线
(一)二层水平界面的折射波时距曲线
假设地面下深度为h处有一水平的速度分界面R,其上、下层的速度分别为V1和V2,且满足V1<V2的条件(图6-1)。震源点为O,通过O点布置测线Ox,在测线上的x1、x2、x3、…、xn等点上分别安置检波器接收地震波信号。在OM段内,检波器首先接收到的是直达波。直达波从震源O点出发,沿测线x传播到任意点的旅行时间t为
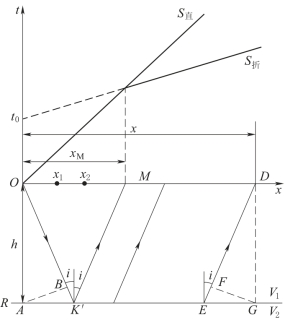
图6-1 水平二层介质折射波时距曲线
![]()
式(6-1)就是直达波的时距方程。通常以震源点的距离x为横坐标,地震波旅行时t为纵坐标,便可作出相应的时距曲线。显然,由式(6-1)可知,直达波的时距曲线为一直线方程。由此,得到了两支通过原点O且对称于t轴的两条直线。对折射波曲线,为方便起见,只研究Ox轴右边的一支曲线(左边完全和右边对称)。
如前所述,当入射波的入射角达到临界角i时,才开始产生滑行波,即只有满足x>xM条件的检波器才能接收到折射波。设有一检波器安置在测线D处,其炮检(即震源与检波器之间的距离)为x,则折射波的旅行路线为OKED,它的旅行时间t为
![]()
从A、G分别作OK、ED的垂线AB和GF,由几何关系得到∠BAK=∠EGF=i。

这就是水平二层介质的时距方程。可见它的时距曲线也是一条直线,这条直线的斜率为1/V2,直线S折延长与t轴相交于t0,截距时间t0为
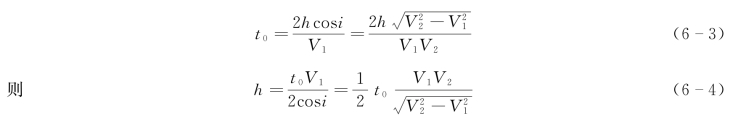
由此可见,可以利用直达波时距曲线求出V1,利用折射波时距曲线求出V2和截距时间t0,即可按上述公式计算出震源点(即炮点)下界面的埋藏深度h。
这时,折射波盲区的半径为
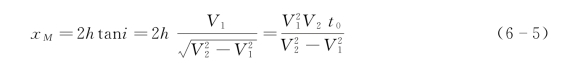
当x<xM时,无折射波出现;当x>xM时,有折射波。但在此范围内,同样还会出现直达波、反射波(包括多次反射波);这样就有可能造成这些波的相互干涉和叠加。
(二)二层倾斜界面的折射波时距曲线
1.时距方程
如图6-2所示,R为一倾斜折射界面,V2>V1。当在炮点的下倾方向接收折射波时,波沿射线的走时t下为
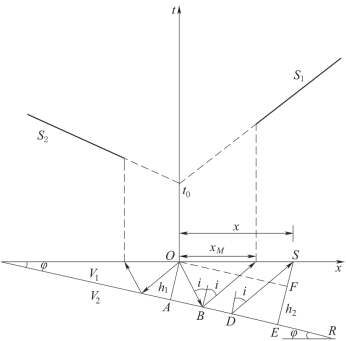
图6-2 倾斜平界面时距曲线
![]()
通过几何换算可以推出时距方程t下的表达式:
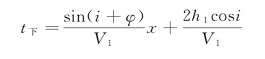
同理可推出炮点上倾方向接受到的折射波时距方程为
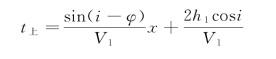
合并上面两式,即可得到倾斜界面的折射波时距方程的一般式:
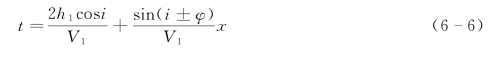 (https://www.daowen.com)
(https://www.daowen.com)
2.时距曲线特点

两条时距曲线的斜率的倒数或视速度的倒数分别为

分析式(6-7)、式(6-8)可知,下倾方向时距曲线的斜率较大,视速度小,曲线陡;上倾方向折射波的斜率小,视速度大,曲线较平缓。因此,通常可以从这两条时距曲线的陡缓情况定性判断其折射界面的倾斜方向。
对式(6-7)、式(6-8)进行变换,可得到
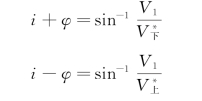
联合两式即得到
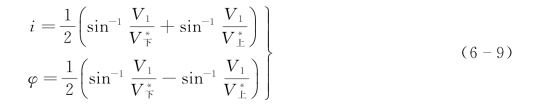
如果V1为己知值(可从直达波资料求取),并从折射波时距曲线上分别求得两条曲线的视速度,便可用式(6-9)求取折射波临界角i和界面的倾角φ。由临界角i和V1又能求出界面速度V2。
倾斜界面的折射波时距曲线存在盲区的临界值分别是
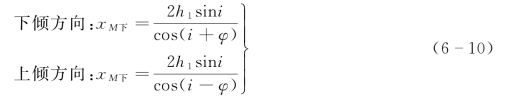
显然,整个盲区的半径即为
![]()
在进行地震勘探时,对倾斜界面的倾角有下列要求,即应满足i+φ<90°。因为当i+φ>90°时,若在下倾方向观测,则折射波不能到达地面接收点;若在上倾方向观测,则入射角总是小于临界角,而不能产生折射波(图6-3)。因此,在大倾角地区进行折射波观测时应注意这一条件。
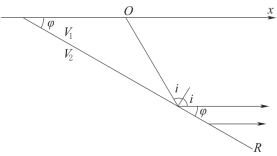
图6-3 i+φ=90°的情况
(三)弯曲界面的折射波时距曲线
通常界面总有不同程度的弯曲。弯曲界面上折射波时距曲线不是直线,而是呈曲线形状。当折射界面为凸形时,其时距曲线如图6-4所示,即呈向上弯曲的凹曲线。反之,如果折射界面为凹形时,其时距曲线如图6-5所示,呈向下弯曲的凸曲线。
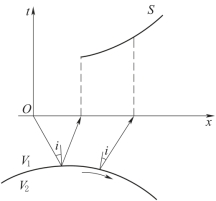
图6-4 凸界面情况时距曲线
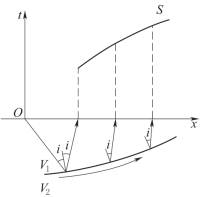
图6-5 凹界面情况时距曲线
随着凸界面曲率半径的减小,波将出现一个特殊现象,即穿透现象,便无法得到真实的时距曲线,从而为野外勘探带来困难。为了及时发现穿透现象,在野外工作时,应该在接收地段的同侧,在不同的位置激发震源,以对同一地段进行重复观测。这种情况下所得到的时距曲线即称为追逐时距曲线。如果存在穿透现象,则由于传播路径和方向的变化,时距曲线的平行性受到破坏,如图6-6所示。如果没有穿透现象,则所得两条时距曲线是相互平行的,如图6-7所示。
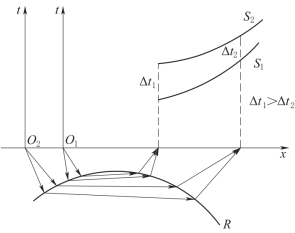
图6-6 穿透现象情况时距曲线
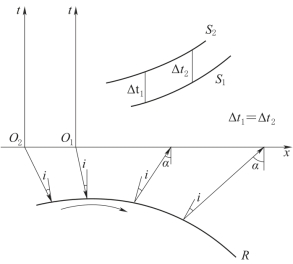
图6-7 未穿透现象情况时距曲线
