瑞雷面波的形成及特征
面波的形成可以用一个简单的例子来说明，图8-33是一个地表下厚度为H的覆盖层的简单模型。如果一平面体波的简谐波在图中覆盖层内的传播满足全反射条件，其传播的射线路径为ABCDEF，则根据波前面与射线垂直的性质，虚线CF可以代表波由C、D、E和F经过两次反射后到达F的波前面，也可以表示由A传播到C的后续振动的波阵面。当波前面与波阵面的时程差CDEF正好等于波长的整数倍，则两者完全同相位，其合成或叠加属于相长干涉，并且形成一种沿着层间行进的次生表面波，这种波的能量更强且能量主要集中在地表附近。瑞雷面波的形成可以用波动理论做更严谨的推导。
瑞雷面波的传播特征可以分为以下四个方面。
（一）位移特征
波动方程中的P波和S波可以用位函数φ和ψ表示。对于简谐波φ和ψ具有eiωt的形式。如果存在由P波和S波叠加形成的瑞雷面波，则φ和ψ满足波动方程的解可以表示为
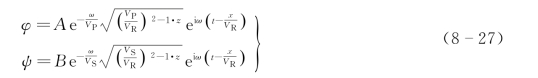
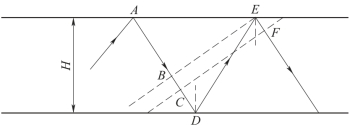
图8-33 面波的形成
式中：VP、VS和VR分别为纵波、横波和面波波速；ω为简谐波的角频率；x为地表距离；z为深度；t为波的传播时间；A、B为系数，可以通过引入边界条件获得。
把式（8-27）中的位函数代入位移分量中，求偏导数后令z=0，即可得到地表处质点在x和z方向上的位移分量：
式中：c为任意常数，与震源强度和介质吸收特性有关。
从式（8-28）可以看出，地表处质点位移的水平分量与垂直分量的幅值之比为2∶3，且水平分量的相位滞后π/2，因而质点位移呈绕其平衡位置的椭圆，在平衡位置正上方时质点运动方向与波的传播方向相反，故而可以将面波质点运动轨迹称为逆进椭圆。
此外，式（8-27）中位函数φ和ψ的幅值随深度z增加按指数迅速衰减，一般认为瑞雷面波的影响深度（或穿透深度）不超过一个波长的值。
（二）波速特征
波速是反映介质性质的重要参数，它是瑞雷面波勘探的基础，由介质的弹性模量和泊松比ν之间的换算关系，以及瑞雷面波在介质中的传播特点和条件方程（或频散方程），可以得到瑞雷面波波速与横波波速之间的近似关系为
工程勘察中，一般土层的泊松比ν=0.45～0.49，于是VR≈0.95VS。为此，在难以获得介质横波波速的地区，可以通过测量瑞雷面波波速，估算有关介质的横波波速以及相对应的岩土力学参数。
在自由表面的瑞雷面波形成的讨论中，地下介质被认为是一个均匀、无限大的半空间。实际上，由于瑞雷面波的穿透深度大约为一个波长，在地表测得的瑞雷面波速度被认为反映了小于一个波长的某一深度范围内介质的平均弹性性质。为此，实际测量时可以激发不同频率的瑞雷面波（其波长也随之变化），可以获得反映不同深度范围内介质的平均速度，这是面波勘探资料处理解释的依据之一。
（三）衰减特征
P波和S波的波前在均匀介质中为球面，其能量按1/r2的规律衰减（r为震源与接收点之间的距离），也就是说波的振幅以1/r的方式减小。瑞雷面波的波前在介质内是高度约为一个波长的圆柱面，为此，波的能量按源距r的倒数形式衰减，即瑞雷面波的振幅按1/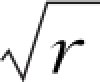
的规律减小。这表明，瑞雷面波比体波的衰减慢得多，这也是面波勘探的优势之一。
（四）频散特征
实际介质中传播的波动很少为单频波，往往是由许多不同频率的单频波叠加而成的复合波。其中，每个单频波的传播速度称为相速度V，复合波的传播速度称为群速度U，二者之间的关系为
式中：λ为单频波的波长。
当波动的相速度随着频率而发生变化，则该波动有频散现象。在弹性介质中，体波的各相速度与频率无关，U=V，即没有频散现象，实际中体波可以表现为弱频散现象。然而，面波在传播中有频散现象，这将给资料分析带来困难。当相速度随频率的降低而增大时属于正频散（U＜V），反之为反频散（U＞V）。
自由表面的瑞雷面波是面波中的一个特例，它的频散方程中不包含频率参数，表明其相速度与频率无关，即无频散现象。