电测深曲线的定量解释

三、电测深曲线的定量解释

电测深曲线定量解释的目的是在定性解释的基础上确定各电性层的埋深、厚度和电阻率的具体数值，绘制各种定量解释图件。定量解释的方法很多，主要有三类：量板法、简捷定量法、数值解法。

量板法就是运用理论曲线与实测电测深曲线进行对比求解的方法。在已知水平层状地电断面中各层厚度和电阻率的情况下，根据电测深的理论公式计算并绘出许多理论曲线，将其按层数和地电断面类型分类组成的曲线图册称为量板，目前常用的有二层量板、三层量板和辅助量板。

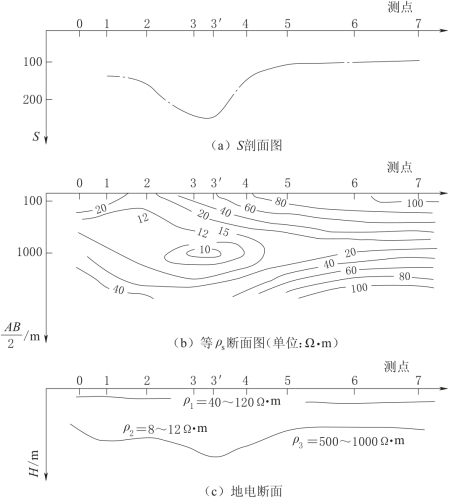
图2-57　某地电测深综合剖面图

对于水平层状断面且电性层数有限的电测深曲线，用量板法对二层或三层断面的电测深曲线进行定量解释，其成果的准确程度较高，但对四层或更多层的曲线作定量解释时，其成果的误差较大。

对每个测点的电测深曲线作定量解释后，可求出各电性层的埋深、厚度和电阻率值。根据各个测点上电测探曲线定量解释的成果，对每条测线可以绘出地电断面图，如能对比其中各层的电性与岩性，就可以绘出电性-地质剖面图。对全测区，可绘制电性层顶板等高线图、某一电性层的等厚度图、电性-地质平面图。这些图件是电测深工作的主要图件。

1.二层量板及二层曲线的解释

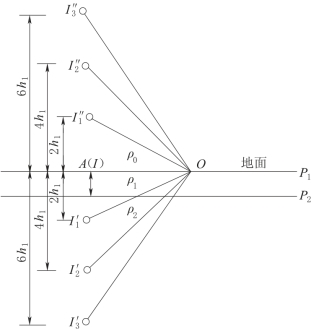
图2-58　用镜像法求解水平二层断面地表的电位

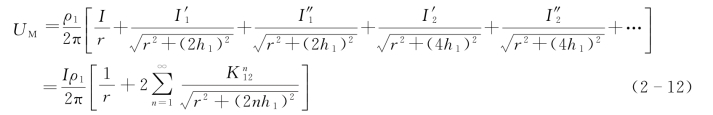
于是可求出该点的电场强度E和视电阻率ρs：

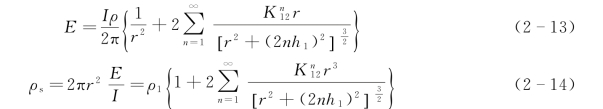
这就是水平二层断面电阻率测深理论曲线方程。当断面中ρ1、ρ2、h1各参数已知时，代入式（2-14）即可算出随r而变化的二层测深曲线。若将不同断面参数所算出的许多理论曲线绘于一张图纸上，即构成水平二层电测深曲线量板。但是，实际的地电断面结构和各层的电阻率因地而异，变化万千。绘制量板时又不可能包罗万象地绘出全部参数的任意值的理论曲线。为了解决这个矛盾，既减少理论曲线的数目，又便于实际应用，在作量板时采取了如下两个措施。

一个措施是：理论曲线方程中有关电阻率的各项均以ρ1为单位，有关距离的各项均以h1为单位。这样，若以函数形式表达，式（2-14）可写成ρs=f（ρ1，ρ2，h1，r），转换为

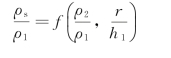
实际用于计算的方程为

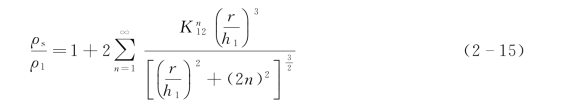
理论曲线绘于双对数坐标中时为

实测曲线绘于双对数坐标轴中时为

两者在双对数坐标中的差别仅仅是曲线的纵坐标位移lgρ1，横坐标位移lgh1，而它们的形状是完全相同的。这样不仅便于对比，而且由对比后理论曲线与实测曲线横坐标的位移量确定h1值。

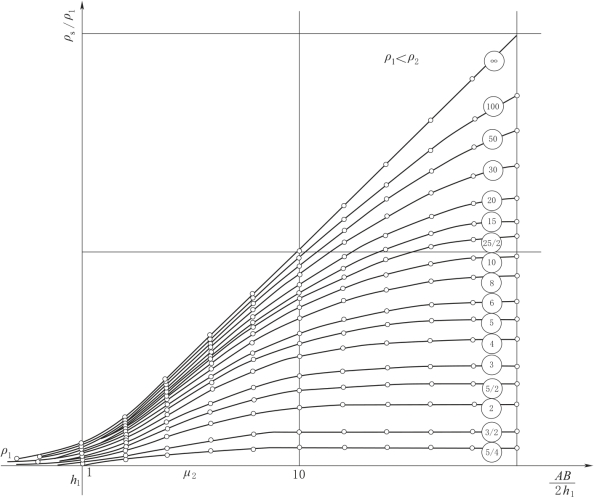
图2-59　水平二层G型量板

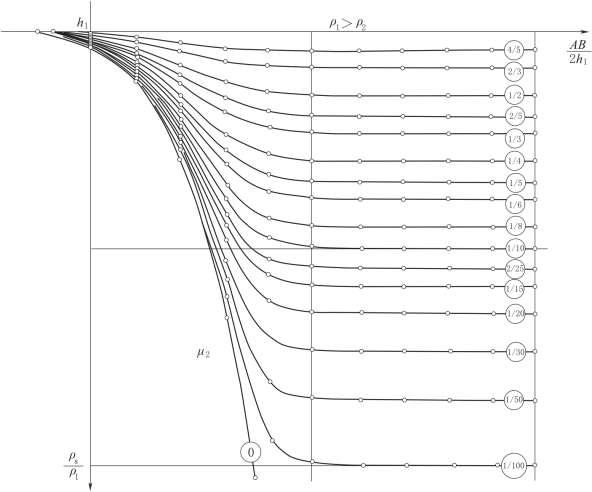
图2-60　水平二层D型量板

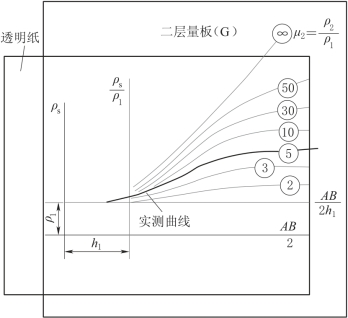
图2-61　用量板解释二层曲线灰线—理论曲线；黑线—实测曲线

当实测曲线均匀分布于两条理论曲线之间时，则需按对数坐标规律进行内插求得μ2值，而不能按算术坐标规律内插。

2.三层量板及三层曲线的解释

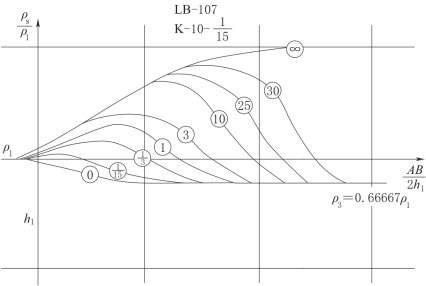
图2-62　K型三层量板

三层曲线解释的目的是求出各层的电阻率及一、二层的厚度。现结合一条实测H型曲线来说明用三层量板解释三层曲线的步骤。

（1）确定ρ2值，最好用电测井资料确定ρ2值，或是通过对岩石露头、岩石标本实测确定。本例中已给出ρ2=9Ω·m。

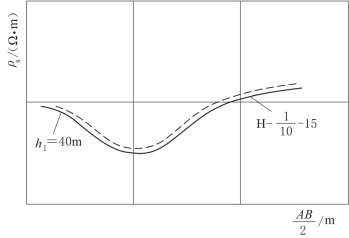
图2-63　三层曲线解释实例

（3）将实测曲线与量板对比，求出h1和h2值。在保证实测曲线与量板两者纵横坐标轴都彼此平行的条件下，上下左右移动透明纸（实测曲线），找出与实测曲线重合最好的理论曲线（可以内插），并记下其参数ν2=3。这时量板坐标原点在实测曲线横坐标的对应位置即为h1=40m，于是可求出h2=ν2h1=120m。

（4）等价校正，当所选用的量板与实测曲线的μ2、μ3都一致时，按上述方法求出的h2即为第二层的真实厚度，否则应做等价校正。

对于H型和A型断面，其属于S2等价性质，校正公式为

对于K型和Q型断面，其属于T2等价性质，校正公式为

3.辅助量板及其应用

借助于二层量板和辅助量板可以对三层或三层以上的多层曲线进行解释，步骤简便，是野外常用的解释方法。

（2）辅助量板的编制。为了使用方便，由经验公式计算出代替层点坐标，获得其与参数μ2、ν2的关系曲线，绘成列线图，称为辅助量板，有H型、KM型、AM型、Q型辅助量板。

现以H型断面为例说明这种量板的编制方法。H型断面代替层的参数经验公式为

绘制辅助量板时，仍以h1和ρ1为单位，式（2-20）变为

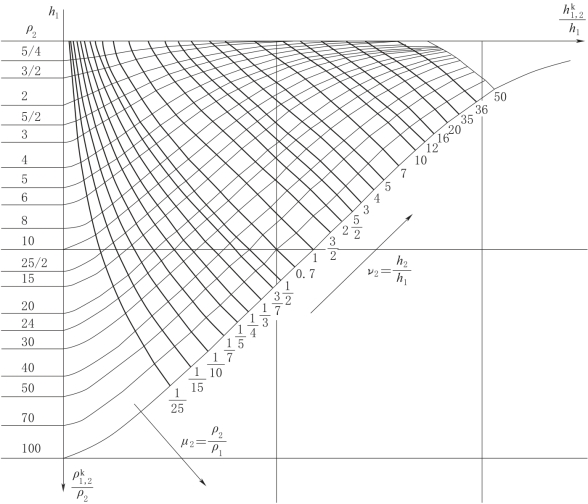
图2-64　对称电测深KM型辅助量极

（3）用辅助量板和二层量板解释二层曲线。现结合实例说明解释步骤。有一K型曲线，已知ρ2=100Ω·m，求解ρ1、h1、h2、ρ3四个参数。

1）用二层量板求ρ1、h1，选用G型量板，求出量板原点在实测曲线上的位置O1点，于是得ρ1=20Ω·m，h1=4m[图2-65（a）]。

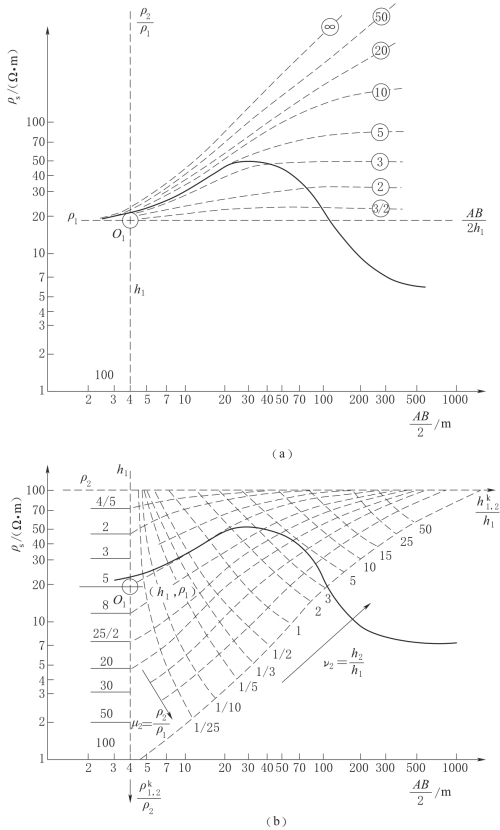
图2-65（一） 用辅助量板解释三层曲线

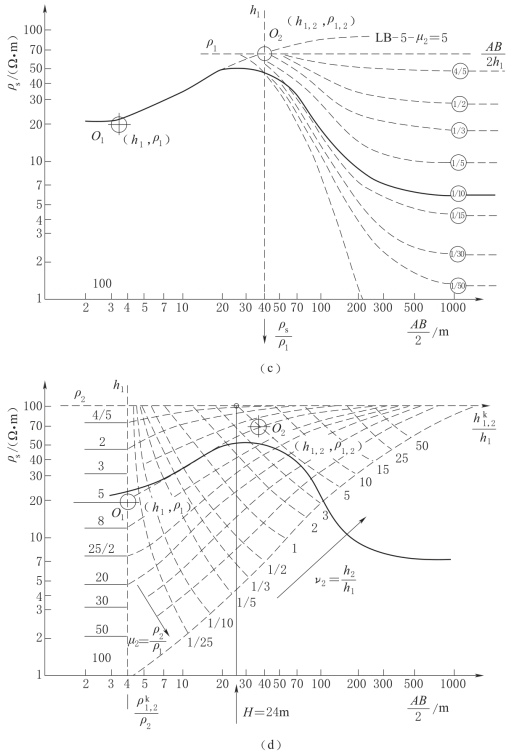
图2-65（二） 用辅助量板解释三层曲线

（4）用辅助量板和二层量板解释多层曲线。解释多层曲线，同样要在已知中间层参数ρ2、ρ3的条件下进行。解释四层曲线前段时，暂忽略第四层的影响，把前段当作三层曲线，并运用上述步骤进行解释，求得前三层的所有参数。然后，把四层曲线的后段看作是由第一、二、三层组成的代替层（h1，2，3，ρ1，2，3）与第四层组成的新二层断面，求解h3和ρ4。

4.量板法解释结果的综合改正

用量板法解释电测深曲线，应该满足的前提条件是：①地形平坦；②岩层倾角小于20°；③各层的电阻率均匀且各向同性；④已知可靠的中间层电阻率参数；⑤电测深曲线完整，质量可靠。若不能满足上述条件，解释结果与实际情况有误差，要进行综合改正。所谓综合改正就是将井旁测深曲线的解释结果与该井地层柱状图反映的各岩层的深度进行对比，将曲线解释的结果改正到岩层的真正深度上去。具体作法就是用钻井中岩层的实际深度与井旁测深曲线解释深度的比值作为综合改正系数，然后将测区中其余测点（未知点）的曲线解释结果乘以综合改正系数即可。

5.简捷定量法

水平二层断面中，当ρ2→∞时，其尾部渐近线方程为

式中：S1为第一层的纵向电导率。

若令此渐近线与ρ1=1的水平线相交，则由于该水平线的方程式为lgρs=0，于是两式联解可得

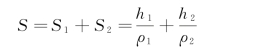
于是可得

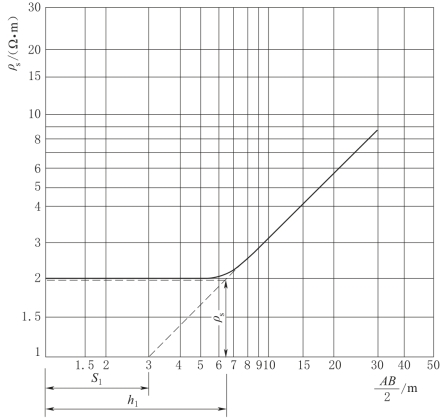
图2-66　用S法求h1

当测区上覆地层的纵向电阻率比较稳定时，就能利用S判断基底的起伏情况。如果测区有钻孔资料，则可以知道H=h1+h2+…+hn-1，由孔旁测深曲线图解求得S，则ρt=H/S。若测区内钻孔较多，则可求出上覆n-1个岩层的平均纵向电阻率值。待解释的各测点只要分别量出各自的S值后，便可反求出各测点的基岩埋深H值：

有了S值，可绘制S值平面等值线图、基岩埋深平面等值线图，也可以绘制S剖面图表示基底的起伏情况。

亦可写成差商形式：

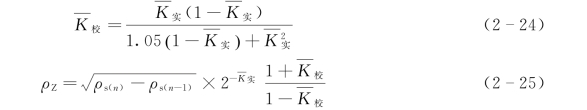
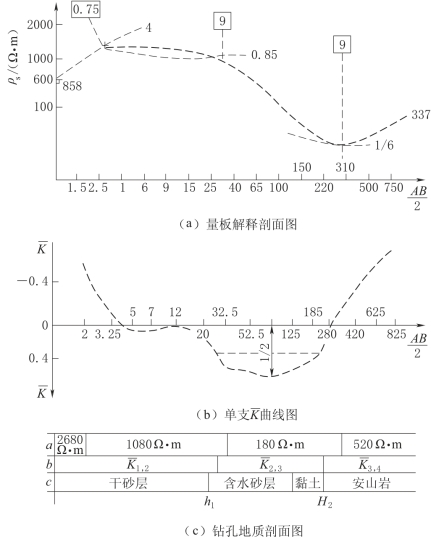
图2-67　1124号孔ρs和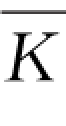曲线图

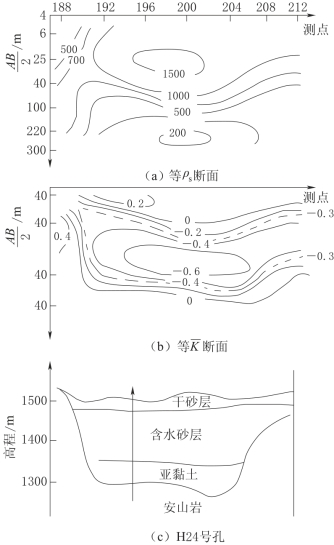
图2-68　元一180号剖面综合地电断面图

（3）电测深曲线的数字解释法。用电子计算机对水平层电测深曲线进行数字解释已有很大发展，现已建立了多种解释方法。目前我国采用较多的是最优化分层解释法，就是利用最优化计算方法求取使理论曲线和实测曲线之间拟合差为极小值的电性层参数。在具体做法上又分为两类：一类是把理论曲线视电阻率值与野外实测视电阻率值直接进行比较；另一类是首先从野外视电阻率值导出电阻率转换函数值，然后与理论模型计算出的电阻率转换函数值进行比较。根据需要也可以把这两种方法结合使用[19]。

1）电阻率转换函数。多层水平介质条件下，地面点电流源A的地中电场分布满足拉普拉斯方程。若将坐标原点选在A处，Z轴垂直向下，由于电场分布对Z轴有对称性，与观测点方位角ψ无关，故电位分布满足下面形式的拉普拉斯方程（图2-69）：

图2-69　多层水平地层模型

用分离变量法对式（2-26）求解，得地面上任意点M处的电位表达式：

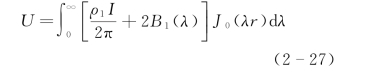
式中：λ为积分变量；J0（λr）dλ为零阶贝塞尔函数；B1（λ）为积分变量λ的函数。

水平二层和三层地电断面的B1（λ）函数分别为

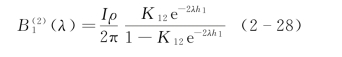
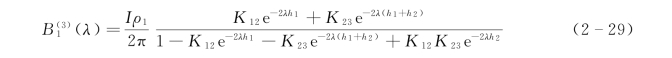
若令式（2-27）中的B1（λ）为

则电位公式变为

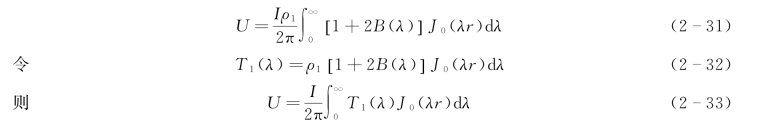
T1（λ）称为电阻率转换函数，是积分变量λ及h1、h2、…、hn-1，ρ1、ρ2、…、ρn的函数。二层和三层断面条件下，地表面的电阻率转换函数为

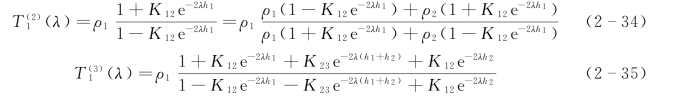
地下存在n层水平介质，若将第n层以上的所有地层去掉，则只剩下电阻率为ρn的一种均匀介质，将得到第n层表面的电阻率转换函数T（n）（λ）ρn。若将第i层以上各层全部去掉，只剩下第i、i+1、i+2、…、n-1，n层时，第i层介质表面的电阻率转换函数为

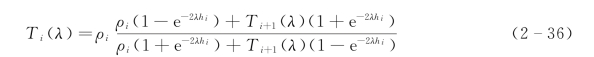
2）视电阻率和电阻率转换函数的褶积表达式。当采用MN→0的梯度装置进行电测深时，视电阻率为

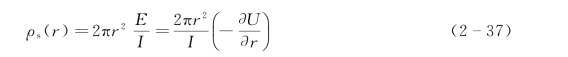
将式（2-33）对r求一阶导数，并考虑贝塞尔函数的微商性质，可得

式中：J1（λr）为一阶贝塞尔函数。

将上式移项，可得

对式（2-39）利用傅里叶-贝塞尔积分的汉克尔逆变换，可求出电阻率转换函数T1（λ）的积分表达式

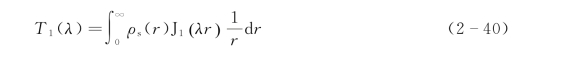
式（2-38）和式（2-40）表明了视电阻率ρs（r）和电阻率转换函数T1（λ）的相互关系。已知ρs（r）可求T1（λ），反之亦然。但是，直接计算两式的积分值是比较困难的。由于电测深曲线通常是对数坐标，如果对ρs（r）和T1（λ）的自变量取对数并作变量代换，令

式（2-38）变成

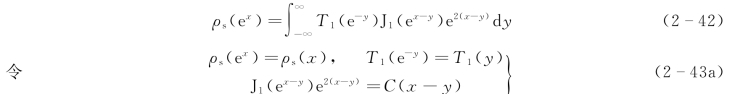
式（2-42）简写为

与式（2-41）作同样的变量代换，式（2-40）变为

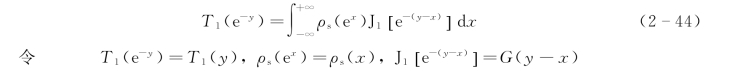
则式（2-44）简化为

式（2-43b）和式（2-45）为视电阻率和电阻率转换函数的褶积表达式。为了能在电子计算机上对式（2-43b）和式（2-45）的积分进行数值运算，必须采用取样的方法，使式中的积分离散化。假设ρs（x）和T1（y）的截止频率为fc[当f≥fc时ρs（x）和T1（y）的振幅均趋于零]，根据取样定理，当取样间隔Δx（或Δy）≤1/2fc时，若以iΔx表示第i个取样点上ρs（x）的自变量值，以jΔy表示第j个取样点上T1（y）的自变量值，ρs（x）和T1（y）两函数离散取样值的取样序列分别为

则两函数离散型的褶积运算表达式为

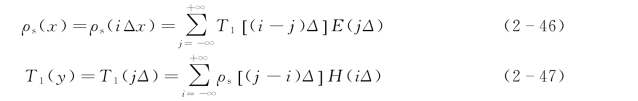
3）电测深曲线的最优化反演方法。采用最优化法进行反演解释，就是要求出与实测电测深曲线呈最佳拟合状态的理论曲线所对应的电性层的层参数，并以其作为实际大地的层参数。在反演时，既可拟合ρs曲线，也可拟合T曲线。图2-70是拟合ρs曲线的程序框图，现将其计算步骤简要说明如下。

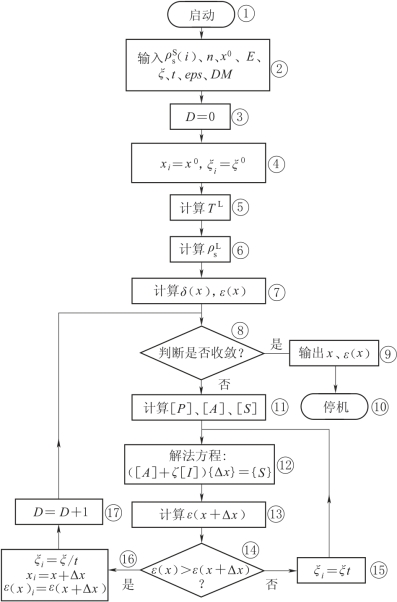
图2-70　拟合ρs曲线的程序框图

步骤①为启动。

步骤③给迭代次数D赋零值，开始进入第一轮计算。

步骤④将电性层参数初始值x0及初始阻尼系数ξ0赋给数组x及阻尼系数ξ。

步骤⑤根据x按递推公式式（2-36）计算理论电阻率转换函数TL。

步骤⑥利用滤波系数E（jΔ）按式（2-46）由TL计算理论视电阻率。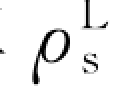

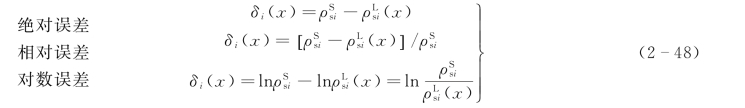
包括m个极距（r1，r2，…，ri，…，rm）的整条实测ρSs曲线与理论ρLs曲线之间的拟合程度，通常以这m个极距上的偏差函数的平方和表示：

式（2-49）中的拟合方差ε（x）称为目标函数，它是层参数的函数。

步骤⑧～步骤⑩根据事先给定的收敛精度要求判定是否收敛。若满足判敛条件，表明已收敛，则转入步骤⑨，打印输出反演结果——层参数x及目标函数ε（x）值，然后停止运算；若未收敛，则转入步骤[11]。

步骤[11]～步骤[12]求层参数的修改量Δx。在反演过程中，如果未收敛，则可以修改层参数，并用修改后的层参数重新计算理论曲线，进行下一次拟合，直到找出两曲线呈最佳拟合时所对应的层参数便是反演解释的结果。这种反演相当于数学上求多变量函数ε（x）的极小值。使目标函数取极小值，即

目标函数又可写为

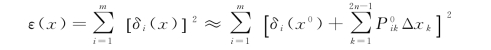
取极值的条件为

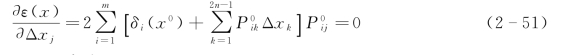
或移项写成

若分别取j=1，2，…，2n-1，可得线性方程组，其矩阵形式为

系数矩阵

[P]为m×（2n-1）阶矩阵，称为雅可比矩阵，其元素为

列矢量{Δx}={Δx1，Δx2，…，Δx2n-1}TΔx

右端项{S}=（S1，S2，…，S2n-1）T=-[P]T{δ0}，其元素为

求解矩阵方程式（2-52）便可求得模型参数修改量Δx。以x=x0+Δx作为新的层参数进行计算。但在这种算法中，层参数初始值选择不当时，迭代可能不收敛。为克服这一缺点，可适当加大矩阵[A]的主对角元素，即把[A]改为[A]+ξ[I]，于是得

式中：ξ=γ2为一适当的正数，称阻尼系数（亦称阻尼因子）；[I]为（2n-1）×（2n-1）阶的单位短阵。

与此对应的目标函数为

步骤[13]重新计算新参数x+Δx所对应的目标函数ε（x+Δx）。

步骤[14]～步骤[15]比较相邻两次拟合的目标函数ε（x）和ε（x+Δx）。若后者大于前者，表明迭代趋向发散，于是转入步骤[15]，将阻尼系数ξ增大t倍后，转向步骤[12]，重新求层参数修改量Δx；如果后者小于前者，说明迭代向收敛方向发展，该次迭代成功，转入步骤[16]。

步骤[16]将阻尼系数减小t倍，以新的模型参数x+Δx代替原参数x，并以新的目标函数ε（x+Δx）代替ε（x）。

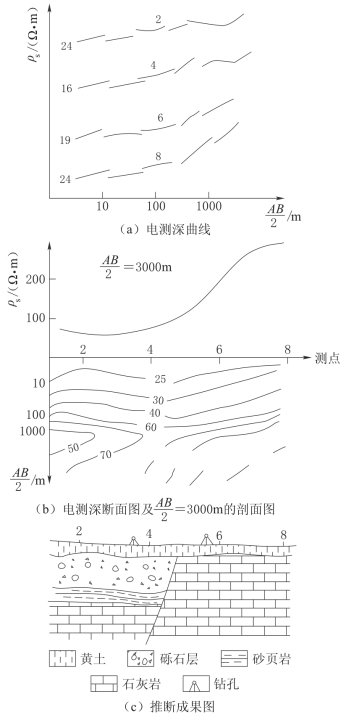
图2-71　通过断层的电测深成果图

步骤[17]将迭代次数D加1后转回步骤⑧，进行下一次迭代计算。