折射波法的资料处理
这里所讨论的折射波法资料处理是对初至折射波而言。首先,必须对地震记录进行波的对比分析,从中识别并提取有效波的初至时间和绘制相应的时距曲线。这一工作可以由人工完成,也可由计算机自动完成。然后根据时距曲线特征,选用相应的方法进行解释工作。
折射波法资料处理系统的一般过程如图7-1中的流程框图所示。从图7-1可以看出,在对地震记录拾取初至时间之前,先判别是否要做预处理。若有的地震记录中初至区干扰波较强,而有效波相对较弱时,则应在预处理中通过滤波、切除或均衡等方法压制干扰波,以保证对有效折射波的识别和正确地拾取初至时间。这一工作对由计算机自动判别拾取初至时更为重要。若地震记录中干扰小,初至折射波很清晰,可直接进行拾取初至时间而不必做预处理。
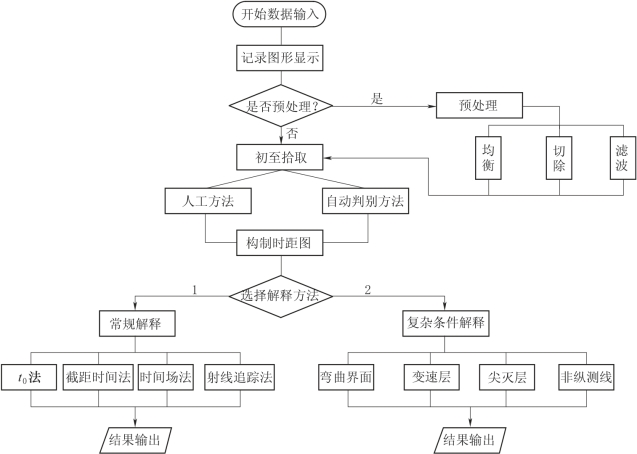
图7-1 折射波法资料处理系统的流程框图
在解释方法选择中,可选常规解释方法和复杂条件解释方法两类。各类中又分别包含有各种不同的方法和不同的情况。通常当折射界面为正常的水平界面或倾斜速度界面时,可选用常规的解释方法;若是其他一些特殊形态的地质体和岩层,则应选用相应的复杂条件解释方法进行解释。
关于各种不同情况的折射波的解释方法,都是根据地震波的射线传播原理和几何关系得出的,由于篇幅有限,这里不可能逐一进行介绍。但为了对折射波解释方法有进一步了解,下面将介绍三种折射波处理解释方法:截距时间法、t0法和时间场法。
1.截距时间法
截距时间法适用于界面为平面的条件,可用它来求界面的深度。对于弯曲的界面,因位于激发点不同侧的时距曲线变得异常复杂,因此必须用其他方法处理。界面以上为多层覆盖层时可用平均速度或交点速度等作为其有效速度V1。
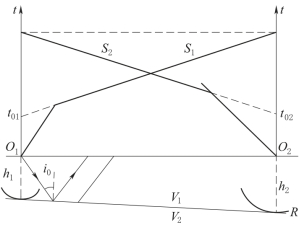
图7-2 截距时间法求界面深度
如图7-2所示,设O1、O2分别为两个激发点,得到两条相遇时距曲线S1和S2。当倾斜界面为平面时,S1和S2都为直线段。将S1和S2延长与时间轴分别交于t01和t02,根据时距曲线方程可写出
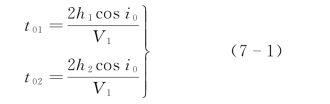
由此,可得震源点O1和O2处折射界面的法向深度h1和h2为
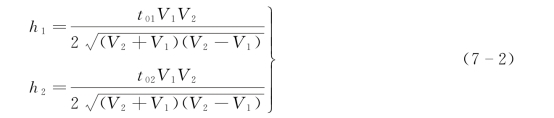
求出h1和h2后,以O1和O2为圆心,分别以h1和h2为半径作圆,然后作这两圆的公切线,便得到所求的折射界面。
2.t0法和差数时距曲线法
此方法是利用t0法绘制折射面,因而用差数时距曲线来求折射界面的速度,该方法的应用前提是:折射界面的曲率半径比其埋藏深度大得多,波沿界面滑行时没有穿透现象。同时要知道波在界面以上介质中的速度。
如图7-3(a)所示,设由炮点O1、O2激震,得到两条相遇折射波时距曲线S1、S2。取测线上任一点S,在相遇时距曲线上分别得到相应的旅行时间t1和t2:

而在O1和O2的互换时间为
![]()
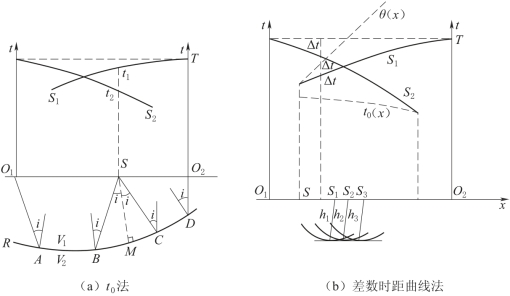
图7-3 t0法和差数时距曲线法示意图
图7-3(a)中,三角形BSC近似于等腰三角形,经过S点作BC的垂直平分线,得到SM=h,于是
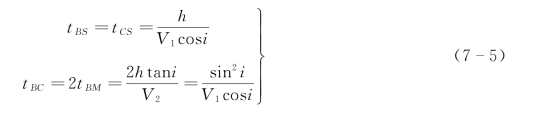
由上述诸式即可求得
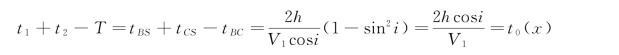 (https://www.daowen.com)
(https://www.daowen.com)
因此,S点到折射界面的法线深度为
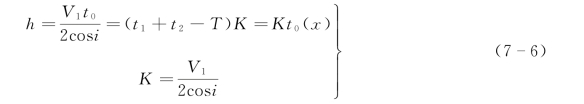
通过测量测线各检波点的t0和K值,就能求得折射界面的法线深度h。求t0(x)的方法是
令
![]()
即先在时距曲线上任一点S处,先量得Δt=T-t2,然后在另一条时距曲线上减去Δt而得到t0,各观测点所得t0均不同,可连成t0(x)曲线,如图7-3(b)所示。
K值求法为
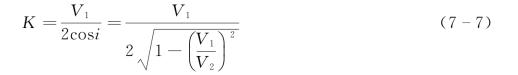
这样,问题就变成求V2值。为求V2值,可引入差数时距曲线:
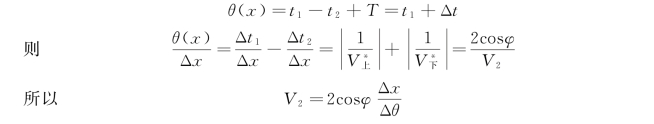
当界面倾角小于15°时,cosφ≈1,则有

上述过程将归纳为以下步骤:
(1)由相遇时距曲线S1和S2作t0(x)曲线和θ(x)曲线。
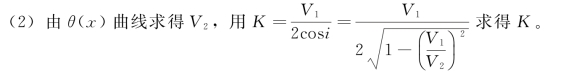
(3)计算每一测点S到折射界面的法线深度h,h=t0(x)K。
(4)以S为圆心,以h为半径作圆弧,对每一检波点均可作出这样的圆弧,这些圆弧的公切线即为折射界面的位置。
3.时间场法(波前法)
时间场法被认为是一种较为精确的绘制折射界面的方法,它适用于均匀介质或不均匀介质,以及规则与不规则的各种界面情况。根据相遇时距曲线和已知界面以上的覆盖层速度V,就可以应用此法较精确地绘制折射界面的形状,而不需要对界面的性质和下伏介质的速度作任何假设。它也能应用在追逐或单支时距曲线条件下,并可以独立给出折射界面上的波传播速度,但要绘制许多等时线,工作量较大。
时间场法是根据实测时距曲线,绘制出波在介质中的时间场,从而进一步勾制出折射界面。如图7-4(a)所示,设折射界面R的上覆岩层是均匀的,波速为V1,S1、S2为两支相遇时距曲线。当在O1点爆炸时,在O2点接收到的时间为tO1ABO2;而在O2点爆炸时,在O1接收到的时间为tO2BAO1。显然,这两个时间应相等(互换时间),即
![]()
在O1和O2爆炸时分别激起的折射波能够在界面上任一点C相遇,且在C点上两个折射波的旅行时之和等于互换时间T,即
![]()

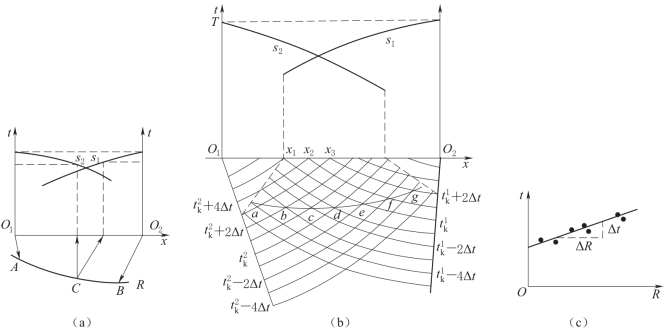
图7-4 用时间场法确定折射界面

