弹性介质中的应力、应变和弹性模量

一、弹性介质中的应力、应变和弹性模量

任何一种固体都介于完全弹性与塑性体之间，但是对大多数物体来说，当外力较小且作用时间很短时，可以把它近似看作完全弹性体。在地震勘探中，大多数介质都能基本上满足完全弹性体这一假设，所以从弹性力学角度出发，可以把地震波看作弹性波而加以研究。

1.应力和应变

2.弹性模量

通常把表征弹性体性质的参数，称为弹性参数，常用的弹性参数如下。

（1）泊松比ν：表示物体受单向拉伸力时，物体的横向应变（横向相对压缩）和纵向应变（纵向相对伸长）之比，表达式为

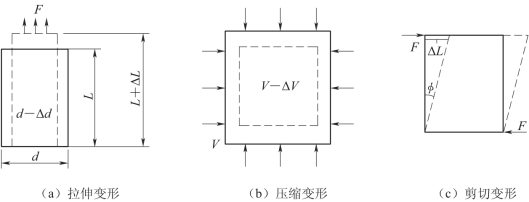
图5-1　应力应变示意图

式中，负号表示横向与纵向应变方向相反。一般岩石的泊松比为0.25。

（2）杨氏模量E：表示物体单向拉伸或压缩时，应力与应变之比，表达式为

杨氏模量可作为物体抵抗应力的量度。

（3）体变模量K：表示物体受各向均匀压缩的情况下，所加压力P与体积相对变化θ之比，表达式为

式中，负号表示随着P值增大，K反而减小。

（4）剪切模量μ：表示物体切应力τ与切应变之比，表达式为

式（5-4）表明，μ越大，切应变越小，μ是阻止切应变的一种量度。对于液体，μ=0，即不产生切应变，因此液体只有体积变化。

（5）拉梅系数λ：表示横向拉应力与纵向应变之比，表达式为

以上五个参量，对于各向同性均匀介质，其中任意一个参量都可用任意两个其他参量表示。例如：

其中λ、μ有时也合称为拉梅系数。