点电流源电场的分布特点
1.一个点电流源的电场
假设在电阻率为ρ的均匀各向同性的地下无限介质中埋有一个供电电极A，由于电极本身的尺寸很小，与电极到观测点的距离相比，小到可以看作一个点，因此称为一个点电流源。另一个供电电极B置于距A很远（可以认为是“无穷远”）的地方，那么A极附近的电场将不受B极的影响，或影响甚微，可以忽略不计。这样就得到一个点电流源的电场[12]。
对于一个点电流源的电场，由于周围介质是均匀的，可以想象，它的场将具有球对称性，故选用球坐标系统，并且把坐标原点置于A极处最为简便。距离A点为r处M点的电位，只和r有关，与球坐标另外两个变量Φ（方位角）、θ（极角）无关。因此，球坐标系统的拉普拉斯方程可简化为
对式（1-21）积分得
对式（1-22）再积分得
c和c1都是积分常数。根据边界条件式（1-14），当r→∞时，U→0，故c1应为零，于是
因为是均匀各向同性介质，所以从A点流出的电流线在各个方向是一样的，呈辐射状。因此，穿过半径为r的球面总的电流强度为I=4πr2J，于是
根据式（1-5）、式（1-10）和式（1-22），得
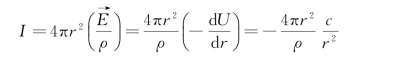
则
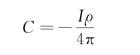
最后得到
式（1-26）是均匀各向同性无限介质中，点电流源电场的电位分布公式。据此，可以写出电阻率和电场强度公式
等电位面是一系列以电极A点为球心，以r为半径的同心球面；电场强度E和电流密度J的方向由矢径确定，呈辐射状。它们的图形是重合的；等电位面处处与E及J正交。
当把供电电极A放在无限大水平地面上向地下供入电流I时（B极为无穷远极），地面上部为空气，电阻率为无穷大。地面以下是电阻率为ρ的均匀介质，这时地下介质就相当于一个均匀各向同性半空间。一个点电流源在均匀各向同性半空间中的电位分布，可以用均匀无限介质中点电流源电场的拉普拉斯方程式求出。另外，在半无限空间介质中，电流只能沿地面以下的半空间分布，其电流密度应比无限空间介质大一倍，则有
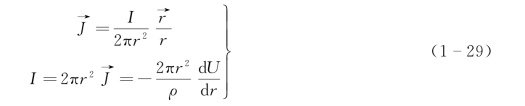
由式（1-22）得
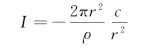
故
因此M点的电位、电阻率、电场强度分别为
电流线以点电流源A为中心向周围呈辐射状分布，如图1-2所示。等电位面为一系列以A点为中心的同心半球面，J的方向与矢径r的方向一致，处处与等电位面正交。电位、电流密度和电场强度均与供电电流强度成正比，而电位与r成反比，电流密度和电场强度与r的平方成反比。
2.地表两个异性点电流源的电场
在地下为均匀介质的地面上，放置两个极性相反的电极，电流+I由A极输入地下，而由B极（-I）自地下流出，构成闭合回路。当两电极彼此相距不远时，根据电场的叠加原理，地下半空间某点M的电位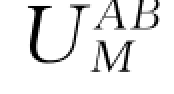
应是A、B两电流源分别在该点产生的电位
、
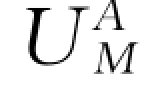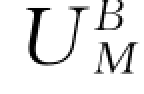之和。
根据式（1-30）得
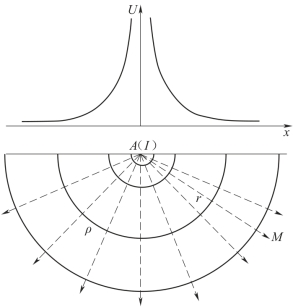
图1-2 地面上一个点电流源的电场
（图中下半部分的实线为等电位线，虚线为电流线）
式中：AM、BM为A点或B点与M点间的距离。
在M点的总电位为
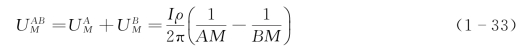
同理，可求出两个异性点电源在M点的电场强度：
由式（1-33）及式（1-34）计算的两个点电流源的电位及电场强度的变化曲线如图1-3（a）所示。它表明在地面A、B连线AB上，靠近电极处电位变化快，即在A极附近电位迅速增高，在B极附近电位迅速降低，而在AB中间1/2～1/3的地段电位变化较慢，其中点电位为零。由于电场强度等于电位的负梯度，故在电极附近电位曲线变化大的地方，电场强度的绝对值也大。在AB中间1/2～1/3的地段内，电位变化不大，电场强度值也变化不大，接近于常数。电流线基本与地面平行，呈现均匀场的特点。
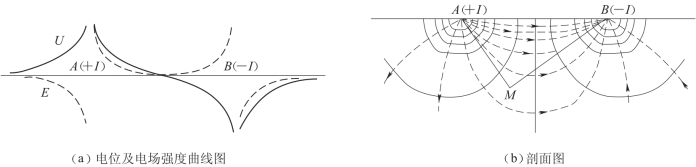
图1-3 两个异性点电流源的电场
（等电位面为实线，电流线为虚线）
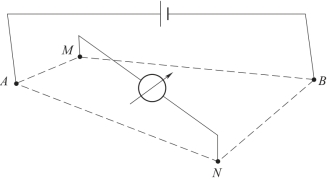
图1-4 任意四极装置示意图
如图1-3所示，前面已计算了A极、B极在观测点M上产生的电位UAMB。同理，很容易求出地面电阻率法中A极、B极在另一观测点N上的电位（图1-4）为
于是A极、B极在M、N两点间产生的电位差为
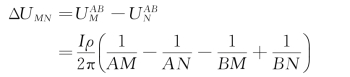
从而得到电阻率公式：
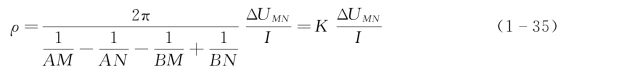
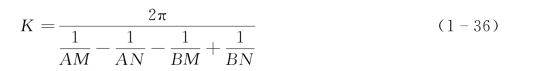
式（1-35）和式（1-36）是在地面上或在岩石露头上测定均匀各向同性半无限介质真电阻率的公式。K为装置系数或排列系数，决定于各电极间的相对位置。