流量测井曲线的解释
在采集和解释流量测井资料之前,需要用流量计进行刻度,以确定涡轮转速N与流量Q的对应关系。有两种刻度方法:一种是室内模拟井刻度方法,是在室内预先设计好的模拟井中进行的,刻度时把流量计放入井内,按照实际操作过程即可作出每支仪器的标定曲线,利用这种曲线作为图版即可将实测数据转换成流量;另一种是现场刻度方法,是在现场实际井中进行的,主要用于对连续流量计的刻度。
(一)确定含水层的层位以及各含水层之间的水力联系
利用流量曲线分析井内水流状态不仅可以确定出水层或吸水层的层位,而且还可了解各层之间的水力联系,综合评价坝基渗漏等问题。
当钻孔穿过多个含水层时,井内水流将从水头较高的层位流向较低层位,而当向井内注水或抽水时,则根据混合水位与各层静止水位的关系而使水流发生变化,这种变化包括水流方向的改变,以及原来渗出的变为渗入或原来渗入的变为渗出。
图10-69为某一井段的实测流量曲线。由图10-69可见,该井段有三个含水层段,最下一层为出水层,且水量较大,上面两层为吸水层,其特征为随水流方向(由下向上)流速逐渐减小,根据流量曲线特征可以判断由M1层流出的水一部分流入M2、M3层,还有一部分流向地面或其他地层。如果流量计已被刻度,则根据流量曲线可直接读出各层的涌水量和吸水量:
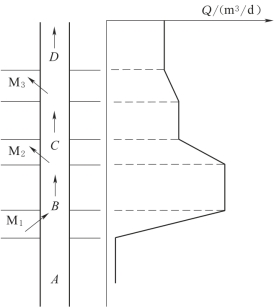
图10-69 实测封隔器流量计的流量曲线
M1层的涌水量
![]()
M2层的涌水量
![]()
M3层的涌水量
![]()
总出水量
![]()
QA、QB、QC、QD为各个相应隔水层段的流量值,如果D以上没有其他含水层或漏水层,则所计算的q值为该井的地面产水量qsc。如果两者不一样,则就说明在D以上井段有漏水或渗水部位。各含水层的顶、底板可由流量曲线倾斜增大或下降的突变点来确定。
 (https://www.daowen.com)
(https://www.daowen.com)
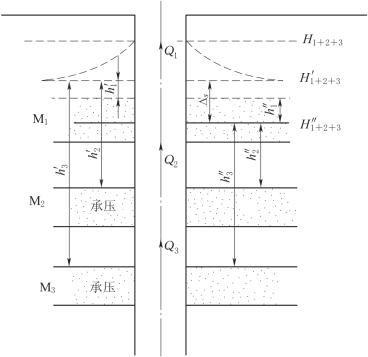
图10-70 两次混合抽水计算渗透系数示意图
(二)求解含水层的渗透系数
长期以来主要依靠水文地质抽水试验来求渗透系数,这一方法要求事先确定含水层位厚度、抽水时水位降深以及相应的流量等一系列数据。如果钻孔揭露多个含水层则还需要分层止水、分层抽水才能求解。显然,这很费时、费力,而且往往由于分层止水不够准确而导致求解结果误差很大。采用流量测井可以避免这些缺点,而且效果更好。
利用流量测井确定渗透系数仍然以Dupuit公式为依据,但需要通过二次混合抽水(或注水)、二次降深过程。当条件有利时(如天然涌水量较大的含水层)也可只一次降深就解出。
以实例说明具体方法。在图10-70中有三个含水层,最上的M1层为潜水层,M2、M3为承压含水层,设各层的渗透系数和静止水位分别为K1、K2、K3和H1、H2、H3。H1+2+3为井内混合静水位。当某一含水层的静止水位高于混合水位时为排水,低于时为吸水,等于时则不排水也不吸水。根据这一原理,通过抽水降低混合水位,使H1+2+3降到H'1+2+3,促使各个含水层向井内涌水。此时用流量计测得一条流量曲线,并由此可确定各含水层的层位及厚度,以及各个含水层的涌水量或吸水量Q'1、Q'2、Q'3,若含水层涌水时Q值取正,吸水时Q值取负,根据Dupuit公式,可得如下方程:
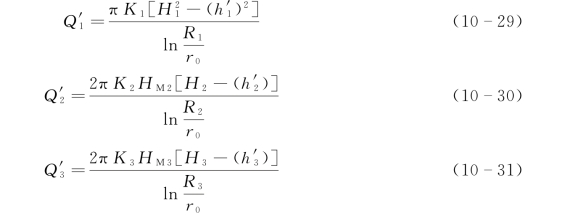
式中:h'1、h'2和h'3分别为M1、M2和M3含水层的顶板到第一次抽水后的混合水位H'1+2+3的距离;H1、H2和H3分别为M1、M2和M3各含水层的静水位(水头);HM1、HM2和HM3分别为各相应含水层的厚度;K1、K2和K3分别为M1、M2和M3含水层的渗透系数;R1、R2和R3为各含水层抽水时的影响半径;r0为井的半径。
当测完第一条流量曲线后,再增大抽水量使混合水位由H'1+2+3降到H″1+2+3,然后再做第二次流量测井,同理可以得到各个含水层的涌水量或吸水量Q″1、Q″2和Q″3,使用M1、M2、M3含水层的顶板到第一次第二次抽水后的混合水位H″1+2+3的距离h″1、h″2、h″3。
这里,假设第一次抽水和第二次抽水时的影响半径R不变,这在抽水量不太大的情况下是与实际情况相符的。这样,对以上两个方程组分别求解,即可得
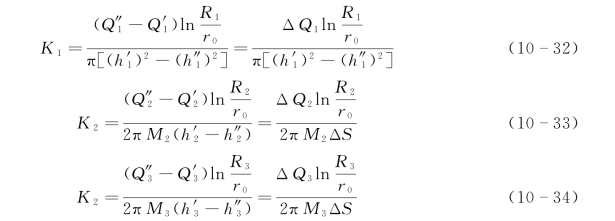
在式(10-32)~式(10-34)中,Q'1、Q'2、Q'3、Q″1,Q″2,Q″3分别由流量测井曲线读出,ΔS为两次混合抽水的水位差,可以直接测出,r0可由井径曲线读出,R1、R2、R3可由水文地质资料取得,由于R包含在ln函数之内,因此数值大小对K值计算影响不十分敏感,一般对各个含水层不必分别求取。
如果含水层的自然涌水量较大,也可只用一次混合抽水过程求得渗透系数,此时应先测一条自然流量曲线(设相应的混合水位为a),然后抽水将水位降至b,再测一条流量曲线,利用式(10-32)~式(10-34)也可解得各层的渗透系数k值。
(三)确定含水层的静止水位
利用式(10-29)~式(10-34),用反推的方法可以解得各含水层的静水位表达式为
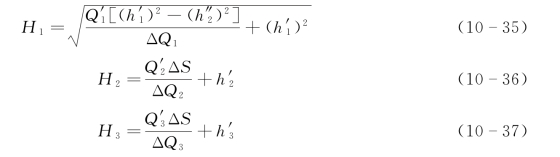
也可用作图方法求解各层的静止水位,其具体方法是根据多次抽水的水位S以及相应的流量测井值Q作出Q-S散点分布图,并进而作Q=f(S)回归曲线,根据回归曲线的顺延线与Q轴的交点即可确定相应的静止水位H值。根据所求回归方程可以预测在一定降深条件下的各层涌水量。
