一、数字滤波
在资料解释中,需要识别和追踪有效波,面干扰波和有效波混在一起,给解释工作增加了困难。因此,需要寻找一种过滤或筛选的办法,把有效波从各种干扰波中分离出来。所以对地震波提出了进行过滤的问题,即所谓滤波。滤波的目的就是提髙信噪比,把干扰波滤掉或削弱,保留或相对增强有效波。
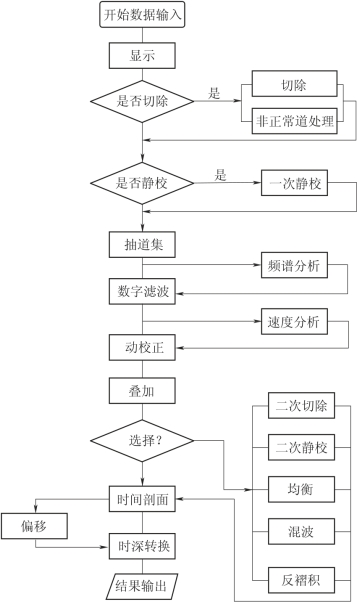
图7-5 浅层反射法资料处理系统一般流程框图
数字滤波种类很多,从性质上可分为线性滤波和非线性滤波两大类。本节介绍的一维频率滤波和二维数字频率波数滤波都属于线性滤波,它们是地震数字处理中常用的基本方法,是常规处理中的基本内容。
(一)一维频率滤波
所谓一维频率滤波是利用有效波与干扰波在频率成分上的差异,设计出一个滤波器,通过对数字信号进行特定的运算而完成。由于用时间函数x(t)或对应的频谱X(f)表示地震道都是等价的,故数字频率滤波可以在频率域或时间域进行。下面分别介绍频率域滤波和时间域滤波。
1.频率域滤波
进行滤波的目的是要削弱干扰波,突出有效波。因此,首先要了解有效波和干扰波在频谱上有何差异,然后才设计出滤波器的频率响应,以进行滤波。
设地震道x(t)的频谱为X(f),其中有效波的频谱为S(f),干扰波的频谱为N(f),而且S(f)≠0时N(f)=0,见图7-6(a)。设滤波器的频率响应函数为H(f)[图7-6(b)],且满足:
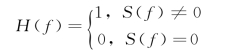
当进行滤波处理时,则用H(f)与x(t)的频谱X(f)=S(f)+N(f)相乘,得
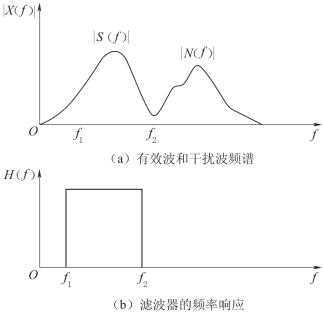
图7-6 地震道的频谱及滤波器的频率响应
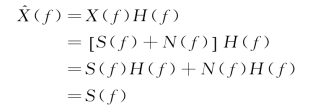
![]()
通过上述运算消去了干扰波,保留了有效波。上面地震波的频谱是较典型的。一般干扰波的频谱N(f)与有效波S(f)并不完全分离,但可以近似地看作分离,只要设计出合适的频率响应函数H(f),通过滤波也可以达到提高信噪比的目的。
由上述运算知频率域滤波方程为
![]()


由式(7-9)~式(7-12)得

式(7-9)表明:频率域滤波在数学上是通过将x(t)的频谱X(f)与滤波器的频率响应H(f)相乘而实现的。

频率域滤波方程建立完成,下面介绍滤波的主要步骤。设已知一个地震道x(t),它包含有效波s(t)和干扰波n(t),见图7-7。现需对x(t)进行滤波处理。
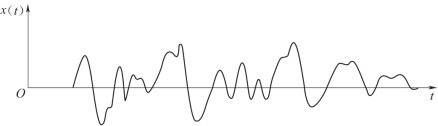
图7-7 滤波前地震记录
(1)对地震记录x(t)进行频谱分析。通过频谱分析结果,了解到有效波s(t)的主要频率成分在f1~f2范围内,干扰波主要频率成分在f3~f4范围内,二者基本上是分开的,见图7-8(a)。
(2)设计合适的滤波器。为了滤去干扰波的频率成分,针对频谱分析结果,设计一个带通滤波器,其频率响应为:
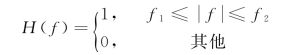
其图形见7-8(b),该滤波器能把干扰波滤掉,保留有效波。
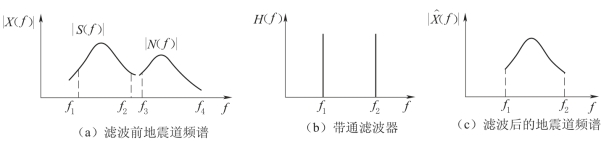
图7-8 滤波前后地震道频谱
(3)进行滤波运算。根据频率域滤波方程式(7-9),令x(t)的频谱X(f)与滤波器的频率响应H(f)相乘,得
![]()

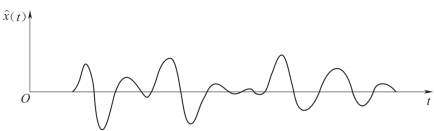
图7-9 滤波后的地震记录
频率域滤波的整个运算过程见图7-10。

图7-10 频率域滤波运算框图
从频率域滤波过程来看,对地震道x(t)进行滤波,要进行一次傅里叶正变换和一次反变换。以往由于在计算机进行傅里叶运算要花费很多时间,因此这种方法很少应用。近年来,由于采用了快速傅里叶变换算法,缩短了运算时时,这种方法才得到较广泛的应用。
2.时间域滤波
根据上面建立的频率滤波的方程,以及信号和滤波器的特性在频率域表示与时间域表示可以互换的关系,可以很容易地建立时间域滤波方程。
设滤波器的频率响应为H(f),其对应的脉冲响应为h(t);输入地震道为x(t),其相应的频谱为X(f),输出地震道为x^(t),其对应的频谱为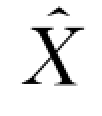 (f)。
(f)。
从式(7-9)知,频率域滤波方程为(https://www.daowen.com)
![]()
根据频谱褶积定理可得
![]()
*表示褶积运算,式(7-15)即为时间域的滤波方程。由于频率滤波在时间域是一种褶积运算,故把在时间域的滤波又称为褶积滤波。
式(7-15)运算的连续形式为
![]()
其离散的形式为
![]()
式中:Δ为采样间隔;x(nΔ)为输入离散的地震道;x^(nΔ)为输出离散的地震道;h(mΔ)为离散的脉冲响应。
式(7-17)中求和号前面的Δ是一个常数。我们可以省略去,略去后滤波结果相差一个常系数,对滤波后信号频谱的相对关系无影响。为了方便,可以把式(7-17)简化为
![]()
在实际运算中,m的取值范围都不可能是(-∞,+∞),而只能取有限长度,即[-M,M]。这样,又会给滤波效果带来影响。
(二)二维数字频率波数滤波
从上述一维频率滤波知道,频率滤波的前提条件是地震信号的有效波和干扰波具有明显的差异,否则,是难以把有效波分离出来的。但是当这种前提条件不存在时,我们可以利用不同时间、不同距离的多道地震记录x(t,l)上接收的有效波与干扰波在频率-波数谱上的差异进行二维数字频率波数滤波(以下简称二维滤波)。
二维滤波可以在频率一波数域进行,也可以在时间一空间域进行,因此,二维滤波要涉及两个自变量(t,l)或(f,K),表示波数。它的数学基础是二维傅里叶变换和二维褶积运算。

1.在频率-波数域的二维滤波
设地震记录为x(t,l),则
![]()
式中:s(t,l)为有效波,对应的频波谱为S(f,K);n(t,l)为干扰波,其频波谱为N(f,K)。
x(t,l)的频波谱为
![]()
希望二维滤波后的输出为
![]()
要实现滤波目的,显然要求(图7-11):
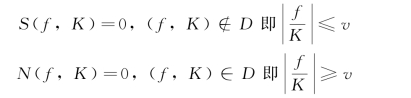
式中:D为f-K平面中一个区域,符号“∈”表示属于,“∉”表示不属于。
根据f-K平面上有效波和干扰波的分布特点,可以设计出需要的二维滤波器的频波响应为

将H(f,K)与X(f,K)相乘可得二维滤波的输出:
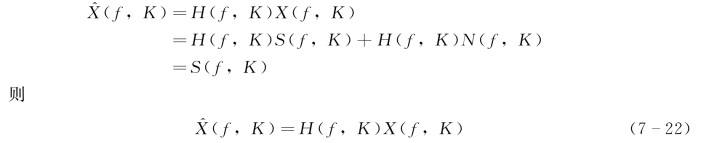
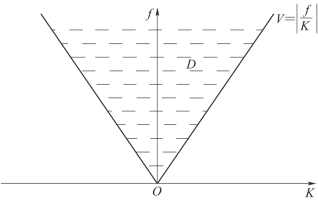
图7-11 f-K平面分析

从上述的讨论可见,要进行二维滤波,必须要找出有效波和干扰波在频波谱上的差异。这是二维滤波的前提,有此前提条件,才能保证二维滤波的效果。
2.时间-空间域的二维滤波
设二维滤波器的频率-波数响应为H(f,K),其滤波因子为h(t,l),通过反变换求得滤波因子
![]()
若输入为x(t,l),对应的输出为x^(t,l),类似于一维滤波,在时间-空间域的二维滤波方程为
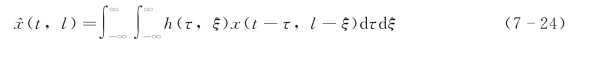
其滤波过程如图7-12所示。在实际运算时,需把式(7-23)改写成离散化的二维数字滤波公式:
![]()
式中:n、p分别为地震波和滤波因子的时间采样序号;m、q分别为地震波和滤波因子的空间采样序号;Δ为时间采样间隔;∇为空间采样间隔。
![]()
图7-12 二维滤波
