三、频谱分析
频谱（振幅谱）表示波的能量相对频率的变化规律。频谱分析就是利用傅里叶分析从地震信号x（t）中求取其频谱X（f）的过程。频谱X（f）则反映出组成地震信号的各谐振分量的振幅、初相与其频率的关系。频谱分析的目的在于了解有效波和干扰波的频谱分布范围，以便选取合适的频率滤波器，压制干扰波，突出有效波，提高记录的信噪比，此外还为进行岩性岩相解释等提供参数。
根据离散傅里叶变换理论可知，若给出时间序列x（nΔ），其中Δ为时间采样间隔，n=0，1，…，N-1，N（N为采样点数），x（nΔ）的频谱为X（md），则有
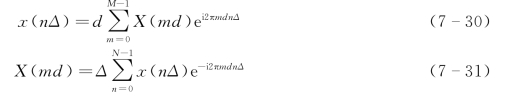
式（7-30）和式（7-31）组成了离散傅里叶变换对。从式（7-31）可知，X（md）的实部ReX（md）和虚部ImX（md）分别为
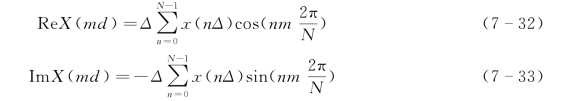
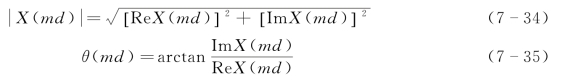
频谱分析时要考虑如何选择参数Δ和N，它们影响着频谱分析的精度。
1.采样间隔Δ的选取原则
根据采样定理，要求采样间隔Δ满足：
式中：fc为地震信号x（t）的截止频率，即x（t）最高可能达到的频率，如果Δ=4ms，那么，截止频率为125Hz。
2.参数N的选取原则
连续的地震信号x（t）经过采样后，截取出其中某一段离散的地震信号x（nΔ）（0＜n＜N-1）来做频谱分析，从有限傅里叶分析知，有限离散频谱的频率间隔为
因此，要求N满足：
式中：fδ为地震信号的频率分辨间隔。
为进行频谱分析的最小记录长度。
选取N时要求满足式（7-37），即要求记录长度NΔ不小于最小记录长度。又因为一般频谱分析程序都采用快速傅里叶变换算法，因此，一般还要求N=2k，k为正整数。
为减小选取时窗端点截断因素影响，在频谱分析时，应在时窗两侧取一斜坡值或镶边。当地震资料反映的薄层较多、层间距较小时，为了对某一波组进行频谱分析，斜坡值应取小些，否则，将不可避免地把相邻层的振动取入分析时窗，以致歪曲有分析价值的细节。对二维信号f（t，x）的频谱分析，我们采用二维傅氏变换计算，其结果为f-k谱。