地震波传播的基本原理
1.惠更斯-菲涅尔原理(波前原理)
假设地质体为均匀介质,地面O点为震源。当O点振动后,地震波就从这一时刻起自O点向各个方向传播。如果把某一时刻介质中所有刚刚开始振动的点连成曲面,该曲面称作此时刻的波前。如果把同一时刻所有刚停止振动的点连成曲面,则此曲面称波后(波尾)。
如图5-6所示,在波前以外的质点,因波动尚未到达,故没有振动,而波后以内的质点已停止了振动。在波前和波后之间的介质质点处于振动状态,这个区间称为振动带。
惠更斯-菲涅尔原理就是说明波前向前传播规律的原理。该原理表明:在弹性介质中,任何时刻波前的每一质点,都可以看作一个新的点震源,由它产生的二次扰动形成子波前,而以后新的波前位置可以认为是该时刻各子波波前的包络面。
该原理也称为波前原理。根据这个原理,可以用作图法求任一时刻的波前。如果某时刻的波前为一球面S0,可以在S0上找若干个点,以这些点为中心,以r=VΔt为半径作圆弧(V为波的传播速度),再作圆弧的包络面,即可得到t+Δt时刻的波前S。在各向同性均匀介质中,波前是以震源为中心的一系列球面。当半径很大时,在球面波上很小的一部分就可以看作为平面波,如图5-7所示。
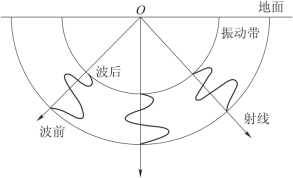
图5-6 地震波传播示意图
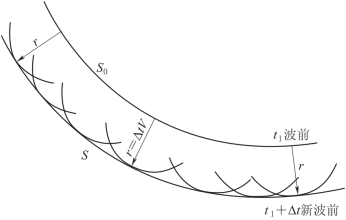
图5-7 波前原理示意图
2.费马原理(射线原理)(https://www.daowen.com)
所谓射线,就是波从一点到另一点传播的路径。弹性波沿射线传播的旅行时间与沿任何其他路径传播时间相比是最小的,这就是费马的最小时间原理(也称为射线原理)。在均匀各向同性完全弹性的介质中,射线为自震源发出的一簇辐射状直线,射线垂直于波前。
用射线和波前来研究波的传播,是一种用几何作图来反映物理过程的简单方法,也叫几何地震学,它只能说明波传播中不同时刻的路径和空间几何位置,但不能分析能量的分布问题。
3.互换原理
在介质中的A点施加力F(t),该力引起另外一点B的瞬时位移为D(t)。反之,如果在B点施加一外力F(t),则在A点也会引起同样的瞬时位移D(t)(图5-8)。所谓互换原理,就是指震源和观测点(检波器所在点)的位置可以互换,在此情况下,同一波的射线路径保持不变。
互换原理普遍适用于任意形状界面的弹性介质、非均匀介质和各向同性介质。地震勘探中的相遇时距曲线的观测系统就是以该原理为基础的。
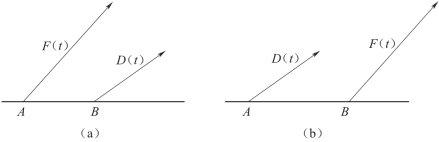
图5-8 互换原理示意图
4.叠加原理
若有几个波源产生的波在同一介质中传播,且在空间某点相遇,则相遇处质点的振动是各个波所引起的分振动的合成。介质中某质点在任一时刻的位移便是各个波在该点所引起的分矢量之和。换言之,每个波在空间的传播是独立的,几个波相加的结果等于各个波作用之和,这种性质称之为叠加原理。
