资料处理及解释

四、资料处理及解释

常时微动的资料处理方法主要有两种，一种是周期频度分析法，另一种是频谱分析法。目前常时微动观测资料处理普遍采用频谱分析法。

周期频度分析法是通过计算各种周期成分的波所出现的次数，从而得出波形和周期特性。具体做法是在观测记录中选取质量较好的记录段，按波形正反向变化大致对称划一条零线，波形与零线形成一系列的交点，取相邻两点时差的二倍作为相应波的周期。依次读取并进行统计，以周期为横坐标，以不同周期波形出现的次数为纵坐标，即得到各种周期的频度曲线。频度最高的周期称作优势周期，记录中周期最大的称作最大周期，用出现于记录波形上的波数除记录长度（时间）所求出的周期称作平均周期。该方法早期多以手工进行，后来用频度分析仪进行，其分析结果可近似代替频谱分析，还可消除一些高频干扰。对于周期小于1s的常时微动，两种方法的处理结果在实际应用中效果相同，见图8-42。

设常时微动为时间的函数，用x（t）表示，则将它变换到频率域的傅氏积分为

此外，利用X（ω）及其共轭复数X*（ω）还可以求得功率谱P（ω），即

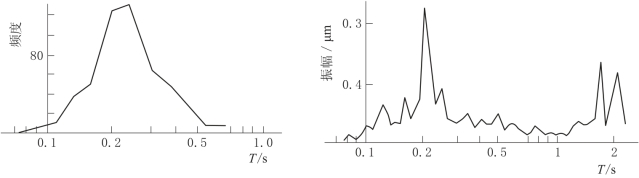
图8-42　微动的频度曲线与傅氏谱比较

在实际解释中，将明显混入噪音的时间段剔除不用，用各时间段波形功率谱的算术均值即可求得平均功率谱，即

一般取10s为一个时间段，这样大约做20次左右的叠加，就能得到其观测点的比较稳定的功率谱。功率谱与傅氏谱并无本质区别，二者大体上存在平方关系，可理解为功率谱强调结构物对某些频率成分的波的影响。如果对功率谱进行傅氏变换，就可得到自相关函数：

自相关函数是表示将波形函错位移动时间t时与原波形相关程度。该值越大，则表示相关程度越好，且相关相邻峰值的时间差，即为该波形的卓越周期。