三、基本原理
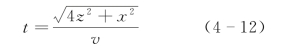
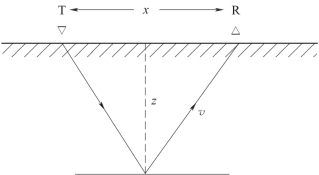
图4-9 雷达反射原理图
当地下介质中的波速v（m/ns）为已知时，可根据精确测得的走时t（单位为ns，1ns=10-9s），由上式求出反射物的深度（m）。
波的双程走时由反射脉冲相对于发射脉冲的延时进行测定。反射脉冲波形由重复间隔发射（重复率20～100k Hz）的电路，按采样定律等间隔地采集叠加后获得。考虑到高频波的随机干扰性质，由地下返回的反射脉冲系列均经过多次叠加（叠加次数从几十至数千）。这样，若地面的发射和接收天线沿探测线以等间隔移动时，即可在纵坐标为双程走时t（ns）、横坐标为距离x（m）的探地雷达屏幕上绘描出仅仅由反射体的深度所决定的时-距波形道的轨迹图（图4-10）。与此同时，探地雷达仪即以数字形式记下每一道波形的数据，它们经过数字处理之后，即由仪器绘描成图或打印输出。
反射脉冲波形明显程度，是探地雷达图像地质解释的重要依据。它决定于发射脉冲波的能量、波在地质界面上的反射特性以及波在地下介质中行进时的衰减条件。发射脉冲的幅度，一般为100～200V或更大范围，它是受高频窄脉冲电路的限制的。反射特性则决定于物性界面的波阻抗差别，并以反射系数作描述。对于平面波，反射系数为
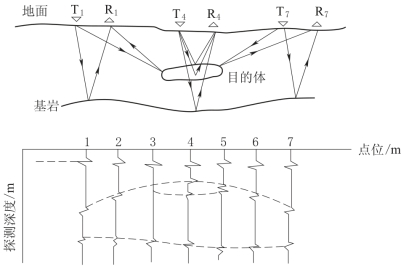
图4-10 雷达剖面记录示意图
Z为法向波阻抗，由介质的复介电常数、磁导率和入射角（不同极化波具有不同的三角函数形式）决定。下角标指示出波所在介质。可以看出，由于介质具有导电性，反射系数呈复数形式。对于非平面波，此值将在几何光学条件下仍起主导作用。若考虑位移电流为主，则
εr为相对介电常数。这样，对于土壤与花岗岩的交界面，反射系数模值R≈0.3333（二者的εr分别设为20和5），即反射能量为入射的33.33%。湿灰岩与湿花岗岩（εr各为8，7）接触，则为0.0334，即3.34%。可见介电常数对反射系数的影响十分重要，而含水性则与εr值密切相关。
波在有耗介质中的衰减是由于传导电流的热损耗和介质极化过程中的附加损耗。除了这些本质原因外，还有波的空间发散损耗和散射损耗。若仅考虑前一原因，以吸收系数α表征的波衰减特性与介质性质的理论关系为
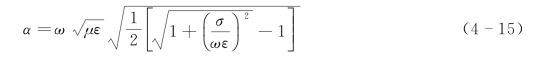
式中：μ、ε和σ分别为介质的磁导率、介电常数和电导率，σ单位为S/m；ω=2πf，为角频率。
对于低导介质：
α正比于σ，且与εr呈根号反比关系，单位为Np/m。在一般介质中，α还与f有关，大致是随f升高而加大。
波速（相速）的确定，使探地雷达的双程时间可转换为深度。速度为
式中：λ为波长。
而角波数k的虚部
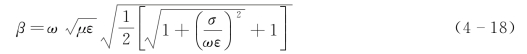
称为相位系数。对于低导介质：
于是
f＇为以MHz计的频率，v为以m/ns计的速度。这样，空气、水和灰岩（εr分别为1、81、9）三种介质中，对应于100MHz频率，波长分别为3m、0.33m和1m，而v则分别为0.3m/ns、0.033m/ns和0.1m/ns。
以上表明，角波数（波传播常数）k（=α+iβ）在探地雷达波传播中具有十分重要的作用。
可以用雷达方程来综述波信号在地下介质中的传递过程（图4-11）：
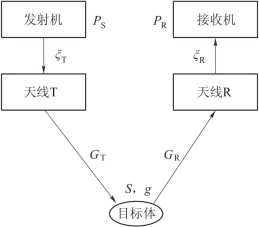
图4-11 波信号在地下介质中的传递过程
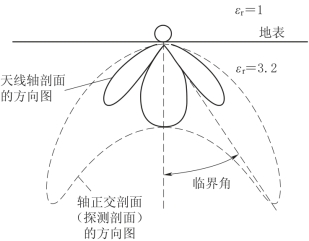
图4-12 天线具有设计的方向性
dF（=2rF）为菲涅尔主值带直径，Z为深度。如果有限目标体的有效反射面直径大于此值，则可以按几何光学的反射方法加以处理，并认为探测是有效的。
综上所述，天线是探地雷达的重要部件，它直接影响着探测质量。探地雷达天线一般采用分离形式，以便于适应现场的不同工作方式。理论上，作为发射或接收天线，两天线的结构和性能是相同的。作为传感器，它的性能主要反映在能量空间分布特性、发射和接收效率问题和电路特性等方面。天线的传播空间方向性图是表征发射（或接收）能量空间分布的一种特性图。图4-12说明了在电偶极天线紧密结合于空气大地交面上时方向指向地下及空中后方的轴线在垂直方向剖面（即测线剖面）上的能量分布。电导率和介电常数比空气大的地下介质的电参数，使电磁波地下能量呈集中向下分布的形态。其最大能量出现在天线轴线两边的临界角方向上（最大能量等于sin-1n，n为折射率；在位移电流为主的介质中等于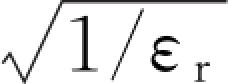
），而后向发射却呈极微弱的球状分布。显然，这种天线具有较优良的辐射性能。在与地面耦合较佳条件下，可以获得较高的辐射效率，甚至毋需向后屏蔽。天线的辐射功率是低于输入功率的，理论上，天线应在谐振条件下工作，这就要求严密设计天线电路和考虑地下介质的耦合问题。电路设计还要充分考虑发射波形的探测特点，即宽带、窄波、高峰值、少余振等要求，使子波呈陡沿、高分辨和单峰，使记录图像清晰。
探地雷达图像由于呈时-距关系形式，因此，类似于地震记录剖面，画面的直观性较强，波形图面上同一反射脉冲起跳点所构成的同相轴可用来勾画出反射界面。当然，对于有限几何体的界面，只要返回的能量足够，图面的各道记录上均可追踪反射脉冲同相轴，这自然就歪曲了目的体的实际几何形态。一般而言，在有限体的边、角部位，常因绕射现象而使图像复杂化。例如，点状体的异常呈双曲线的一叶形态，其峰顶的横向和纵向位置即为点体的地面位置和深度。介质速度越小，异常峰尖就越明显；埋深越大、天线距越大，双曲线就越平坦。类似于地震剖面，为达到直观效果，必须对图像进行偏移归位校正。