2.1.1 条分法
条分法是在1916年由瑞典人彼德森提出的，以后经过费伦纽斯、泰勒等人的不断改进。他们假定土玻稳定问题是个平面应变问题，滑裂面是个圆柱面，计算中不考虑土条之间的作用力，土坡稳定的安全系数是用滑裂面上全部抗滑力矩与滑动力矩之比来定义的。20世纪40年代以后，随着土力学学科的不断发展，也有不少学者致力于条分法的改进，他们的努力大致有两个方面：其一是着重探索最危险滑弧位置的规律，制作数表、曲线，以减少计算工作量；其二是对基本假定做些修改和补充，提出新的计算方法，使之更加符合实际情况。其中毕肖普等提出的关于安全系数定义的改变，对条分法的发展起了非常重要的作用。和一般建筑材料的强度安全系数相似，毕肖普等将土坡稳定安全系数FS定义为沿整个滑裂面的抗剪强度V与实际产生的剪应力τ之比，即
这不仅使安全系数的物理意义更加明确，而且使用范围更广泛，为以后非圆弧滑动分析及土条分界面上条间力的各种考虑方式提供了有利条件。
在滑动土体n个土条中任取一条记为i，如图2.1所示，其上作用的已知力有：土条本身重量wi水平作用力（例力地震惯性力）Qi，作用于土条两侧的孔隙压力（水压力）Ui及Ur，以及作用于土条底部的孔隙压力Ui。另外，当滑裂面形状确定以后，土条的有关几何尺寸如底部坡角αi，底长li以及滑裂面上的强度指标c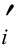
、tgφ
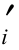也都是定值。因此，对整个滑动土体来说，为了达到力的平衡，我们所要求的未知量如下。
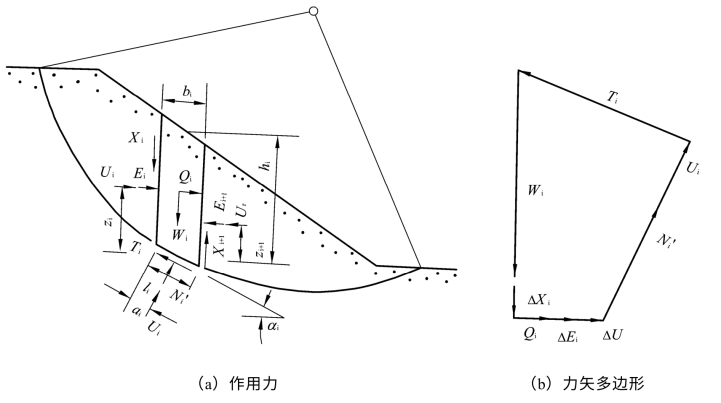
图2.1
（1）每一条土条底的有效向反力N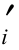
，计n个。
（2）安全系数FS（按安全系数的定义，每一土条底部的切向力Ti可用法向力Ni及FS求出），1个。
（3）两相邻土条分界面上的法向条间力Ei，计n-1个。
（4）两相邻土条分界面上的切向条间力Xi，（或Xi与Ei的交角θi），计n-1个。
（5）每一土条底部Ti及Ni合力作用点位置αi，计n个。
（6）两相邻土条条间力Xi及Ei合力作用点位置Zi，计n-1个。
这样，共计有5n-2个未知量，而我们所能得到的只有各土条水平向及垂直向力的平衡以及力矩平衡共3n个方程。因此，土坡的稳定分析问题实际上是一个高次超静定问题。如果把土条取的极薄，土条底部Ti及Ni合力作用点可近似认为作用于土条底部的中点，αi为已知。这样未知量减少为4n-2个，与方程数相比，还有n-2个未知量无法求出，要使问题得解就必须建立新的条件方程。这有两个可能的途径：一种是引进土体本身的应力—应变关系，但这会使问题变得非常复杂；另一种就是作出各种简化假定以减少未知量或增加方程数。这样的假定大致春下列三种：
（1）假定n-1个Xi值。其中最简单的就是毕肖普在他的简化方法中假定所有的Xi均为零。
（2）假定Xi与Ei的交角或条间力合力的方向（这个方向通常通过试算加以确定）。属于这一类的有斯宾塞法、摩根斯坦—普赖斯法、沙尔玛法似及目前国内工业、民用建筑及铁道有关部门使用很广泛的不平衡推力传递法等。
（3）假定条间力合力的作用点位置。例如简布提出的普遍条分法。作了这些假定之后，超静定问题就可以转化为静定问题，而且，一般来说，这些方法都并不一定要求滑裂面是个圆柱面。但各类方法的计算步骤大都仍然非常复杂；一般均需试算或迭代，好在电子计算技术发展很快，那些烦琐的计算步骤均可编成固定的程序，在电算机上只要花费几分钟时间，就可对最复杂的问题得出完满的结果。
考虑土条条间力的作用，可以使稳定安全系数得到提高，但任何合理的假定求出的条间力必须满足下列两个条件：
（1）在土条分界面上不违反土体破坏准则。亦即由切向条间力得出的平均剪应力应小于分界面土体的平均抗剪强度，或每一土条分界面上的抗剪安全系数Fu必须大于1（作为平衡设计，Fu应不小于FS）。
（2）一般地说，不允许土条之间出现拉力。
如果这些条件不能满足，就必须修改原来的假定，或采用别的计算方法。为此，对于考虑条间力作用的各种方法，稳定分析的最后结果，除求出滑裂面上的最小安全系数Fsmin以外，还要求出各土条分界面上的安全系数Fu以及条间力合力作用点的位置以资校核。
研究表明，为减少未知量所做的各种假定，在满足合理性要求的条件下，其求出的安全系数差别都不大。因此，从工程实用观点看，在计算方法中无论采用何种假定，并不影响最后求得的稳定安全系数值。进行边坡稳定分析的目的，就是要找出所有既满足静力平衡条件又满足合理性要求的安全系数解集，而且确认这个解集的上、下限非常接近，从工程实用角度看，只相当于这个解集的一个点，这个点就是所分析土坡的稳定安全系数，这样的求解方法被称为“严格解”。
但必须指出，采用极限平衡方法来分析边坡稳定，由于没有考虑土体本身的应力-应变关系和实际工作状态，所求出的土条之间的内力或土条底部的反力均不能代表土坡在实际工作条件下真正的内力或反力，更不能求出变形。我们只是利用这种通过人为假定的虚拟状态来求出安全系数而已。由于在求解中做了许多假定，不同的假定求出的结果是不同的。因此，实际上并不存在1个“精密解”。
大量计算资料表明，对于基于极限平衡理论的各种稳定分析方法，当采用的滑裂面为圆柱面时，尽管求出的Fsmin各不相同，但最危险滑弧的位置却很接近，而且在最危险滑弧附近，FS值的变化很不灵敏。因此，完全可能利用最简单的瑞典圆弧滑动法来确定最危险滑弧的位置，然后对最危险滑弧或再加上附近少量的滑弧，用比较严格但又比较复杂的方法来核算它的安全系数，这样可使计算工作重大为减少。
下面简述“条分法”的计算方法：
滑动面通过坡脚；在计算中当作平面问题看待。
计算时，按比例绘出边坡剖面（图2.2），任选一圆心O，以Oa为半径作圆弧，ab为滑动面，将滑动面以上土体分成几个等宽（不等宽亦可）土条。设土条自重（包括土条顶面的荷载）Wi，为简化计算，以土条侧面上的法向力pi、pi+1，和剪力Xi、Xi+1，的合力相平衡，则作用于滑动面fg上的法向反力Ni和剪切力Ti分别为：
构成滑阻力的还有黏聚力Ci，则滑动面ab上的总滑
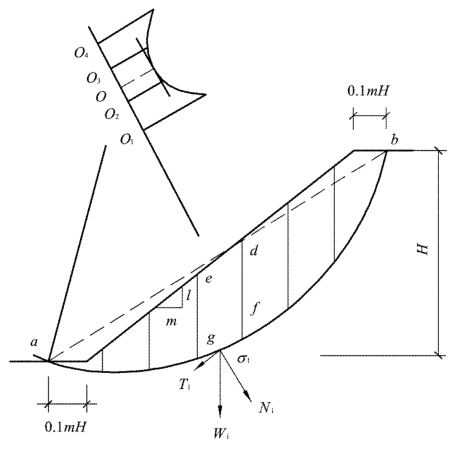
图2.2 土坡剖面
动力矩为
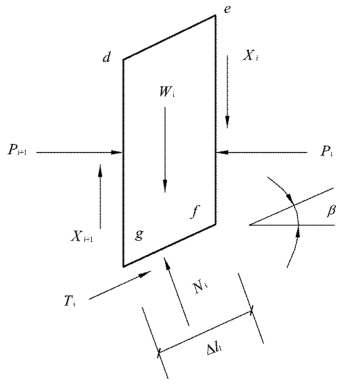
图2.3 作用于土条上的力
边坡稳定系数K为
式中 Κ——边坡稳定安全系数，一般取1.25～1.43；
li——分条的圆弧长度；
φi——分条土的内摩擦角；
βi——分条的坡角；
R——滑动圆弧的半径；
T——滑动面上总滑动力；
T'——滑动面上总阻滑力。
如果有地下水，则需考虑孔隙水压力u的影响，则按下式计算边坡稳定安全系数：
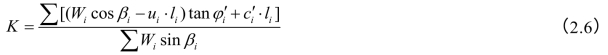
式中 c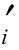
、φ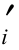
——有效内聚力和有效内摩擦角；
ui——分条土的孔隙水压力。