2.1.3 简布的普遍条分法
1.普遍条分法的基本假定和计算公式
图2.7所示:是土坡断面最一般的情况,土坡面是任意的,上面作用着各种荷载,剪切面(滑裂面)也是任意的。推力线是指土条两侧作用力(条间力)合力作用点位置的连线。在整个土坡的两侧作用着侧向的推力Ea、Eb和剪力Ta、Tb。
如果在土坡断面中任取一土条,如图2.8所示,其上作用着集中荷载ΔP、ΔQ及匀布荷载q,ΔWγ为土条自重,在土条两侧作用有条间力T、E及T+ΔT、E+ΔE,ΔS及ΔN则为滑裂面上的作用力。一般来说,T、E、ΔS及ΔN为基本未知量。
为了求出一般情况下土坡稳定的安全系数以及滑裂面上的应力分布,可以采用简布的普遍条分法(GPS法)在平面应变问题的条件下,简布做了如下假定。
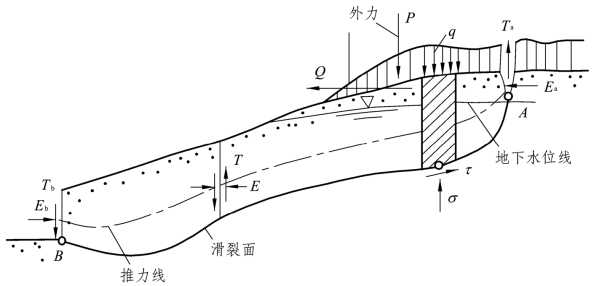
图2.7 简布法计算图式
(1)整个滑裂面上的稳定安全系数是一样的,其定义表达式为式(2.18),

(2)土条上所有垂直荷载的合力ΔW=ΔWγ+qΔx+ΔP,其作用线和滑裂面的交点交点与ΔN的作用点为同一点。
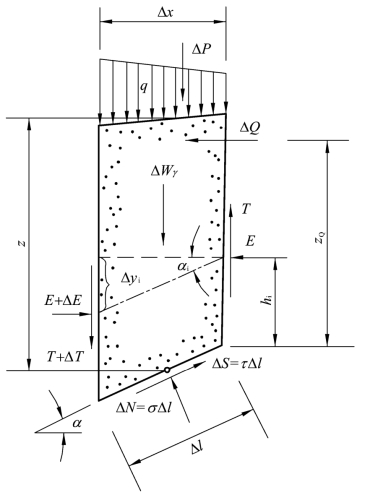
图2.8 土条上的作用力
(3)推力线的位置假定已知。根据土压力计算理论,可以简单地假定土条侧面推力成直线分布,如果坡面没有超载,对于非黏性土(c′=0),推力线应选在(或靠近)土条下三分点处;对于黏性土(c′>0)则在这点以上(被动情况)或这点以下(主动情况)。如果坡面有超载,侧向推力成梯形分布,推力线应通过梯形的形心。
简布假定ΔW和ΔN的作用点是同一点,这是不大合理的,但其影响在推导公式中属于二阶微量,可予忽略。至于推力线位置的变化,主要影响着土条侧向力的分布,对安全系数的影响很小。
对于每一土条,根据所假定的滑裂面,可以量得滑裂面坡度tanα及土条宽ΔX。单位土条宽度上作用的总垂直荷载为![]() 式中γ为土的容重。水平荷载为ΔQ,其作用点位置力滑裂面的距离为ZQ。当推力线位置确定以后,尚可量得推力线与滑裂面的垂直距离ht及推力线的坡度tanαt。
式中γ为土的容重。水平荷载为ΔQ,其作用点位置力滑裂面的距离为ZQ。当推力线位置确定以后,尚可量得推力线与滑裂面的垂直距离ht及推力线的坡度tanαt。
根据力及力矩平衡条件,对每一土条,可列出下列四个基本方程,即
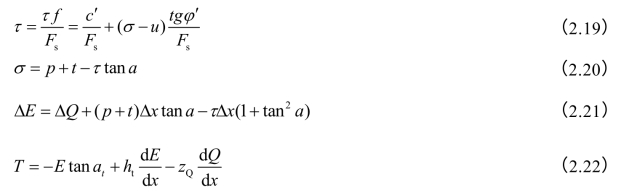
式(2.19)是滑裂面上的平衡条件,u为滑裂面上的孔隙应力;式(2.20)是力的垂直平衡方程,式中t=ΔT/Δx;式(2.21)是力的水平平衡方程,其中σ是用式(2.20)代入消去的;式(2.22)则是根据力矩平衡条件得出的,式中Δx的高次项已略去。对于整个滑动土体,整体的水平作用力平衡要求;
∑ΔE=Eb-Ea
将式(2.21)代入上式,得
![]()
根据假定,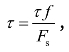 代入上式,得
代入上式,得
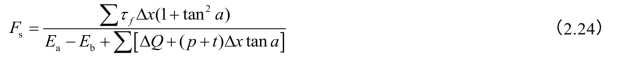
而
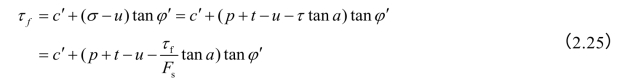
因为式子两边均包含有Fs项,须用迭代法试算。
由式(2.25)得

为了使公式简化,引入

将式(2.26)代入式式(2.27)并令

由式(2.30)已制成![]() 的关系曲线以备查用。
的关系曲线以备查用。
简化以后成为

滑裂面上的剪应力τ可由是式(2.27)求出,即

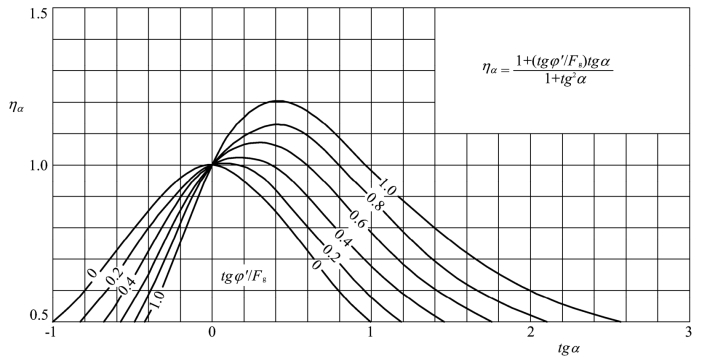
图2.9 ηa曲线图
正应力σ则直接由基本方程式式(2.20)求得。
必须指出,在上列各式中,T及t=ΔT/Δx 是未知的。谦为了求解T及t得

每一土条侧向水平作用力可由A点开始(见图2.9),从上往下逐条推求,即
E=Ea+∑ΔE (2.35)
求出E以后,T即可由基本方程式(2.22)求得,当土条两侧的T均已知时,该土条的ΔT及t就很容易求出来了。但因为求M、N的式(2.27)及式(2.28)中均含有t项,所以t并不能直接解出,也必须用迭代法来解决。
用普遍条分法不仅可以求出沿滑裂面的平均安全系数FS及滑裂面上应力σ及τ的分布,还可以求出各土条分界面上抵抗剪切的安全系数Fu,作为校核之用。
因为各土条分界面上的作用力E及T已经求出,如果分界面的长度为z,则分界面上平均的水平向应力为![]() 垂直向(切向)应力为
垂直向(切向)应力为![]() σh可假定沿界面呈直线分布,若E的作用点位于下三分点,则分布图形为三角形,否则为梯形。若分界面上的总孔隙水应力为Uh(方向水平),平均孔隙应力为
σh可假定沿界面呈直线分布,若E的作用点位于下三分点,则分布图形为三角形,否则为梯形。若分界面上的总孔隙水应力为Uh(方向水平),平均孔隙应力为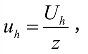 则(https://www.daowen.com)
则(https://www.daowen.com)

式中,c′及φ'要用分界面上的平均强度指标。一般来说,Fu≥FS。
2.普遍条分法的计算步骤
应用普遍条分法的具体计算步骤如下。
(1)假定滑裂面,划分土条,求出各土条的tanα、Δx、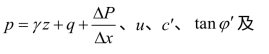 ΔQ。
ΔQ。
(2)假定t0=0,求出
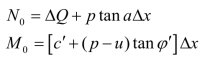
(3)先假定ηα0=1,则M0=M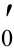 ,而
,而
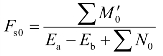
(4)由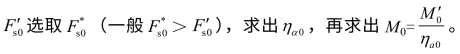
(5)再由MO、NO求出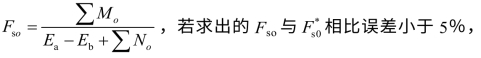
可选用,否则重新假定![]() 重新计算。
重新计算。
(6)当t0=0时,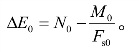
(7)求出各土条分界面的Eo,从坡顶逐条往下椎,E0=Ea+∑ΔE0,直到最后满足条件Ea-Eb=+∑ΔE0。
(8)根据推力线位置求出tanαt、ht、zQ。
(9)由下式求![]()
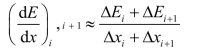
(10)求得各土条分界面上第一个近似的T值。
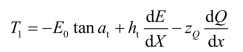
(11)求出每一土条的ΔT值。
ΔTi=Ti,i+1-Ti,i-1
(12)求出每一土条的t值。
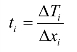
(13)求出
N1=N0+ΔT tan α
![]() 这是M、N的第一次近似值。
这是M、N的第一次近似值。
(14)由Fso假定![]() 求出各土条的ηα1。
求出各土条的ηα1。
(15)求得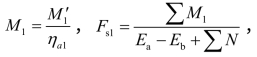 若Fs1与
若Fs1与![]() 相比误差小于5%,可选用,否则重新假定
相比误差小于5%,可选用,否则重新假定![]() 重新计算。
重新计算。
(16)重复步骤(6)~(15),从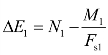 开始,直到算出安全系数的第二次近
开始,直到算出安全系数的第二次近
似值Fs2,将Fs2与Fs1比较,若符合精度要求,则迭代结束,取Fs=Fs2,否则继续迭代,一般仅需迭代3次。
(17)当Fs,确定以后,由式(2.20)、式(2.22)求出各土条滑裂面上的应力σ及τ,此时已得如下成果:沿滑裂面的平均安全系数Fs、所有土条分界面上的作用力E及T、每一土条底面的平均应力σ及τ。
(18)校核每一土条分界面上的抗剪安全系数Fu。
(19)绘制成果,计算结束。
因为普遍条分法通常用来校核一些形状比较特殊的滑裂面(如复杂的软土层面),所以不必要假定很多的剪切面进行计算。计算表格及算例可参阅赫兹费尔特及普鲁斯主编的《土石坝工程》一书中简布的有关文章。
3.王复来对简布法的改进
20世纪70年代末,王复来同志对简布的方法作了很有价值的改进,他从任一土条上各种作用力的极限静力平衡条件出发,导出了类似式(2.20)~式(2.23)这样一组基本方程式,由此可以求解ΔE、ΔT、ΔN、ΔS四个基本未知量。对第n条土条,如图(2.8),如果土条侧面的推力是由下往上逐条推算的,则土条左边的侧向力为Tn、En,右边的侧向力为Tn+1、En+1,ΔE及ΔT的正负号与普遍条分法相反。对基本方程式进行适当的换算、整理,可得到
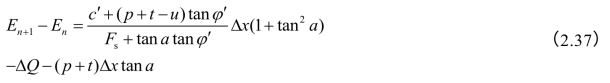
当土条宽度取得足够小时,可以认为Δx、ΔE、ΔT均趋近于零,如果在推导公式的过过程中再略去二阶微量,可以近似地求出
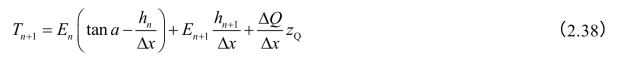
式中,hn及hn+1分别为土条两侧推力作用点离开土条侧面底部的距离,与前式是不完全一样的。经过整理,还可以求出
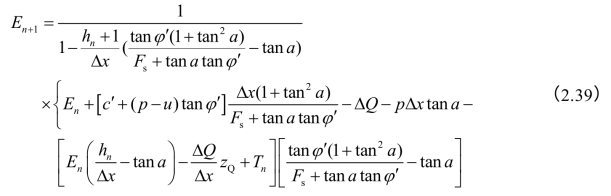
安全系数FS的式和式(2.24)完全相同,如果土坡两端没有外力,即Ea、Eb、Tb均等于零,同时假定土条划分为m条,则有
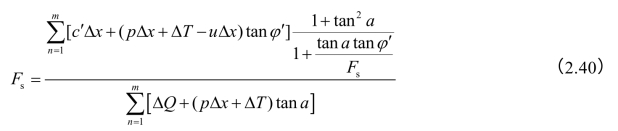
解题时可用试算法或迭代法。
试算法利用式(2.39),先假定一个FS,根据E1=0的初始边界条件,由下往上逐条推求各土条的侧向推力En+1,直至第m条,如果求出的Em+1=0,则所假设的安全系数即为所求,否则要另行假定FS重复计算;也可假设三个以上的FS,求出FS与Em+1的关系曲线,由Em+1=0求出所要求的FS值。
迭代法步骤要比普遍条分法简单一些。首先假设FS0,据初始边界条件E1=0、T1=0从下往上逐条推求侧向推力直至m-1号土条,分别求出E2、E3、…、Em及T2、T3、…、Tm;再根据Tm+1=0的条件,算得各土条的ΔT1、ΔT2、…、ΔTm;点用所设的Fs0及ΔT1、…、ΔTm代入式(2.40)算得安全系数的第一次近似值Fs1;核算Fs1与Fs0的相对误差是否满足精度要求,如不满足则以Fs1作为Fs0。重复上述步骤,直至相邻两次迭代计算得到的Fs值其相对误差满足要求为止。王复来法的基本出发点和普遍条分法是一样的,其计算精度也差不多,但使用起来却比普遍条分法方便。
