2.1.4 斯宾塞法
斯宾塞假定相邻土条之间的法向条间力E与切向条间力X之间有一固定的常数关系，即
因此各条间力合力P的方向是相互平行的。取垂直土条底部方向力的平衡，则
Ni+(Pi-Pi+1)sin(ai-θ)-Wicosai=0
再取平行土条底部方向力的平衡。
则
Ti-(Pi-Pi+1)cos(ai-θ)-Wisinai=0
同时根据安全系数的定义及摩尔—库伦准则，可得
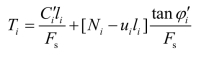
又li=bisecαi。综合上列各式，可求出土条两侧条间力合力之差为
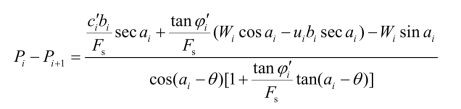
对整个滑动土体来说，为了要维持力的平衡，必须满足水平和铅直方向的平衡条件
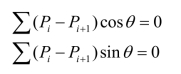
因为θ是个常数，sinθ和cosθ不可能为零。因此，上列两式实际上是同一个平衡条件，即
∑(Pi-Pi+1)=0 （2.42）
同样，对整个滑动土体，还必须满足力矩平衡条件，即
∑(Pi-Pi+1)cos(ai-θ)R=0 （2.43）
式中，R为各土条底部中点离转动中心的距离，如果取滑裂面为圆柱面，R就是圆弧的半径，而且对所有土条都是常数，上式可写成
∑(Pi-Pi+1)cos(ai-θ)=0 （2.44）
将式（2.41）分别代入式（2.42）及式（2.44），可得到两个方程，而当土坡的几何形状及滑裂面已定，同时土质指标又已知时，只有θ及FS两个未知数，问题因而得解。
斯宾塞法的具体解题步骤如下。
（1）任意选择一圆弧滑裂面，划分垂直土条，宽度相同，在图上量出土条中心高h及底坡a。
（2）选定若干个θ值，对于每一个θ值，都可求出不同的FS值以满足式（2.42）及式（2.44），用力的平衡方程式（2-42）得到的FS值以Fsf表示，而以力矩平衡方程式（2.44）求得的为FSm，当θ=0°时，用力矩平衡方程求得的安全系数称为FSm0，它相当于用简化毕肖普法求出的FS值。
（3）作出Fsf-θ及Fsm-θ关系曲线，绘于同一张图上，如图2-10所示，两条曲线的交点就给出了同时满足式的安全系数Fs及条间力的坡度θ。
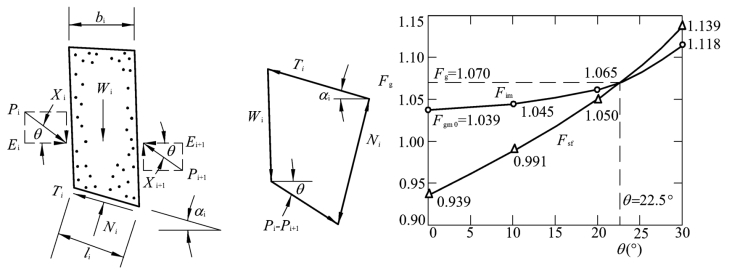
图2.10 斯宾塞法Fs-θ关系曲线
（4）以求出的F及θ，从上往下逐条求出每一土条两侧的条间力合力，井由此求出土条分界面上的法向力及剪力，然后根据分界面上土的强度指标，求出抗剪安全系数Fu。
（5）再从上住下逐条求出条间力合力作用点的位置，这可以通过对土条底部中点求力矩得出。
（6）重新选择滑裂面，重复上述步骤，以求得最危险的滑裂面位置及Fsmin值。
摩根斯坦-普赖斯首先对任意曲线形状的滑裂面进行了分析，导出满足力的平衡及力矩平衡条件的微分方程式，然后假定两相邻土条法向条间力和切向条间力之间存在1个对水平方向坐标的函数关系，根据整个滑动土体的边界条件求出问题的解答。
图2.11（a）表示一任意形状的土坡，其坡面线、侧向孔隙水应力和有效应力的椎力线及滑裂线分别以函数y=z（x）、x=h（x）、y=γ′t（x）及y=y（x）表示。图2.11（b）为其中任一微分土条，其上作用有重力dW，土条底面的有效法向反力dN′及切向阻力dT，土条两侧的有效法向条间力E′、E′+dE′及切向条间力X、X+dX。U及U+dU为作用于土条两侧的孔隙水应力，dUS则为作用于土条底部的孔隙水应力。
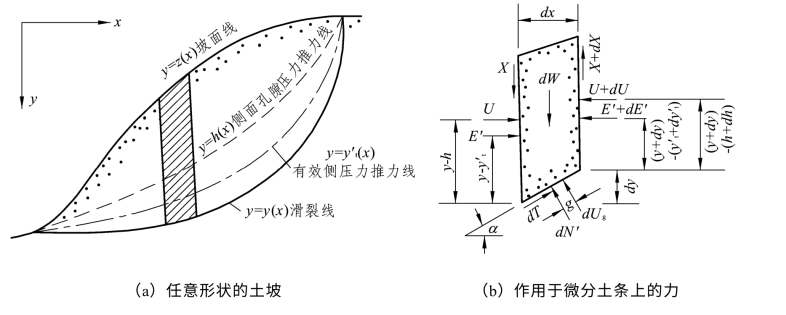
图2.11
对土条底部中点（dT、dN′合力作用点）取力矩平衡，则
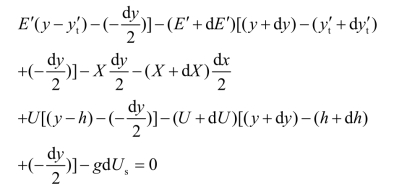
将上式整理化简，略去高阶微量，并且认为dUs的作用点与dT、dN′的作用点重合（取g=0），就得到每上一条满足力矩平衡的微分方程式
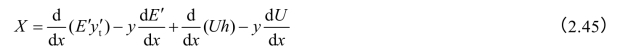
再取土条底部法线方向力的平衡，得
dN'+dUs=dW cos a-dX cos a-dE'sin a-dU sin a （2.46）
同时取平行土条底部方向力的平衡，可得
dT=dE'cos a+dU cos a-dX sin a+dW sin a （2.47）
又根据安全系数的定义及摩尔—库伦准则
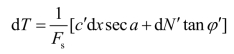
同时引用毕肖普等关于孔隙应力比，得
dUs=ru dW sec a （2.48）
综合以上各式，消去dT及dN′，得到每一土条满足力的平衡的微分方程为
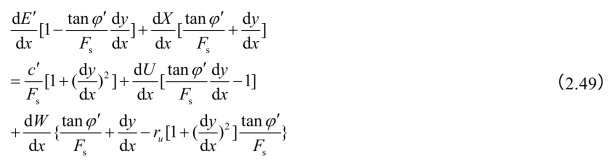
式中，Fs为稳定安全系数，ru为孔隙应力比。
一般来说，y=z（x）、y=h（x）是已知的，y=y（x）由我们选定，也是已知的，两个基本微分方程中的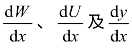
都可以求出，同时土质指标c′、tan φ′及孔隙压力比ru也是给定的。因此，要求的未知量就剩下E′、X及函数y=y′t（x），还有安全系数Fs。
为了简化方程，以土条侧面总的法向力E来代替有效法向力E′，则有
E=E′+U （2.50）
其作用点位置yt可用式（2.50）求出，即
Eyt=E′y′t+Uh （2.51）
同时因为E和X之间必定存在着1个对x的函数关系
X=λf(x)E （2.52）
式中，λ为任意选择的1个常数。
对每一土条来说，由于dx可以取得很小，使y=z（x）、y=h（x）及y=y（x）在土条范围内近似为一直线，同样，函数f（x）在每一土条范围内也可以取作直线。因此，在每一土条内有
及式中，A、B、p、q、k及m均为任意常数，可通过几何条件及所选f（x）的类型来确定。
经过式（2.50）～式（2.55）的处理，基本微分方程式简化为
进一步简化为
式中
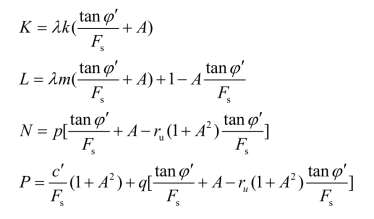
现在取土条西侧的边界条件为
E=Ei（x=xi）
E=Ei+1（x=xi+1）
从xi到xi+1进行积分，可以求得
这样就可以从上到下，逐条求出法向条间力E来，然后根据式（2.52）求出切向条间力X。当滑动土体外部没有其他外力作用时，对最后一土条必须满足条件
En=0 （2.59）
同时，土条侧面的力矩可以用微分方程式（2.56）积分求出，即
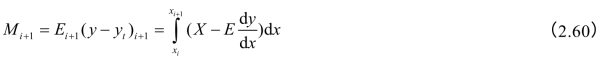
最后也必须满足条件
此时，各条间力合力作用点位置yt可由式（2.60）求出。
因此，为了找到满足所有平衡方程的λ及Fs值，我们可以先假定一个λ及Fs，然后逐条积分得到En及Mn，如果不为零，再用一个有规律的迭代步骤不断修正λ及Fs，直到式（2.59）及式（2.61）得到满足为止。
最后剩下的问题是f（x）如何选择的问题，他们可以利用弹性理论的解答加以算出，也可以在直观假设的基础上指定。根据摩根斯坦等人的研究，对于接近圆弧的滑裂面，安全系数对内力分布的反应是很不灵敏的，往往取完全不同的f（x），得到的安全系数却相当接近。
当然，用本法求出的条间力也必须符合第一节提到的合理性条件（土条分界面上抗剪安全系数Fu≥Fs及不存在拉力），如果这两个条件得不到满足，可以通过修改f（x）来加以调整。
摩根斯坦—普赖斯法是对土坡稳定进行极限平衡分析计算的最一般的方法。
整个滑动土体还要满足力矩平衡的条件，现取所有作用力均对滑动土体的重心G取力矩，则Wi及KWi其力矩总和为零，而条间力X、E是滑动土体的内力，也不产生力矩，这样就得到
∑(Ticos ai-Nisin ai)(yi-yg)+∑(Nicos ai+Tisin ai)(xi-xg)=0 （2.62）
在上式中消去Ni及Ti得力矩平衡方程为
∑(Xi+1-Xi)[(yt-yg)tan(φ'-ai)+(xi-xg)]=∑Wi(xi-xg)+∑Di(yi-yg) （2.63）
在式（2.62）、式（2.63）中，只有地震加速度K及条间力X是未知的，如果我们能够找到X 的表达式同时满足式（2.63）及∑（Xi+1-Xi）=0，则由式（2.62）就可以求出K，此时的K也就是临界地震加速度Kc。
为此，沙尔玛假定
Xi+1-Xi=λFi （2.64）
式中，λ为一常数；Fi是一待求的函数，当然必须满足∑Fi=0。
将式（2.64）代入式（2.62）及式（2.63），并解此联立方程组，得
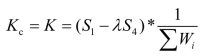
其中
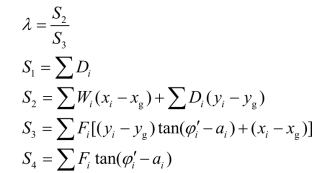
当Xi+1-Xi为已知时，可以由式（2.58）求出（Ei+1-Ei），然后从边界开始逐条推求各土条分界面上的Ei及Xi，从而求出土条分界面上的抗剪安全系数为
式中，Upi为作用于土条侧面的孔隙水应力，c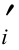
及tanφ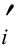
可以用土条侧面各土层的加权平均抗剪强度指标。Ei的作用点位置可以取每一土条各作用力对土条底面中心求力矩，得
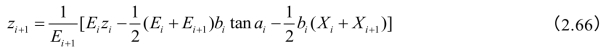
同样可从初始条件Zi开始逐条堆求。
最后剩下的问题是Xi或Xi如何确定，沙尔玛已经堆求出均质和非均质情况下Xi的表达式，对于均质的情况可用下式表示，即
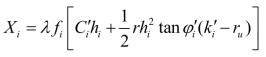
其中
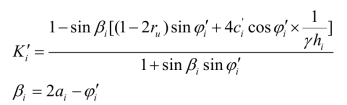
fi是可以任意选择的值，通常可取fi=1，如果求出的Fui＜1或条间力作用点位置超出三分点，可以通过修正fi加以调整。
这是我国工民建和铁道部门在核算滑坡稳定时使用非常广泛的方法。它同样适用于任意形状的滑裂面，而假定条间力的合力与上一条土条底面相平行，根据力的平衡条件，逐条向下推求，直至最后一条土条的推力为零。
图2.12是任意一滑动土条，其两侧条间力合力的作用方向分别与上一条土条底面相平行，取垂直与平行土条底面方向力的平衡，有
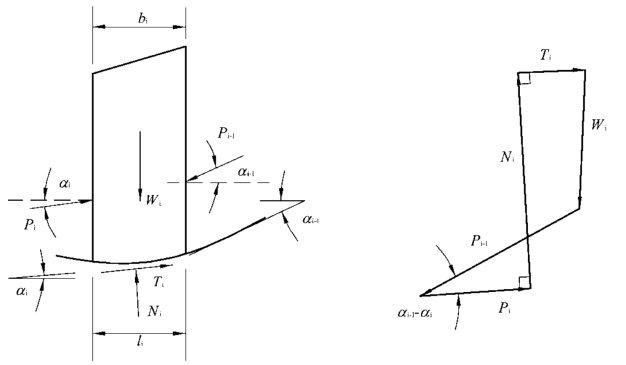
图2.12
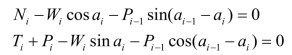
应用安全系数的定义及摩尔-库伦准则，得
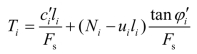
式中，Ui为作用于土条底面的孔隙应力。
由以上三式消去Ti、Ni，得
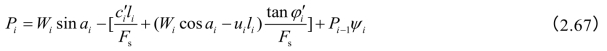
式中ψi称为传递系数，以式（2.68）表示，即
在解题时要先假定Fs，然后从第一条开始逐条向下椎求，直至求出最后一条的推力Pn，Pn必须为零，否则要重新假定Fs进行试算。
为了使计算工作更加简化，在工程单位常采用下列简化公式，即
Pi=FsWisinai-[c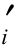
li+(Wicosai-uili)tanφ
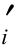]+Pi-1ψi （2.69）
式中，传递系数ψi改用下式计算，即
ψi=cos(ai-1-ai)-tanφ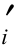
sin(ai-1-ai) （2.70）
如采用总应力法，在式（2.69）中略去uil项，c、φ值可恨据土的性质及当地经验，采用试验和滑坡反算相结合的方法来确定。Fs值应根据滑坡现状及其对工程的影响等因素确定，一般可取1.05～1.25。另外，因为土条之间不能承受拉力，所以任何土条的推力pi如果为负值，则此pi不再向下传递，而对下一条土条取pi-1=0。
各土条分界面上的pi求出之后，就很容易求出此分界面上的抗剪安全系数，为一常数，其结果和斯宾塞相同；更特殊一些取f（x）=0，则相当于简化毕肖普法。
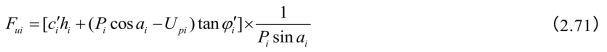
我国水利水电科学研究院陈祖煜在摩根斯坦指导下，对这个方法作了改进。首先，从以上列出的静力平衡微分方程出发，结合相应的边界条件，推导出下列带有普遍意义的极限平衡方程式。对力的平衡，有
对力矩平衡则有
其中
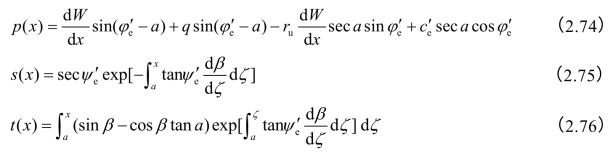
式中，q为坡面垂直荷载，ru为孔隙应力比，β为土条侧向作用力合力对x轴的倾角a、b为滑弧两端的x坐标，ζ、ξ则为积分变量。c
、φ
、ψ
分别用以下各式求出，其余符号同前。
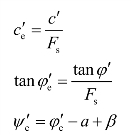
不难看出，在式（2.72）、式（2.73）中，p（x）表示土条底部各作用力在底面合力垂直方向上的分量；ψ
表示此方向与土条侧向作用力合力方向的交角；而∫p（x）s（x）dx 是在土条侧向作用力合力方向上力的平衡；t（x）则是垂直于土条侧向作用为合力方向的力臂。
在式（2.72）、式（2.73）中仅有β（x）及Fs是未知量，在满足合理性要求的前提下，可任意假定以β（x），代入两式中求Fs，这些都是满足静力极限平衡条件的解答[如假定β（x）为常量，就是斯宾塞法，假定β（x）=0就变成简化毕肖普法等）。但需注意，β（x）在滑动土体两个端部的土条上是1个确定值，需满足端部土条力的平衡合理性条件。根据陈祖煜的研究，如果端部条块形状是个三角形，而且其宽度取得足够小的话，β应等于端点处土坡面的倾角，亦即端部条块侧面总作用力应平行于该土条土坡面的方向。
假定一个β（x）的分布形状，解式（2.72）、式（2.73），求出满足方程组的解答β*（x）和Fs*，这就是摩根斯坦—昔赖斯法。陈祖煜对该法的电算程序做了改进，加了相应的功能，使端点的β（x）能满足确定的要求，采用了多种数值计算的技巧，以保证计算程序的收敛性。在求得β*（x）和
以后，还可以求出同样满足式（2-63）、式（2-64）的邻近解β*（x）+Δβ和Fs*+ΔFs。采用这个步骤，有意识地改变β*（x）的形状分布，使原来满足合理性要理性要求的解过渡到不满足合理性要求的解，以发现向这一方向过渡的边界。然后变换过渡方向，用同样步骤，求出另一方向满足合理性的边界。相应于这两个边界的Fs值，就是安全系数的上、下限。如果这两个数值的确非常接近，就求出了相应于这个滑裂面的土坡稳定安全系数的“严格解”。