2.1.2 毕肖普法
毕肖普考虑了条间力的作用，并按照式（2.1）关于安全系数的定义，在1955年提出了一个安全系数计算公式。如图2.4所示，Ei及Xi分别表示法向及切向条间力，Wi为土条自重，Qi为水平作用力，Ni、Ti分别为土条底部的总法向力（包括有效法向力及孔隙应力）和切向力，其余符号见图2.4。根据每一土条垂直方向力的平衡条件有
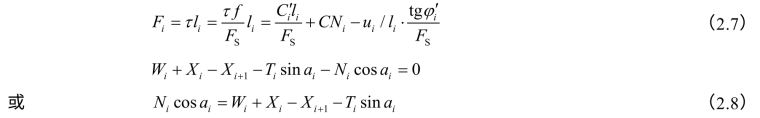
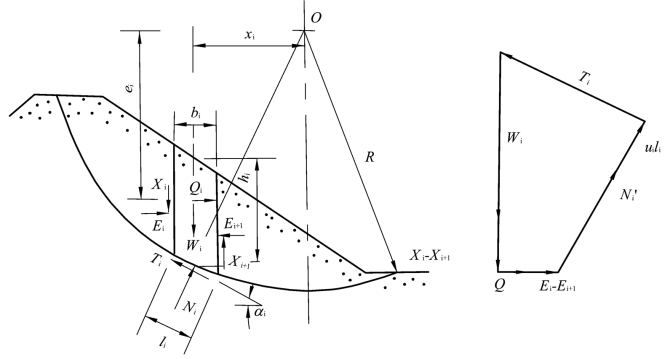
图2.4 毕肖普法
按照安全系数的定义及摩尔—库伦准则，Ti可用式（2.7）表示，代入式（2.8），求得土条底部总法向力为：
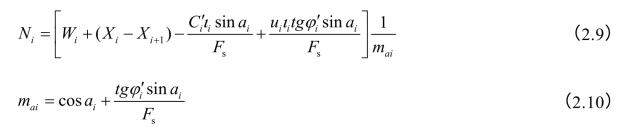
在极限平衡时，各土条对圆心的力矩之和应当为零，此时条间力的作用将相互抵消。因此，得
将式（2.7）、式（2.9）代入式（2.11），且Xi=R sin αi，最后得到安全系数的公式为
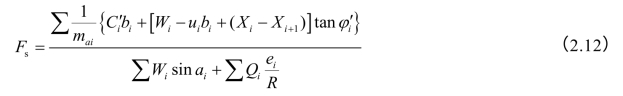
式中，Xi及Xi+1是未知的，为使问题得解，毕肖普又假定各土体之间的切向条间力均略去不计，也就是假定条间力的合力是水平的，这样式（2.12）。
可简化成
这就是国内使用相当普遍的简化毕肖普法。因为在mα内也有FS这个因子，所以在求FS时要进行试算。在计算时，一般可先假定FS=1，求出mα（或假定mα=1），再求FS，再用此FS，求出新的mα及FS，如此反复迭代直至假定的FS和算出的FS非常接近为止，根据经验，通常只要迭代3～4次就可满足精度要求，而且迭代通常总是收敛的。
必须指出：对于αi为负值的那些土条，要注意会不会使mα趋近于零，如果是这样，则简化毕肖普法就不能用。这是由于既在计算中略去了Xi的影响，又要今各土条维持极限平衡，在土条的αi使mα趋近于零时，Ni就要趋近于无穷大，当的绝对值更大时，土条底部的Ti将要求和滑动方向相同，这是与实际情况相矛盾的。根据某些学者的意见，当任一土条其mα≤0.2时，就会使求出的FS值产生较大的误差，此时就应考虑Xi的影响或采用别的计算方法。
为了考虑Xi的影响，除了采用以下各节介绍的方法外，也可以用式（2.12）。对于比较平缓的均质土坡，式中Xi-Xi+1值可以用潘家铮根据弹性理论锥求出来的简化式（2.13）加以估算，即
式中β是土坡的坡角，Kβ是一个系数可用下式计算
式中，a、b为与坡角β有关的两个系数，中给出了它们的值，γ为泊松比
值大致在0.6～1.0之间变化。Xi力沿水平轴的分布，一般呈两端为零、中央凸出的曲线形，从而在边坡顶部几个土条的（Xi-Xi+1）值一般为负，而靠近边坡出口处则常常为正。而且因为Xi是各土条之间的内力，对整个土体来说，必须满足∑（Xi-Xi+1）=0的条件。
为了能迅速求出用有效应力分析得到的最小稳定安全系数，毕肖普和摩根斯坦在1960年提出了稳定系数法。他们应用简化毕肖普法对没有戗道的均质土坡进行了分析，认为对一定的抗剪强值，土坡最小稳定安全系数Fsmin与整个土坡断面的平均孔隙应力比ru接近于直线关系，见图2.5，即
Fsmin=M=Nru
式中孔隙应力比ru是用下式定义的，即
其中 u——土坡断面中某一点的孔隙应力；
h——该点至坡面垂直距离；
γ——土的容重。
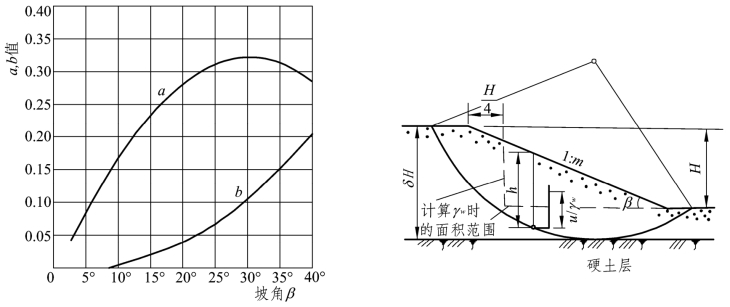
图2.5 系数a，b值ru计算范围
地基与填方土质无显著差别时，最危险滑裂面也可能深入坝基内，此时并无明显的硬土层存在。有的硬土层埋藏很深，最危险滑裂面底部不一定与它相切，为此，需要利用图2.6中以虚线表示的等rue线，求出最危险滑裂面的深度因素δ，再由这个δ来求出稳定系数M、N。此时对于给定的一组参数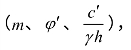
必有一个孔隙应力比使δ比较低时的安全系数与δ比较高时的安全系数相等。这一孔隙应力比即以rue。表示为
式中 M2、N2——由比较深的δ求出的稳定系数；
M1、N1——由比较低的δ求出的稳定系数。
当一个土坡的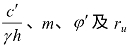
值已经确定，可以先由
根据m及φ'查图上的虚线，得到相应的rue，如果rue＜ru，则说明δ=1.25时的安全系数比δ﹦1.0时为低，需要利用δ﹦1.25的图进一步检查，直到求出的rue＞ru，则相应的δ就是最危险滑裂底部经过的那个深度因素，可由此查得M、N并算出Fsmin。
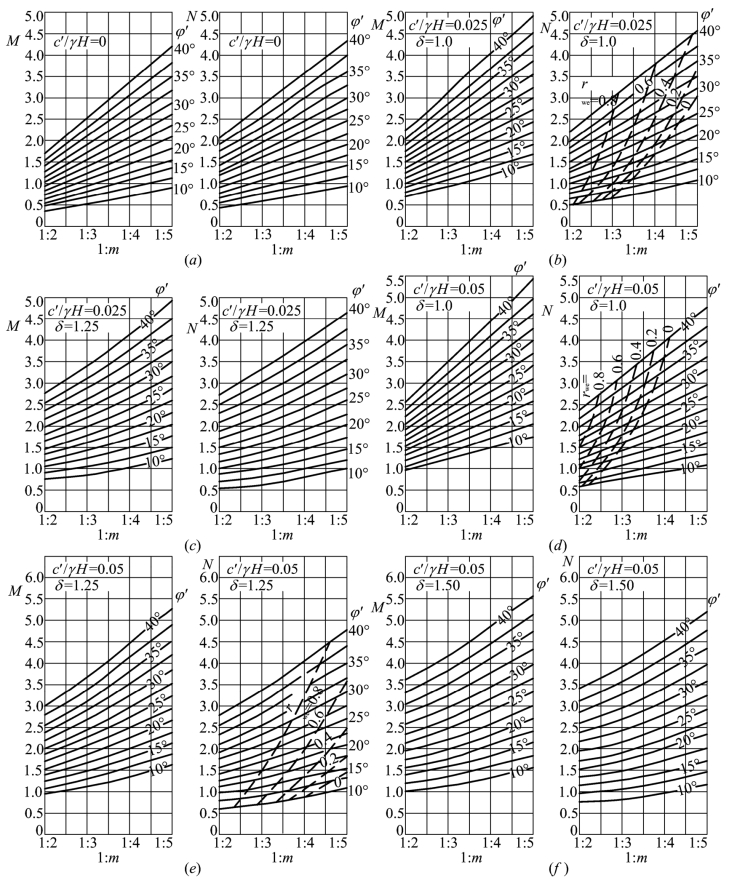
图2.6 m、φ'、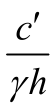
参数
例如：某均质土坡，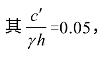
坡比为1∶4，φ'﹦30°，设计的ru=0.5，第一层硬土层的深度因素δ=1.43，求最小稳定安全系数Fsmin。
解：（1）由
m﹦4，φ'﹦30°查图2-5（d），得δ﹦1.0时rue＜0.5，因此δ﹦1.0，不是最危险滑裂面底部所在深度。
（2）同样由
m=4，φ'=30°查图，得δ=1.25时，ru=0.72，因为rue＞ru，所以虽然实际的δ﹦1.43，但最危险滑裂面底部的深度因素却为δ=1.25。
（3）由图查出M=3.2，N﹦2.8。
（4）计算Fsmin。
Fsmin=3.2-2.8*0.5=1.8