2.4.1 基坑开挖
1.基坑边坡及其稳定
基坑边坡坡度是以高度（H）与底宽（B）之比表示，即：
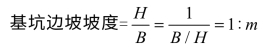
根据《土方和爆破工程施工及验收规范》的规定，当地质条件良好，加低于基坑（槽＞或管沟底面标高时，挖方边坡可作成直立壁而不加支撑，但深度按照下列规定：
密实、中庸的砂土和碎石类土——1.0 m；
硬塑、可塑的粉土及粉质黏土——1.25 m；
硬塑、可塑黏土和碎石土（填充物为黏性土）——1.5 m；
坚硬的黏土——2.0 m。
表2.6 深度在5 m内基坑，边坡的最陡坡度
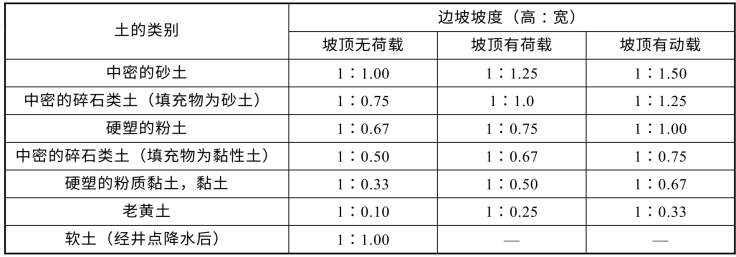
挖土深度超过上述规定时，应考虑放坡或作成直立壁加支撑。当地质条件良好，土质均匀且地下水位低于基坑（槽）或管沟底面标高时，挖方深度在5 m内不加支撑的边坡的最陡坡度应符合表2.6规定。
深度在5 m内的基坑（槽）、边坡的最陡坡度（不加支撑）。
引起土体剪应力增加的主要因素有：坡顶堆物、行车；基坑边坡太陡；开挖深度过大或地面水渗人士中；地下水的渗流产生一定的动水压力，土体竖向裂缝中的积水产生侧向静水压力等。
引起土体抗减强度降低的主要因素有：土质较差或因气候影响使土质变软；土体内含水量增加而产生润滑作用；饱和的细砂受到振动而液化等。
由于影响基坑边坡稳定的因素多，在一般情况下开挖深度较大的基坑应对土方边坡做稳定分析，即在给定的荷载作用下，土体抗剪切破坏应有一个足够的安全系数，而且其变形不应超过某一容许值。边坡稳定的分析方法很多，如条分法、摩擦圆法、极限分析法等。
2.最简单的条分法——瑞典圆弧滑动法
（1）瑞典圆弧滑动法的基本概念和计算方法。
瑞典圆弧滑动法，（简称瑞典法或费伦纽斯法）是条分法中最古老而又最简单的方法。除了假定滑裂面是个圆柱面（剖面图上是个圆弧）外，还假定不考虑土条两侧的作用力，安全系数定义为每一土条在滑裂面上所能提供的抗滑力矩之和与外荷载及滑动土体在滑裂面上所产生的滑动力矩和之比。由于不考虑条间力的作用，严格地说，对每一土条力的平衡条件是不满足的，对土条本身的力矩平衡也不满足，仅能满足整个滑动土体的整体力矩平衡条件。由此产生的误差，一般使求出的安全系数偏低10%～20%，这种误差随着滑裂面圆心角和孔隙压力的增大而增大。
瑞典圆弧法的推导：一般教科书上均有叙述，它通常采用总应力法。但同样可用有效应力计算井按式定义的安全系数来推导公式，为了考虑条间力的作用，井可认为假定每一土条两侧作用力的合力方向均和该土条底面平行，因而在进行土条底部法线方向力的平衡时，可以不予考虑。但是这个假定会使牛顿“作用力等于反作用力”的原理在两个土条之间得不到满足。
表示一均质土坡及其中任一土条i上的作用力。土条高为hi，宽为bi，Wi为其本身的自重；Pi及Pi+1为作用于土条两侧的条间力合力，其方向和土条底部平行；Ni及Ti分别为作用于土条底部的总法向反力和切向阻力土条底部的坡角为αi，长为li，R则为滑裂面圆弧的半径，如图2.13。根据摩尔一库伦准则，滑裂面AB上的平均抗剪强度为
τf=C'+(σ-μ)tan φ'
式中 σ——法向总应力；
μ——孔隙应力；
C′、φ'——有效抗剪强度指标。
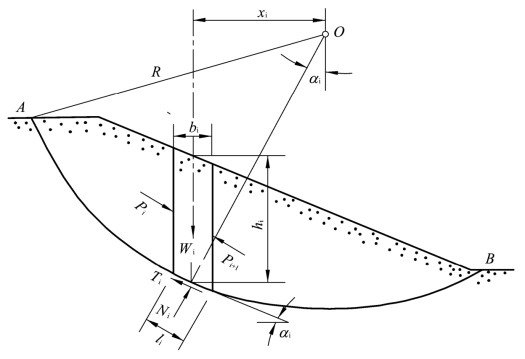
图2.13
如果整个滑裂面AB上的平均安全系数为FS，土条底部的切向阻力Ti为
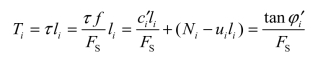
现取土条底部法线方向力的平衡，可得
Ni=Wicosαi
同时，各土条对圆心的力矩和应当为零，即
∑Wixi-∑TiR=0
而xi=R sin αi，得
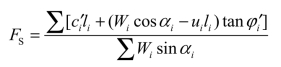
通常根据两个力矩和之比导出的公式完全相同。
当土坡内部有地下水渗流作用时，滑动土体中存在渗透压力，必须考虑它对土坡稳定性的影响。在滑动土体中任取一土条i，如果将土和水一起作为脱离休来分析，土条重量Wi就等于bi（γh1i+γmh2i）其中γ为土的湿容重，γm为饱和容重；在土条两侧及底部都作用有渗透水压力。在稳定渗流情况下，土体通常均已固结。由附加荷重引起的孔隙应力均已消散，土条底部的孔隙应力ui也就是渗透水压力，可用流网确定。如果经过土条底部中点M的等势线与地下水面交于N，则
ui=γwhwj
式中 γw——水的容重；
hwj——MN的垂直距离。
若地下水面与滑裂面接近平行，或土条取得很薄，土条两侧的渗透水压力接近相等，可相互抵消。
将上述结果代入式，又因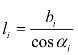
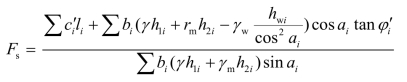
现在将式和目前工程单位普遍使用的替代容重法进行比较，后者的安全系数表达式为
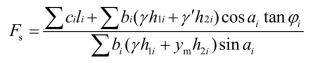
式中，γ′为土的浮容重，ci、φi用固结排水剪指标。可以看出，必须使分子中的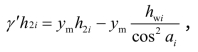
亦即
才能求出与相同的Fs，而这一点一般是不容易做到的。因此，替代容重法虽然是一个使用非常方便的简化方法，但有其一定的限制条件，如果在任何情况下均按此处理，有时会造成相当大的误差，而且往往还是偏于不安全的，如图2.14。
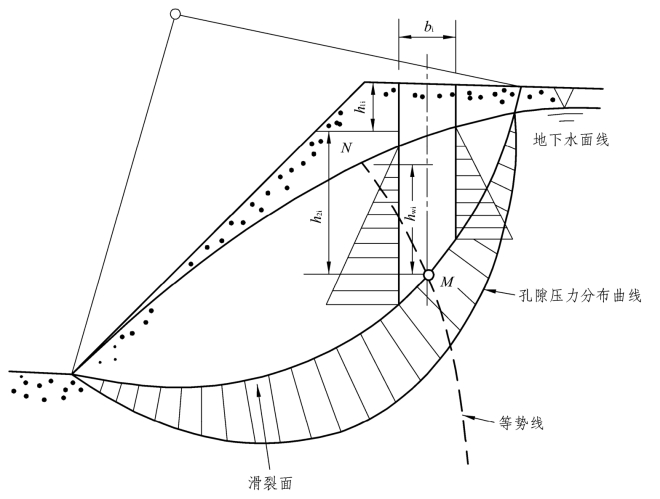
图2.14 渗流对土坡稳定的影响
必须指出，在稳定分析中，安全系数的定义通常有两种：一种是通过加大外力以达到极限平衡，这样的安全系数有超载系数的性质；另一种是降低材料的强度以达到极限平衡，求出的安全系数则是材料强度的储备系数。一般来说，零这两种安全系数的概念不一样，求出的结果也是不一样的。费伦纽斯在推导瑞典圆弧滑动法的公式时，所做的假定是用附加外力使土坡达到极限平衡，而我们以上的推导采用了式所定义的安全系数概念，很明显，它是属于强度储备系数性质的。两者求出的结果完全相同，是由于假定条间力合力方向与底面平行，当应力状态向极限平衡状态变化时，无论滑裂面上的剪阻力怎么变化，从多边形得出的法向反力却始终不变。因此，无论采用附加外力还是采用降低强度使土坡达到极限平衡，其结果是一样的。
另外，如果土坡中存在比较高的孔隙应力时，可能会产生很大误差，这是由于在推求法向反力Ni时，将包含在竖向总应力中一个应该各向同样大小的孔隙应力分量，也分解到法线方向上去了，这样就使得土条底部的法向有效应力偏低。正确的法向有效应力的合力N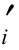
应当是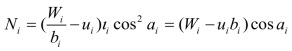
应改写成tanφ/tanβ。则最危险沿弧在无限深处。这些结论与费伦纽斯、泰勒等人曾经得到的结论是一致的。
（2）最危险滑弧圆心位置随s变化的轨迹，近似于双曲线的一侧，此双曲线的原点位于边坡中点，以过中点的铅垂线与中法线为其淅近线，如图2.15所示。潘家铮则认为可过边坡中点，分别以L/2及3L/4为半径作弧交中法线与中垂线于a、a′、b、b′，则最危险滑弧圆心的大致范围，当在aa′bb′之内。
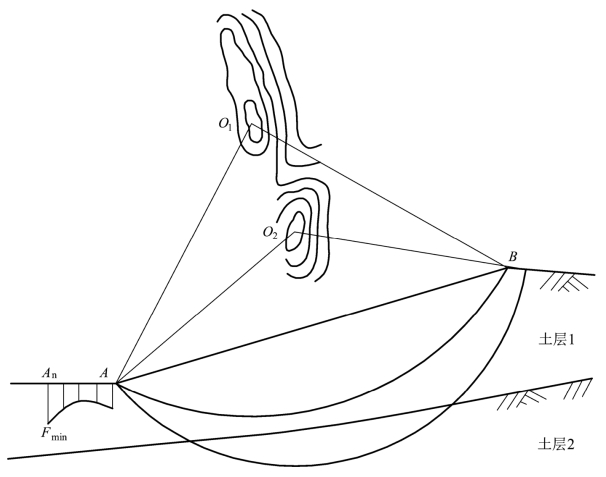
图2.15 不同土层的Fs极小值区
对于具有不同土层或有地下渗流等复杂情况的复杂土坡，最危险滑弧圆心位置和各土层的s有关。因此，有多少层土层（包括同一土层在地下水位线上下的不同部分）就可能出现多少个Fs的极小值区，尽管有时有些土层的Fs极小值区不十分明显。如图7-5所示，两个不同土层Fs最小的滑弧圆心分别为O1及O2。必须将所有极小值区的Fs进行比较，从中选择最小的Fs作为整个土坡的稳定安全系数。另外，对于复杂土坡，在计算时，要先固定一个出滑点：（如图中的A，……An），所有计算的滑弧均要通过同一出滑点，求出最小的Fs，再换另一个出滑点，最后对不同出滑点的Fsmin进行比较，从中求出最小的Fsmin。当然这些工作都可以通过编制程序在电子计算机中自动进行。目前各单位编制的有关土坡稳定计算的电算程序极多，使用时要注意是否考虑了上述最危险滑弧的分布规律，防止将真正的Fsmin漏掉。
由于滑动圆弧是任意选定的，所以上述计算结果不一定是最危险的，因此还必须对其他滑动圆弧（不同圆心位置和不同半径）进行计算，直至求得最小安全系数。而最小安全系数对应的滑弧即为最危险滑弧。根据经验，最危险滑弧两端距坡顶点和坡脚点各为0.1 mH处，且最危险滑弧中心在ab线的垂直平分线上。这样，只需在此垂直平分线上取若干点作为滑弧圆心，按上述方法分别计算，即可求得最小的安全系数。对于一级基坑（H＞15 m），K=1.43；二级基坑（8 m≤H≤15 m），K=1.30；三级基坑（H＜8 m），K=1.25。