引导学生善于运用可逆性原理解决问题,培养逆向思维的优良品质

二、引导学生善于运用可逆性原理解决问题,培养逆向思维的优良品质

有许多问题,可以巧妙地应用可逆性原理,如运动的可逆性、光路的可逆性、弹簧的可逆性、等量关系的可逆性、时间的反演性等。引导学生从反方向去分析,不仅可以使解题过程简捷,使问题化难为易,而且经过长期训练,培养了学生思维的灵活性、敏捷性和深刻性,提高了解题能力。

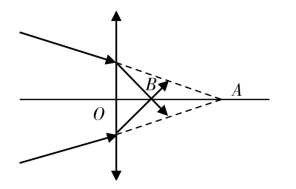
图4.3

例题2:如图4.3所示,一束会聚光束,不通过任何光学仪器时直接会聚于A点,若在A点之左侧距离为a的地方放一透镜,则会聚光线经透镜后会聚于B点,已知AB间距为b,求该透镜焦距。

分析:由光路图可知,所放透镜为凸透镜。沿着常规正向思维,此类问题的求解应当是先确定物距u和像距v,然后根据成像公式:1/u+1/v=1/f,来求f。但是,u、v各是多少呢?按光路的传播方向去寻找,似乎缺少条件,因而感到无从下手,思维受阻。如果把问题颠倒过来思考,根据光路的可逆性原理,设想在B点处放一点光源,则光线必沿原路返回。因此,使问题变为实物成虚像的情况。可把A点看成B的虚像,则有:

u=a－b,v=－a,代入得f=uv/(u+v)=[－(a－b)a]/(－b)=a(a－b)/b

在成像作图、确定光路等问题中也常常应用光路的可逆性原理,通过逆向思维而得解。