13.2.2  静子模型

13.2.2 静子模型

从单自由度的等效弹簧到完全的三维模型，定子模型是比较典型的，并且非转动部分可以用有限元库中的单元来描述。对于转子动力学，在定子部分也要引入阻尼。

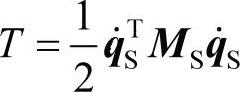
q_S的自由度向量描述了定子的位移域，惯性力由惯性坐标系下的动能离散方程来表达。

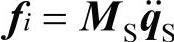
其中，M_S是定子质量矩阵，弹力来源于惯性坐标系中的应变能的离散方程：

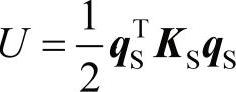
fe=K_Sq_S

其中，K_S是刚度矩阵。预加应力的二阶影响可以考虑进来。(https://www.daowen.com)

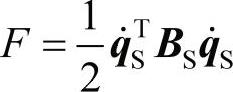
如果阻尼是黏性阻尼，则阻尼力源自于分散方程。粘性阻尼力有如下形式：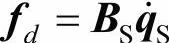

其中，B_S是粘性阻尼矩阵。

通常，静子组件中的阻尼和装配时的摩擦力有关。粘性模型就不适合了，滞后模型是比较适合的（见图13-6）。因为这个模型没有遵从因果关系，所以滞后阻尼的数学表述仅在频域有效。在时域里描述阻尼行为的一种方法是用可变的粘性阻尼。在这种情况下，粘性阻尼力可以写为：

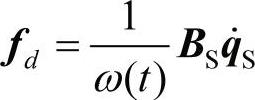
图13-6 静子粘性模型