15.2 简单两惯量系统
2026年01月14日
15.2 简单两惯量系统
如图15-2所示,在旋转机械应用领域最简单的模型是一个驱动设备和一个被驱动设备的两个惯量系统。
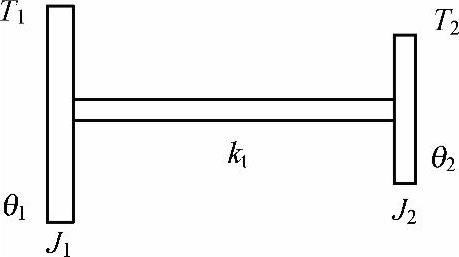
图15-2 两个惯量系统
θ1和θ2是惯量J1和惯量J2独立的转动坐标。两个惯量由弹性扭转刚度连接。两个惯量受两个外部扭矩T1和T2影响。运动方程可以由拉格朗日方程或者牛顿运动定律得到,写成矩阵形式为:
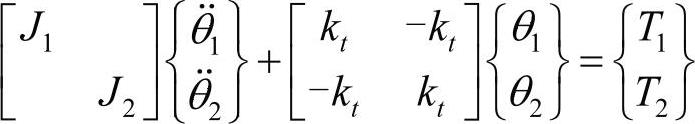
对自由转动(特征值)问题,假设谐波运动为:
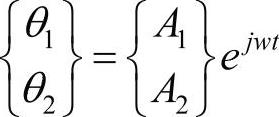
代入到控制方程中,得到:
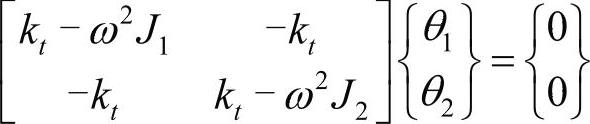 (https://www.daowen.com)
(https://www.daowen.com)
如果系数行列式为0,对任何A1和A2,上述方程都是满足的,这就是以下特征方程:
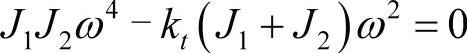
因此,得到系统的二阶固有频率和固有振型:
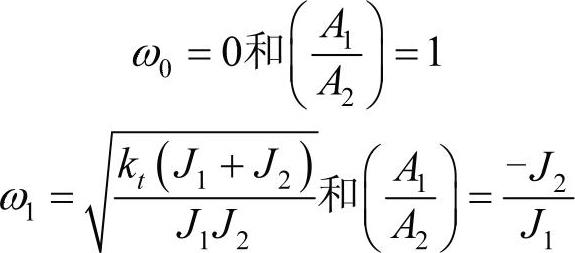
固有频率为0的模态被称为没有任何弹性变形的“刚体模态”,所有惯量以相同的幅值向同一个方向运动。在旋转机械领域,这个刚体模态是一个重要的特性,可以用来验证计算软件工具的准确性。在第1阶非0固有频率的弹性模态中,两个惯量向相反方向运动,轴上存在一个“节点”,仍然保持静止不动。图15-3为参数为J1=1kg·m2,J2=4 kg·m2和kt=2000Nm/rad的两个惯量系统的模态形状。
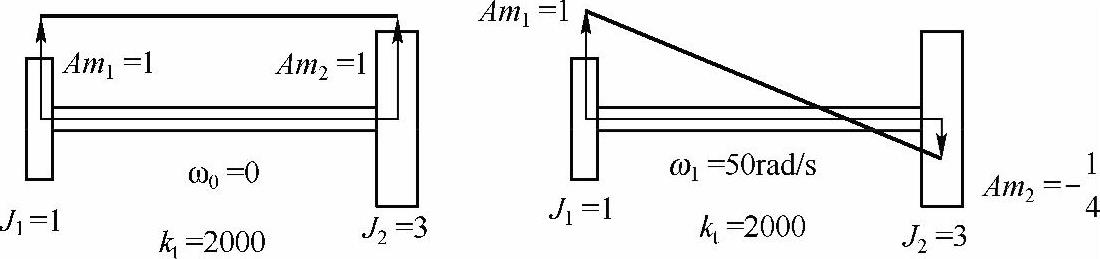
图15-3 两个惯量系统
