指向和无指向哲学的改变
像贝克莱一样,维特根斯坦在其《逻辑哲学论》中也论述了一种意义和无意义性的哲学,或曰有指向[sense]和无指向[nonsense]的哲学,它既有力又明确。一边是信息性经验陈述,另一边则是纯粹的胡言乱语,纯粹的废话;虽然纯粹的废话看起来也有可能像经验陈述。构成经验陈述的符号是一些已经被赋予了经验意义的词语:通过用法,它们每一个都与特定的可观察事物或事件相联系。另一方面,胡言乱语要么是不合语法的(例如“苏格拉底是同一的”),要么就是包括了我们“无法赋予任何意义”的词语。根据维特根斯坦的说法,哲学的唯一任务就是向那些谈论形而上学的人们“表明”,他们谈的都无指向。他这样总结其《逻辑哲学论》所传达的信息(6.53):“哲学的正确方法是这样的。不要说任何东西,除了能够说的——例如自然科学命题或与哲学不相关的那些东西:如果还有任何人想说些形而上学的东西,就立刻向他指明他没有赋予自己命题中的符号以任何意义。”
这就是我们所面对的挑战。但显然它还得加上下述观点才算完整:自然科学所使用的词语、符号或概念都可以通过经验定义——基于表述了直接经验的概念的定义——而加以定义。这是卡尔纳普在其《世界的逻辑结构》(1928年)中给自己定下的任务。他在此书中试图发展出一套科学术语的定义或“构造”的系统纲要:如果存在一条定义链将某一概念还原为直接经验术语,那么此概念就是“被构造的”。这当然就是一种从“数据”进行归纳的理论,只是应用对象是概念而非陈述。它坚守的这份纲领是不可能实现的。“概念的构造”和“理论的归纳”一样不可能。[18]
因此我们必须抛弃维特根斯坦那简单而直白的无意义或无指向的理论。它确实被抛弃了,而连同这种无意义或无指向哲学一起,实证论思想也开始分崩离析。(https://www.daowen.com)
许多人这些年来都在对之做一些小修小补。关于无意义性或胡言乱语的直白观念已经接连被各种更为复杂精微的观念取代了。[19]例如曾有人说,如果某个表达“不是科学语言中有意义的句子”,那么它就是“形而上学的”。(这种说法的意思是,好像所有形而上学家都分外注意他是不是在使用“科学语言”或某些人认为是“科学语言”的那种东西。)因此种种无意义性的命题都被冲淡了,直到有专家能识别它们的时候才得以重见天日。同样的情形也发生在形而上学观念之中。有一些言论在19世纪30年代时一直被认为是形而上学无指向的典型(因为它们既不是可证实的也不是可证伪的),然而现在大家都认为它们完全值得尊敬。而且所有这些思想上偷偷摸摸的改变都具有特设的性质,这是为了避免某种意义标准的非期望结果——这类标准无论再怎么修正都必然不充分。因为它必然同时过于狭窄也过于宽泛,这一点是显然的:它总是将期望的科学理论和非期望的形而上学理论错误地放在分界线的同一边。要知道,我们甚至可以依据人们提出的某些科学语言来“形式化”像理性神学那样的东西。[20]
这些人坚持的教条就是,意义[meaning](或现在所谓的“含义”[significance])标准必定等价于分界标准。然而我们为什么不放弃这个教条呢?试图挽救这个教条只能带来无穷的麻烦。我丝毫不认为这些麻烦值得认真对待。人们这样做难道是为了使神圣的实证论哲学免于被反驳?但它已经被反驳了,而且任何了解问题情境的人都已经通过各种方式放弃了它。因此我们为什么还要再为它而费心?
这些话就是我对分界问题讨论的总结。我已在《逻辑》中相当满意地处理了它在逻辑方面的大多数问题,特别是它和经验内容这个观念的关系问题,所以在此毋需赘述。
[1]根据某些流行的观点,维特根斯坦从未支持过意义的可证实性标准:人们说,他被石里克和魏斯曼(他表述过这种可证实性标准,见《知识》1,1930年,第228页及以下各页)误解和误读了。但这个观点是不对的,最好的证据就是石里克的论文,载《自然科学》[Die Naturwissenschaften]19,1931年,第145页及以下各页,特别参见第156页,石里克在那里说,自然律“可以依据进一步的经验而得到修正”,因此绝不可能被结论性地或绝对地证实。它也因而“不具备陈述的逻辑性质”:它不是陈述,而是(如果用赖尔那个来自于J.S.穆勒的理论中的术语来说的话)一种推理策略。石里克公开说过,他的理论得益于维特根斯坦给他的一封私人信件中的思想,而在发表此论文的相关文字时,他也无疑得到了维特根斯坦的一个词。这就表明至少在1931年的时候,维特根斯坦确实要求“真正的陈述”(echte Sätze)应该是那些那被“结论性地”或“绝对地”证实的陈述。如果读者不信,自可以检阅石里克在与维特根斯坦的讨论的直接影响下所撰写的,而且得到了维特根斯坦的首肯的那些著述,它们可以证明。(我还想补充说,在一次我和石里克的谈话中他自己也验证了这一点,当时他充满激情地为维特根斯坦的和自己的那些理论辩护并反对我的批判。而魏斯曼自己也承认了这个事实。)
[2]这两个纲领在很长一段时间都是维也纳小组特别是领军人物逻辑学家卡尔纳普的主导思想。见卡尔纳普《哲学中的伪问题》[Pseudo-problems in Philosophy](Scheinprobleme in der Philosophie);“通过语言逻辑分析颠覆形而上学”[The Overthrow(überwindung)of Metaphysics through the Logic Analysis of Language];以及《语言的逻辑句法》[The Logical Syntax of Language](特别参见第278页,那里断言了“逻辑分析表明”形而上学的伪[spurious]陈述“都是伪科学”)。他对此问题的兴趣还延伸到了“可检验性和意义”一文(在此书中我的可检验性分界标准被误解为某种意义标准)。据我所知,卡尔纳普讨论过一些糟糕的形而上学,但他从未通过他计划中的“逻辑分析”表明不可证实性或不可检验性都是因为(1)或(2)。但我将在本章表明,事实并非如此。
[3]冯·米泽斯的“公理”(它的公设如下:在事件或“集合”的任何概率序列中,某个特性P的相对出现频率都存在某种极限)可以写成一个全称-存在-全称-存在-全称陈述,如下:“对于所有概率序列,存在某个介于0和1之间的实数x,称为相对频率的极限,使得对于所有给定的任意小的分数y(满足y>0),存在某个自然数n,使得对于所有自然数n(满足n>ny),序列中特性P在至多n次事件中的出现次数m的相对频率m/n与x的偏差不大于它与y的偏差;换而言之,-y≤x-(m/n)≤+y。”
[4]〈对照拉卡托斯的《证明和反驳》[Proofs and Refutations],1976年。编者注〉
[5]注意到这两个数的和等于2+2x。令“P(x)”表示“x是一个素数”,同时令符号“(x)”表示“对于所有自然数x”,“(Ey)”表示“存在一个自然数y使得”,“&”表示“和”,那么我们可以将哥德巴赫猜想写成如下形式(注意到(x+y)和(2+x)
-y的和等于2+2x,即等于一个大于2的偶数):
(G) (x)(Ey)(P(x+y)&P((2+x)-y)).
这是此种形式表述中表示哥德巴赫猜想的最简形式。我们也可以定义(令“↔”表示“当且仅当”)自然数的一个特性Gdb(读作“具有哥德巴赫特性”),使得一个自然数x具有特性Gdb当且仅当2+2x是两个素数的和:
定义1 Gdb(x)↔(Ey)(P(x+y)&P((2+x)-y)).
根据这个谓词“Gdb”我们现在可以将哥德巴赫猜想表述为
(G') (x)Gdb(x)
或用语言表述为“所有自然数都具有哥德巴赫特性”。
[6]使用注3中的同样的符号,孪生素数猜想可以写成如下非常类似于(G)的形式:
(H) (x)(Ey)(P(x+y)&P((2+x)+y)).
这也是此种形式表述中表示孪生素数猜想的最简方式。我们也可以定义自然数的一个特性Etp(读作“被至少一对孪生素数超过”),使得一个自然数x具有特性Etp当且仅当它小于某一对孪生素数:
定义2 Etp(x)↔(Ey)(P(x+y)&P((2+x)+y)).
根据这个新谓词“Etp”我们现在可以将孪生素数猜想表述为
(G') (x)Etp(x)
或用语言表述为“所有自然数都被某一对孪生素数超过”。
顺带指出,我们可以给某一对孪生素数中的一个数——例如较小的数——指定特性“孪生素数性质的”或“Twp”;这就是说,我们可以定义
定义3 Twp(x)↔P(x)&P(2+x)
这将允许我们用下述定义代替定义2
定义2' Etp(x)↔(Ey)Twp(x+y)
[7]为了明确表示出这一点我们可以写出
(Hf) (x)(Etp(x)→(Twp(x)→(Ey)(Twp(y)&x<y<2x))).
(Hm) (x)(Etp(x))→(x)(Twp(x)→(Ey)(Twp(y)&x<y<2x)).
根据众所周知的逻辑原理((x)(A(x)→B(x)))→((x)A(x)→(x)B(x)),显然我们可以从(Hf)推导出(Hm)。同样显然的是,我们可以从(H)——即(x)Etp(x)——和(Hm)中得到(Hf);因此(H)和(Hf)的合取式,和(H)和(Hm)的合取式有着完全相同的力量。
[8]当然我们也可以构造出某种形式表述,使得(G)和(H)都能被翻译成此种形式表述,而且根据这种形式表述,它们的差别可以仅仅是逻辑形式上的差别。例如我们可以规定在符号“(Ex)”后面要注明一个下标,指出变量x的上界。于是(G)和(H)就可以表述为
(G') (x)(Ey)x-1(x>1→P(x+y)&P((2+x)-y)).
(H') (x)(Ey)(x>1→P(x+y)&P((2+x)+y)).
这样一来,它们之间的差别就可由如下事实表明:操作符“(Ex)”在(G)中是受约束的,而在(H)中则无;可以说这就造成了它们在逻辑形式上的差别;我们当然也可以将(H)视为无意义的而加以排除,这需要规定所有存在操作符都必须是受约束的(受不出现于操作符中的某些有限常数或某些术语约束)。但即使这样,我们也可以依据某种语言来完全充分地表达这两个猜想,而在此语言中它们的逻辑形式是等同的。
[9][*(1982年增补)有可能使(G)和(H)变得更类似。我们可以用符号|x|表示x的“绝对值”;因此|x|=x当且仅当x≥0,否则|x|=-x(因此是正的)。由此我们可以写出
(F) (x)(Ey)(P(|x|+|y|)&P(2+|x|+y)).
当我们令变量x和y在负整数中取值(即x,y<0)时上式陈述了(G);而当我们令变量x和y在正整数中取值(即x,y>0)时这个式子(F)又陈述了(H);而且它还陈述了
(I) (x)(Gdb(x)∨ Etp(x))
这时我们可以令x和y取遍所有正整数和负整数,除了0,也即x,y≠0。
有趣的是,虽然(I)的取值范围包括其他各式,但它却是(G)、(H)和(I)这三个猜想中最弱的。它甚至比(G)和(H)的析取式都弱得多。]
[10]在这里我假定,在给定b的前提下a的逻辑内容是在给定b的前提下a的概率的补数;也就是说,Ct(a,b)=1-p(a,b)。
[11]在冯·米泽斯的理论中,(HP)的否定确实与此前提相矛盾;因为在他的理论中,孪生正面朝上抛掷(之间仅隔一次抛掷)出现的概率是1/4,这蕴涵着这种情形的出现必定是比较频繁的。因此在其理论中,(HP)确实可以从“给定”的前提中得出,但在经典概率理论和测度理论的概率理论中它不从前提中得出(虽然它“几乎从前提中得出”)。(见下文第22节以下。)
[12]我们可以用某种标准符号语言来表明这一点。令“A”是完全可判定的谓词(例如“是红色的”、“具有哥德巴赫特性”或“具有非哥德巴赫特性的”等等),同时令“<”表示关系“被…超过”,我们定义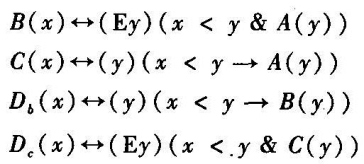
我认为这是产生此期望结果的最简定义了,当然也有许多其他的方式能达到同样的结果。
[13]〈这里的文字有缺损而且无法重构,丢失的几行文字包括一些进一步的例子。编者注〉
[14]我不知道某个表达式的“意义”是什么(而且我也不相信“‘是什么’问题”),但我假定某一(数学)定义至少能帮助我们去判定它。(https://www.daowen.com)
[15]〈对照费耶阿本德的“经验论问题”[Problems of Empiricism],载罗伯特·G.科洛尼[Robert G.Colodny]编:《超越确定性》[Beyond the Edge of Certainty],1965年,第164页。见波普尔的《逻辑》第38节注*3。编者注〉
[16]《逻辑》第25节末尾;另外参见《猜想与反驳》第118和388页。
[17]关于我的尝试,见我的论文“科学和形而上学之间的分界”,《猜想与反驳》第11章。见下一节注1到3。
[18]我在《逻辑》中指出了这一点(第25节末尾);其实我甚至在更早的时候——与维也纳小组的成员们进行讨论的时候——就指出它了。例如见我的论文“科学和形而上学之间的分界”(前引书)注释27以及注释25和27之间的文字。
[19]关于这些史实的更详细的介绍,见我的论文“科学和形而上学之间的分界”;见前一个注释。〈对照《无尽的探索》第16和17节。编者注〉
[20]见第25节注1,以及我的论文“科学和形而上学之间的分界”。我的论文之后卡尔纳普也写了一篇论文“科学概念的方法论性质”(见第11节注5和6以及第13节注12提到的参考指涉),在此文中他修正了一些被我的文章批判了的观点;特别是,他试图给出一种新的意义标准(现在被称为“含义标准”),并提供了两个证明,据他说,第一个能表明他的标准并非过于宽泛(第54-57页),而第二个能表明他的标准并非过于狭窄(第58-59页)。但其第二个证明中使用的某些假定表明,他的第一个证明是错误的,因此这个标准确实是过于宽泛;同样地,第一个证明中使用的某些假定表明,他的第二个证明是错误的,因此这个标准确实是过于狭窄。
