概率的归纳主义诠释
那么，什么是“归纳逻辑”？有两种观点：（ⅰ）概率计算的逻辑诠释，或曰“概率逻辑”，它与归纳无关；（ⅱ）概率计算的归纳主义诠释，它与逻辑无关——除非我们能以某种形式来表述它，使得在此情形中不出现任何概率逻辑。但这不是概率逻辑的推广，因为只要它是归纳的，它就会与逻辑诠释直接冲突；而如果我们认为它根本不出现，那么我们也就排除了任何形式的归纳论证。因此谈论归纳逻辑极具误导性。但是，如果概率计算通过诠释能产生出简单归纳规则，那么我们是否可以将之称为“归纳计算”，并将计算出来的概率称为“归纳概率”呢？
从形式上考虑，“归纳计算”就是加上了某个规则的概率计算，此规则断言了如下内容：
任何特性P的观察实例都将增加此特性P的概率（哪怕是极其轻微地增加）。因此，任何互补特性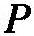
的观察实例都将减少P的概率（因为它将增加
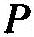的概率）。
卡尔纳普[14]称之为“实例相关定理”，他是这样论述的，“……特性的某一实例对预测具有同一特性的另一实例必定相关”。（他接着写道：“对于所有涉及预测未来事件的归纳推理，看来这都是一个基本特征。”）
举例言之，这个规则在实践中意味着观察到绿色的物体就增加了下一个物体为绿色的概率，或者观察到一个聪明的人就增加了下一个被观察到的人同样聪明的概率。正如卡尔纳普所表明的，它是称其为“简单归纳规则”的一种表现形式。
此处我不想讨论这个规则正确与否，也不想重开它是否有效的话题。现在我只想表明，即使我不用反例去证明，它也不是逻辑的组成部分，[15]这个规则本身的全部性质就使它不能被接受为概率逻辑的组成部分。
理由很简单，此规则的否定形式在逻辑上是全然成立的（并非“自相矛盾的”）。我指的是著名的赌徒谬误［gambler's fallacy］——等待大量的“正面朝上”序列段出现之后赌“反面朝上”，“因为翻盘的时候到了”。虽然就一般机会游戏而言我们知道这是一个谬误，但我们仍可以很容易地构造出一个序列（例如一个简化的正面朝上序列段），使得赌徒谬误能在此序列中产生成功的结果。
但上述归纳规则的数学形式表明了它的非逻辑性质，它不仅与赌徒谬误或“红或蓝”游戏相冲突，而且也与任何正常的随机序列相冲突。因为从客观上诠释，它预设了一种后效，而这在正常随机序列中是不会出现的。因此归纳规则与诸如以下估计相冲突——
它指的是抛掷一枚同质硬币而正面朝上的概率。
但上文所论的那个“收益递减定律”使我们看不到上述事实。这个定律确保简单归纳规则计算的概率趋于稳定，接近于随机序列“真的”或“客观的”概率值，并由此获得最终“成功”。然而，即便在如此这般稳定化之后，如果遇上一个不寻常的长序列段（不必纯粹），哪怕这个序列段从客观角度看在意料之内，归纳概率值依然会出现小范围的扰动。
所有形式的简单归纳规则都会与客观概率相冲突，即使是在日常的硬币抛掷游戏中也如此，我认为这一点值得再三强调。这个冲突一开始有可能很微弱，而且如果游戏序列无穷长，最终也会完全消失。但这改变不了下述事实：如果一位赌徒使用某种形式的简单归纳规则作为他的“生存指南”，或赌博系统，那么根据客观理论，涉及的赌注越高，可能的损失也必定越大。因为简单归纳规则计算出的概率总会一再偏离客观概率（在硬币抛掷游戏中我们认为这个客观概率是½）。一旦发生这种偏离，归纳赌徒就得接受从客观角度上看不利的赌注。虽然这并不必然导致损失，但（客观上）期望的或概然的损失却会高到任何我们能设想的地步：这明确指出了归纳概率不可能是重言的。
我相信上述讨论确立了两点：（ⅰ）这个（经过诠释的）归纳计算——即归纳概率——是不一致的[16]；（ⅱ）它的性质是非逻辑的。在休谟的《人性论》出版216年之后，我们确实没必要再去争论这后一点了，但看来人们显然仍未注意到休谟的相关论述。休谟的论证是这样：不可能存在有效的证明性（或逻辑性）论证，允许我们表明“我们未曾经验过的那些实例类似于我们已然经验过的那些实例”。因此，“即便已经观察了对象的频率或恒定合取，我们也没有任何理由推理得出超过我们已然经验过的对象的任何结论”。休谟写道，“要说经验”——经验告诉我们通常与某些特定对象相结合（合取）的那些对象仍会以此方式继续结合——“那么我会更改我的问题如下：我们为何能从这些经验中得出任何超过我们已然经验过的以往实例的结论？”[17]换言之，任何对归纳逻辑实践的证明都站不住脚，如果试图用经验为之证明，那就肯定会导致无穷后退。
因此卡尔纳普的规则确立的是具有同一特性的任意两个实例之间的相依性或相关性，这个规则是一个非分析的归纳原则；如果我们非要坚持它的话（而且要避免休谟的无穷后退的话），我们坚持的也不过是一个综合命题，也即先验有效的命题。
如果非要坚持它，我们又该如何论证支持它呢？无疑我们只能使用超越性论证：各种归纳逻辑学家都轻蔑地将康德称为先验论者和超越论者，但在这些逻辑学家中最流行的却也是超越性论证。（我非常敬仰康德，但我认为他最严重的错误就在于肯定地使用超越性论证来支持他认定是先验有效的那些原则。但在那个距离爱因斯坦还很遥远的时代，这种做法也是情有可原的。）[18]在罗素、杰弗里斯和赖兴巴赫的种种概率归纳理论中都能见到这种论证的身影。卡尔纳普也使用了它，但至少还带着某种迟疑和踌躇，在我看来这可算是一件令人赞赏的事情。他这样论述他选取函数m*的方法（这等同于选取简单归纳规则的特定形式）：
“上文的讨论表明下述论证尽管显然不是太强，但也可以支持m*。这两个m-函数都最简洁，本身也最自然，而其中m*是唯一一个并非完全不充分的。”[19]
若是选取另一个“完全不充分的”m-函数，就等于选取了我所谓逻辑概率。当然，它的“不充分性”包含着如下事实：它不蕴涵任何形式的简单归纳规则。但在我看来它必然如此，因为概率逻辑不是归纳的，因为归纳概率不是逻辑的，因为归纳逻辑是不可能存在的。
可是，尽管归纳逻辑不可能存在也确实不存在，但归纳逻辑学家却显然存在。实际上从培根以来（如果不是从亚里士多德以来的话）这些人遍地都是。要反驳他们并不容易，因为归纳概率——也即应用性的归纳微积分学——有可能是一致的，即便它们不是重言的。然而，仅当归纳概率明确地与逻辑概率和客观概率相区分时它们才是一致的。因为归纳概率的概率值一般情况下都不相容于逻辑概率和客观概率，甚至在像硬币抛掷这种对称的、独立的游戏中也是如此，这一点上文已有论述，更何况归纳逻辑学家们还常常用超越性论证来验证某些此类概率的正确性。[20]