补遗 关于意义分析的批判性评注
我不认为给验证度下定义是我们应该追求的目标，和大多数哲学家相反，我确信下述三个命题是真的。
（1）诸如“什么是正义？”或“什么是验证度？”此类的“是什么”问题永远都没有意义——没有什么哲学价值或科学价值；而所有针对“是什么”问题的解答，例如定义，也同样如此。必须承认，某些定义有时候也许能帮助我们回答其他一些问题，那些问题亟待我们解决，无法否定其存在：它们反映了科学或哲学中可能出现的一些真正困难。但诸如上述“是什么”的问题不可能有这样的困难。
（2）无论“是什么”问题的矛头指向何处——无论它是探求事物的本质还是事物的本性，无论它是探求某一表达的本质意义还是某一表达的正确用法，这些问题都没什么区别。根本而言这类“是什么”问题都是一样的。当然我得再次承认，对某种“是什么”问题的解答——例如指出人们常常混淆的两个词语在意义上的区别——可能并不是毫无意义，但前提是这些混淆带来了真正的困难。然而在此情形中，我们希望解决的不是“是什么”问题，而是由于我们依赖某些天真的直观概念所引起的特定矛盾。（下文讨论的第一个例子是关于导数的概念和整数的概念，这个例子就反映了此种情形。）我们的解答很可能是消除（而非澄清）那些天真的概念，并用另一个完全不同的概念取而代之。[41]另一方面，对本质主义问题（“是什么”问题）做回答完全无用。因为词语、概念或观点永远都只是工具，我们使用它们来表述自己的理论。（我非常坚定地反对关于科学理论的工具主义解释，但我在涉及词语、概念或观点时也是一个同样坚定的工具主义者。[42]）
因此，哲学（实际上也包括任何理性或批判性的行为）的主要目的不可能是澄清或定义观念、概念、观点或意义，或者是用更确切的术语去代替给定的观念、概念或意义。
（3）特别是用“确切的”术语去代替“不确切的”术语这个问题——例如用“确切的”或“精确的”术语来作定义的问题——是伪问题。它在本质上依赖于这两个不确切的、不精确的术语“确切”和“精确”。它的误导性不仅在于它强烈地暗示存在着并不存在的东西——绝对的确切性或精确性——而且也是过于情绪化的产物：它伪装成具有科学性和科学客观性，暗示说精确性和确切性是某种超越性的东西，是某种具有终极价值的东西，而使用不确切的术语就是错误的、非科学的或愚蠢的（不尽量使用流畅而简明的语言去表达倒的确是错误的）。然而并不存在什么“确切的”术语，“精确的定义”也无法使术语变得“精确”。定义总得在定义项中使用未经定义的术语（否则我们就将陷入无穷后退之中）；如果我们必须使用一定数量未经定义的术语，那我们是否打算使用些别的新术语是完全无关紧要的。当然，如果定义能有助于解决真正的问题，情形又大不相同；有些问题确实要依靠不断增进的精确性才能得以有效解决。实际上，这也是我们能合理地谈论精确性的唯一情形：对精确性的要求是空泛的，除非它与解决明确问题的要求有关。
在本节中我将为上述三个命题作辩护。
当代哲学——包括科学哲学——的主要潮流、趋势或思潮乃是将关于理论的工具主义解释和关于概念的本质主义诠释结合在一起；但我总觉得我这三个命题与之相悖。石里克对维特根斯坦某些观念的一段详述体见了这个趋向。石里克告诉我们，柏拉图对话中著名的“是什么”问题，例如《理想国》中“苏格拉底”提出“什么是正义？”这个问题，表明了苏格拉底哲学的主旨就是“我们所谓‘意义的探寻’。他试图厘清我们表述中的意义以及我们命题的真实含义……”石里克最后总结自己的立场道：“简而言之，我相信我们应当将科学定义为对真理的探寻，并将哲学定义为对意义的探寻。”[43]
石里克对哲学本质的定义仍然极具影响。我在本节开头给出的第一个和第二个命题明确表明了，我不认为这个定义能告诉我们什么有价值的东西（定义无法传递信息——对于那些需要一本字典的人除外），而且它也根本无法澄清大多数哲学家的任务或目的（如果他们愿意听的话，我将告诉他们：你们是真理的探索者）。顺便指出，我也不认为石里克正确地重述了历史上苏格拉底的观点。但我同意在柏拉图（和《理想国》中那位柏拉图化了的“苏格拉底”[44]）心中充斥着大量“是什么”问题。柏拉图主义和亚里士多德主义的形而上学确实产生了如下信念：哲学应当分析词语或概念的意义，哲学必须回答“是什么”问题，它也应当能给出定义。但这些观念仍然有着更深层次的根源：泛灵论。（这正是它为何难以连根拔除的意义之一。[45]）石里克的上述文字表明，作为柏拉图式唯心主义对手的唯名论者们和实证论者们都未能真正有效地批判这个信仰，而这个信仰现在又传承到了贝克莱、维特根斯坦及其追随者们身上——正如它传承到新亚里士多德主义中一般。受它的启发，埃德蒙·胡塞尔得出了“纯粹现象学”或“本质的直观”，G.E.摩尔［G.E.Moore］得出了“哲学分析”，而鲁道夫·卡尔纳普得出了“概念的阐明”。[46]无论这些学者身处思想流派之间的差别有多大，他们都认为哲学的任务就在于明确观念、概念或词语的意义。基于这个原因，我们可以将他们放在一块儿讨论。
我不打算重申我在其他地方对本质、意义分析和定义所做的讨论。[47]在这里我打算为我在本节开头提出的三个命题做辩护，我的方法就是分析一些prima facie［第一眼所见的］反例，也即一些被认为是对我这三个命题的反驳情形——人们认为在这些情形中定义澄清、阐明或确定了某些重要概念的意义，表明了定义的重要地位。我的第一个例子是将导数［derivative］（曲线斜率的导数或曰微商［differential quotient］或度量）定义为增量比［quotient of difference］的极限。我将略为详尽地讨论这个例子。我的第二个例子是罗素的“描述理论”［theory of description］——这属于此领域中的典型例子。我的第三个例子是维数［dimension］的集合论定义，第四个例子是塔尔斯基的真理定义。
我假定意义分析或阐明的信徒们认定这些例子能反驳我的三个命题。而我的目的在于表明，这些例子反而支持我的命题：它们不是关于澄清或“阐明”意义的例子，而是完全不同的东西——尝试解决种种具体问题，例如消除矛盾等等；而且它们达到目的（至少前两个例子是这样的）所采用的方法正是放弃澄清、确定或“阐明”有关概念的预期或直观意义。
我的第一个例子最具启发性。有人断言，数学基础问题的现代史大体上是一部对微积分的基础概念进行“澄清”的历史。通过将导数（曲线的斜率或函数增加率）概念定义为增量比的极限（给定某一可微分函数），这个概念也就变成了“确切的”或“精确的”；而我们也可以同样去“确切地定义”积分（曲线所围区域的面积或“求积”［quadrature］）的概念。这个例子对我们的问题而言有着关键的历史重要性。人们努力消除此领域中的矛盾，这种努力不仅构成了最近一百年甚至两百年来数学发展的主要推动力之一，而且也构成了当代探索各种科学的“基础”推动力，尤其构成了当代探寻“精确性”或“确切性”的推动力。伯特兰·罗素在谈到这一发展过程中最重要的阶段时写道：“因此，当维尔施特拉斯［Weierstrass］及其追随者们向数学家表明，他们最为珍视的命题一般而言都是假的时候，后者才从他们的‘教条主义迷梦’中醒了过来。麦考利［Macaulay］比较了数学的确定性和哲学的不确定性后这样问道：谁曾听说过有人会反对泰勒［Taylor］定理？如果他现在仍然活着，他自己就会听到这样的反对声，因为它正是为现代数学思考所推翻的定理之一。数学信念的这种大地震已经导致了人们对形式主义的喜爱，因为在那些忽略其动机的人看来，形式主义最糟糕的地方也不过是令人愤慨的墨守成规而已。”[48]
在阅读这段引文的时候，人们往往会误解罗素的意思，以为他也认同下述观点——我相信此观点是正确的：如果没有“这种大地震”，也即没有除去矛盾的迫切需要，那么对形式主义的喜爱确实“也不过是令人愤慨的墨守成规而已”。但我认为罗素实际上是想表达如下观点：如果没有什么迫切的需要，没有什么迫切需要解决的问题，那么仅仅要求精确性是不合理的。
但这些都很次要，我的主要观点是这样的。包括数学家在内的许多人都认为，依据序列的极限来定义导数，就相当于以这种定义方式来分析、确定或“阐明”导数这个被定义项的直观意义。但这个流行的观点是错误的。
“定义”这个词的意义有许多种，我们可以通过下面关于数字23的一些可能的定义来考察其中的两种。
我们可以写出：
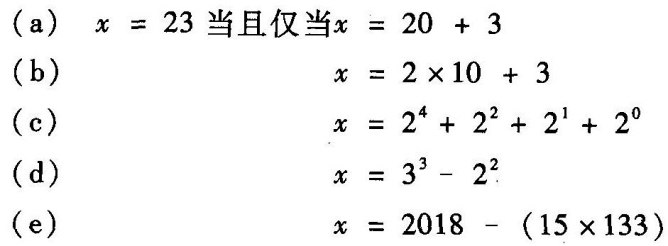
大多数人会说，等式（a）和（b）能定义“23”，而如果我们想要一个基于2的幂的定义的话，（c）也算；但（d）和（e）都不是“23”的“合理定义”，即便它们当然都是具有真值的等式，因为它们无法分析、阐释或阐明“23”的意义。没有哪个理解“23”意义的人能依据（d）或（e）说明或“阐明”其意义。
而我的观点是这样的。在当前被大多数学家和逻辑学家所认可的“定义”的一般意义上，（d）和（e）都是完全合法的定义；[49]而且，在导数被定义为增量比的极限的“定义”这个词的意义上——我总觉得意义被处理问题的通常方法给遮蔽住了——（d）和（e）同样是足够好的定义。
牛顿、莱布尼茨及其后继者们都不否认可以用特定序列的极限计算导数或积分——粗略而言，正是在这个意义上我们也可以用（d）或（e）来计算x。但他们都不认为这些极限就是可取的定义，因为它们不能赋予导数或积分以观念以意义。[50]
因为导数是对速度或曲线斜率的度量。某一物体在特定时刻的速度是真实的——它是物体在此时刻的一个具体（关系性）属性。但与此相反，平均速度序列的极限则是某种高度抽象的东西——某种仅仅存在于我们思想中的东西。平均速度本身就不真实，它们的无尽序列就更不真实了，而这个无尽序列的极限又是超出上述不真实存在物的纯粹数学构造。从直观上讲我们有相当明显的理由认为这个极限必定在数值上与速度相吻合，而且，如果这个极限可以计算出来，那么我们就可以通过它来计算速度。但是根据牛顿及其同时代人的看法，如果我们将速度定义为等同于这个极限，那我们就本末倒置了。相反，我们应当将速度定义为物体在某一特定时刻或在轨迹上某一点的某种真实状态，而我们可以依据我们能够想到的任何数学工具来计算它。
至于曲线在给定某一点上的斜率，情形也是如此。此斜率的度量等于曲线其他段上平均斜率（而非实际斜率）度量序列的极限。但就其正确意义或本质而言，斜率并不是序列的极限：有时我们确实能用尺规将其画在纸上，而极限在本质上是抽象的，在实践中很少接触到或认识到，只能用数字序列不断逼近它。
同样，我们也可以用内切多边形序列逼近圆，可以近似地（近似到任何期望的程度）用这种方式计算其面积或“求积”）；但就其意义或本质观点而言，说什么“圆是这个内切多边形序列的（未实现的）极限”，那是毫无意义的。因为正是圆定义了这个序列，即将之定义为内切于圆的多边形序列，而不是序列定义了圆。同样，虽然圆的面积明显等于这个内切多边形面积的极限；但用这种方式来阐明它是毫无意义的，正如我把我的猫的体积（考虑它当前的体形）描述为内切多面体的极限毫无意义一样。我的猫就是它自己，正因为猫就在那儿，猫自身是存在的，我才能谈论什么内切多面体，并认识到它们能不断接近于猫的形状；在此情形中，它们的体积也就显然接近于猫的体积了。因此我可以用这个抽象的多面体序列来进行计算，但是，由于这个序列被定义为内切于我的猫，所以在“定义”的旧意义上我们不能用这个抽象序列来定义猫的形状或猫的体积。
贝克莱是这样谈论这个问题的：“……无论这些有助于应用现代求积法的类比或表达多么方便，我们也还是未能对流数［fluxions］原初的真实本质有一星半点的了解；只有了解这种本质，我们才能依据它来形成流数这个观念本身。”[51]根据他的意思，纯粹为了计算方便的种种方法不可能成为阐明或定义。
这也是当时所有数学家认同的观点，其中包括牛顿和莱布尼茨。
如果从现代观点来看，我们会发现我们已完全抛弃了微积分的创始者们以及贝克莱等人所持有的那种关于定义的看法。我们已经放弃了那种认为定义解释意义（例如导数的例子中所表明的）的观念。许多人没有认识到这一点，那是因为我们仍然在使用“定义”这个古老的词语来表达一些等式，但我们用这些等式的目的乃在于消除导数的概念或本质，而非打算说明它；另一方面，这也是因为我们仍然保留着“微商”或“导数”这样的术语以及dy/dx这个旧有的符号，但这个符号曾经表示过的意义已经被我们否弃了。这些术语、符号现在的唯一功用就是作为被定义项——序列的极限——的名称而已。
因此我们已经放弃了“阐明”这个糟糕的任务，我们发现这个直观的观念将产生矛盾。不用它我们也能解决问题，同时保留最初以这个直觉观念为基础的大量计算技术。更精确地说，我们仅仅保留这些技术，只要它们是可靠的，并同时依据这些技术来消除这个观念。导数和积分都可以被消除；取代它们的，实际上是一些计算极限的标准方法。
但这场改变是暗中进行的，对旁观者（特别是本质主义旁观者）而言多少还有点不可理解，因为应用于导数的旧术语“定义”以及旧的名称符号都依然保留着。这种保留是适当的，只有本质主义者会对此提出异议。
有趣的是，这整个辉煌的发展本来可能被压制在萌芽状态之中（即阿基米德［Archimedes］的时代），幸好那个时代的数学家们对于贝克莱的下述主张并不太敏感；这个主张本身倒是合理的，它认为，我们应当严格遵循逻辑规则，而且应当永远只谈论有意义的东西。
贝克莱在《分析者》中谴责了牛顿以及那些“外国数学家们”（例如莱布尼茨），因为他们用不合法的推理得出了他们的数学结果，即流数理论或曰“calculus differentialis”［差分法］；现在我们知道，贝克莱的这个指责是正确的。当他指出这些人所用的符号没有意义时，他也是完全正确的。他写道：“没有比这更容易的事情了：为流数和无穷小发明一套表达式和记号，将一阶、二阶、三阶、四阶和更高阶导数记为x、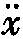
、
、
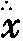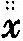等等。这些表达式确实明晰而独特，而且很容易就能让我们相信，这样的数学创造能继续下去，不用担心有什么阻碍或边界。但是如果……我们能更深入地思考，如果我们暂时将这些表达式放在一边，想一想那些被假定是可以如此这般通过符号来表述或标示的事物本身，我们就会发现大量空洞无物、晦涩不清和混淆迷茫……以及显而易见的不可能和矛盾。”[52]
但同时代的数学家们并不听从贝克莱的劝告。他们得到了成果，也不惧怕什么矛盾——只要他们认为能够用一些小技巧来避开这些矛盾。幸好历史是这样发展的，因为我们都知道，企图去“分析意义”或“阐明”其概念都将一无所获。贝克莱的下述观点是正确的：在他的意义和“意义”这个词语的传统意义上，所有这些概念都是无意义的——它们都是空无，因为它们不指称任何东西，也不代表任何东西。如果那时候的人们意识到了这一点的话，微积分的发展将会再次停滞下来，正如它曾经停滞过一样。让微积分得以辉煌发展的，正是对精确性的否定，正是对所有意义分析或阐明的最本能的否定。
这整个发展过程下隐藏的问题就是，人们保留下了强有力的微积分计算工具，却不去触及早已在它身上发现的那些矛盾。无疑我们当前的方法要比早期的方法更确切。但这不是因为它们使用了“确切定义了的”术语，也不意味着它们本身是确切的：包含极限术语定义的要点就在于它永远是一个存在断言，而“存在着数”这句简短表达的意义，已经成为当代数学大混乱的核心。无论我们如何看待连续统理论问题或布劳威尔的直觉主义，毫无疑问，只有当布劳威尔为我们展示构造性证明和非构造性证明之间的差别——今天甚至其对手也承认了此差别的意义——我们才从自己教条主义的迷梦中惊醒过来。[53]这件事也有力地支持着我的观点：确切性不是绝对的，使用“确切”或“精确”这样的术语，并认为它们本身也有某种程度的确切或精确的意义，都是不确切的，也是高度误导性的。
我的第二个关于定义或阐明的例子是罗素著名的“描述理论”。它理所当然的任务就是去定义或阐明像“这个、那个、如此这般”这样的短语（例如“那个大于19的最小的素数”）的意义。但还有其他一些问题也要求我们去定义这样的短语。罗素说其中一个问题是他非常不满迈农［Meinong］关于非存在实体的存在模式的观点。[54]另一个问题更重要一些，它表明了我们可以从不包含“如此这般”这类表述的陈述中，逻辑地演绎出包含这类表述的陈述；例如我们可以从“23是一个素数，而且在19和23之间不存在任何素数，而且19＜23”中演绎出“23是那个大于19的最小素数”。
罗素对此问题的回答，其基础当然是去分析包含着短语“如此这般”的陈述的直观意义。但他得出的定义却恰如导数定义的情形一般，成了否弃或消除直观被定义项的方法。符号被保留下来，但已经变成了适用于定义项的速记符号而已。因此，“定义项是否能正确地传达出符号本来的意义”这个问题也失去了价值：被定义符号的意义仅仅在于成为适用于定义项的速记符号。
正因为如此，讨论罗素定义的大多数批评（在这里我指的是G.E.摩尔在P.A.希尔普编辑的《伯特兰·罗素的哲学》一书中发表的文章）也都失去了意义，虽然这些批判者可能比罗素更敏锐地注意到了被分析术语的直观意义。
第三个例子要说的是维数的定义（由庞加莱、布劳威尔、乌雷松和门格尔［Menger］发展而来），我在《逻辑》中对此也有所涉及。[55]康托尔［Cantor］（于1878年）证明了一维连续统的点的基数等于一维以上的连续统的点的基数，从此之后，维数的拓扑不变性问题就日益急迫了，而上述定义的主要作用就在于能帮助我们解决此问题。当然，以集合论术语［set-theoretic term］表达的维的定义也能解决许多其他问题。若考虑此定义意欲解决的问题类型的话，这个定义中最引入注目的地方在于，定义项采用了集合论术语。要注意，我说的是“集合论术语”而不是“确切的术语”。实际上，这个定义所依据的直观集合论的确切性是比较令人生疑的，且同时还存在着另一个更确切的（公理化的）集合论。但现实情况却是这样——导致了更为确切的理论发展的那些问题，与这个定义意图解决的特定问题毫不相干；此外，公理化集合论的种种不同形式也可以不加更改地接纳和采用这个定义。
我的最后一个例子是塔尔斯基关于真理概念的定义。塔尔斯基说，当时他的唯一目标就是在真理的绝对意义上给真理下定义；更精确地说，在“符合事实”或“符合实在”的意义上去定义谓词“是真的”。但显然，这个目标超出了我们解决某些非常严肃的问题的需要。
一方面，真理的观念看上去有着极为重要的功能。例如哲学家们就希望能说“探求真的理论并不同于探求有用的工具”。而逻辑学究也希望能说“如果某一有效推理的结论是假的，那么前提就不可能是真的”。换言之，真理这样的概念是我们的真实需要。
另一方面，人们常常断言，短语“这是真的”——例如“3+5=8这是真的”——永远都是逻辑上冗余的，因为“3+5=8”也陈述了完全一样的内容。这样的断言是完全正确的。另外，人们也常常指出（这就不那么正确了）像“‘3+5=8’是真的”这个表达中的“是真的”也是冗余的。（我说“不那么正确”，这是因为这个表达是“这个陈述‘3+5=8’是真的”的缩写；而在这里“是真的”显然不是冗余。）人们不仅认为真理的概念是一种冗余，而且还指出真理的概念产生了像说谎者悖论那样的悖论。最后人们指出，从直观上看，“与事实或实在相符合”这个概念同时也是晦涩不清的，而且它无法避免这种性质，也没有什么希望能让它摆脱这种性质——因为当我们谈论事实或实在的时候，我们想意味什么呢？而当我们谈论陈述或命题与事实相符合的时候，我们又想意味什么呢？维特根斯坦曾在《逻辑哲学论》中说过，这种符合就是结构上的类似——就像某段旋律和电唱机针头跳动之间的符合一样。但他这种错误观点只能增加其晦涩的性质而已。
粗略来说，这就是我们当前的问题情境，或者说问题情境的一部分；而塔尔斯基以最直接的方式取得了成功，他扫除了这里提及的所有问题和晦涩之处。我们必须用这种成功来判断其成就。此外，他的理论还在更加技术化的数理逻辑领域、甚至是在数学领域中取得了令人震惊的丰硕成果。
对于日常生活中直观的真理概念，塔尔斯基的工作也提供了不少有价值的意义分析。但他不是给出了真理概念的定义，相反，他表明如果我们不加任何谨慎思考就将真理定义引入日常语言之中的话（即那种在我们能用它来谈论任何事物的意义上具有“普遍性”的语言），这种语言将变成不一致的。那么在这个意义上，对真理的直观观念的“确切”定义也就变得不可能了。但是，如果我们对塔尔斯基的工作稍加借鉴，便仍然可以在日常语言中相当一致地使用真理概念。需要借鉴之处简而言之是这样的。[56]我们必须在使用的语言和涉及的语言之间作出区分；也就是说，区分在使用中的语言和被谈论到的那部分语言；我们也必须明确，如果我们对某一陈述作出断言说它是真的，那么这个陈述属于涉及的语言，它与在使用中的语言不同——也即与我们断言此陈述为真时所使用的语言不同。当然，这里所能借鉴的绝不是什么“精确的定义”。
塔尔斯基表明，只有对那种被诠释的形式化语言——人工语言系统，我们才能给出精确的定义。（最为重要的一点是，“合式公式”［well formed formula］的精确定义必须先于“真的陈述”的定义。）借助人工形式化语言，塔尔斯基给出了定义真理的方法，而不是定义本身；他的理论的重要性在于下述三点：第一，表明了如何针对此类语言去定义真理；第二，表明了可以给出此类定义；第三，表明了可以依据这个定义来得出结论。内嵌于塔尔斯基理论中的这些要点远远比他实际能给出的定义要重要得多，在某些特定的非常简单的语言实例中，这些要点勾勒出了塔尔斯基所用的方法。[57]
我还可以给出许多例子，但上面这四个例子，加上我自己对验证度的定义，已经能够明确阐述我的主要论点了：定义、“分析”或“阐明”问题本身没有意义，只有在与其他更严肃的问题联系起来之后它们才有意义。用某一更“确切的”术语来代替当前的术语，这绝不可能是什么理性的行为——实际上这并不是严肃的问题。但是，如果它与某些严肃的问题相关联，而这些问题又将因为使用定义或澄清术语变得更易解决，那么它就有可能变成一项严肃的任务。[58]
我很乐于承认，精确性的增加也非常重要：这不是因为它本身的缘故，而是因为它能增加理论的可检验性。（对照《逻辑》第37节。）在其他一些情形中，它也能帮助我们辨别术语间的分歧，这也是解决严肃问题过程中的需求之一。但我们绝不能把精确性供奉为偶像，也不能像对待明晰性或易懂性那样，认为它本身就具有价值。
顺带指出，有一大类问题，看上去似乎需要定义才能得出进一步的解答，但实际上定义所做的仅仅是将实际问题转变为言词问题，从而剥夺了它们的经验性质。例如，假设我们希望能解决以下这个虽然非常含糊但又可能很实际的问题：“所有艺术作品都是美的吗？还是有些艺术作品不美？”有些人会试图定义“艺术作品”或“美”等等，而不是去想一想那些可以合理地被描述为既是艺术作品而又不美的东西；对于这种做法，我们应该保持警惕。换言之，我们应当寻找例子。勋伯格［Schönberg］的《月光下的彼埃罗》［Pierrot Lunaire］、奥威尔［Orwell］的《1984》、某些讽刺画（例如莱奥纳尔多·达·芬奇［Leonardo da Vinci］的）和大人国中的格列佛［Gulliver in Brobdingnag］都可能是合格的例子。这个例子当然是我主观概述的，它所得出的答案当然也颇为可疑。但我们可以改进它。另外，答案的含糊和可疑恰好印证了问题的含糊和可疑。另一方面，如果我们将“艺术作品”定义为其特性包含着美的东西，那么我们就可以稳妥地带着“精确性”来回答我们的问题了。但这样做的时候我们就（很可能是不明智地）用某个纯粹言词问题代替了我们的实际问题，对实际的艺术作品所做的思考也不会再对问题的解决有任何贡献了。我刚列举的作品名单也不再是主观的概述，而将变得完全不相关了。我们可以先验地指出，这张名单中的每一件作品要么是美的（这与我原先的认识相反），要么就不是艺术作品（也与我原先的认识相反）。而且，即便我们不了解这份名单或其他类似名单所提及的任何艺术作品，我们也可以作出此类断言。（在科学领域中也有非常类似的从实际问题到纯粹言词问题的转变，这就是约定论所作出的“丰功伟绩”，也是所有约定论诠释或约定论策略所作出的“丰功伟绩”；对照《逻辑》第19和20节。而在哲学中，哲学问题或其他问题向言词问题的转变——特别是从定义和“阐明”公然变成“分析”哲学的目的开始——就根本是一场祸害了。）
整部科学史所给予我们的一个重要教训，可以借由我这些例子强调出来：绝对确切性是不存在的，甚至在逻辑学和数学中也不存在（仍在继续的微积分历史就表明了这一点）；我们应当控制确切性，使它不超出解决手头问题所需要的程度；而针对“更确切的东西”的需求本身就不可能构成真正的问题（当然，例外就是如果它在增进确切性的同时也能增进理论的可检验性）。
为了意义分析而意义分析，永远是无价值的。当某一词语的两种或多种意义被习惯性地混淆时（例如“概率”的例子所表明的），我们最好注意到这些意义之间的区别。有些陈述在这个意义上真，有些陈述在那个意义上真，但不能同时与两个意义都相容。除此之外，像“什么是验证？”或“‘验证’是什么意思？”这类问题都是空洞的。[59]
[1]在《逻辑》中（附录*ⅳ）我给出了一些用于形式概率计算（它的一种解释就是逻辑解释）的公理系统。虽然读者毋需熟悉这些数学技术，为了说明的完整性，我仍打算在这里陈述这些最简公理系统之一。它只包括三个公理，第一个引入了概念p（a，b），第二个引入了积的概念ab（读作“a和b”），而第三个引入了补集概念ā（读作“非a”）。
A 至少存在两个元素a和b，使得
B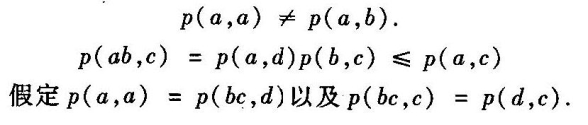 
C p（ā，b）=p（c，c）-p（a，b）
假定对于某个元素d有p（d，d）≠p（d，b）
对此我们还要增加一个公设，引入两个元素a和b的（替代性）恒等a=b：
（*）a=b当且仅当对于所有元素c有p（a，c）=p（b，c）。（在此情形中，a和b在任何地方都可以相互替代。）
通过采取基于a=b的定义规则，我们可以增加进一步的定义；例如我们可以照例定义“a∨b”（读作“a或b”）如下：
a∨b=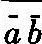
这个简单的公理系统允许我们不借助任何布尔代数定律而演绎出许多众所周知的概率计算定律，例如自反律
（1）和B的直接结果就是非常重要的单调律
和一般乘法律
这个系统的一个较远的结果是一般加法律
此外我们还能得到一些在通常计算中得不到的定理，例如：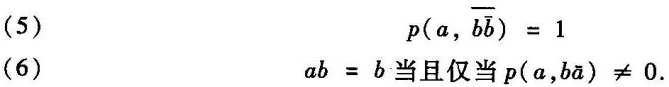
在这种逻辑诠释中，等式“a=b”应读作“逻辑等价于”（或“可互相演绎”），而“ab=b”应读作“从b推导出a”，这也可以写成“a≥b”或“b≤a”。
[2]〈见R.C.杰弗里［R.C.Jeffrey］《判定的逻辑》［The Logic of Decision］，1965年，第11章。——编者注〉
[3]〈对照唐纳德·T.坎贝尔：“进化的认识论”，载P.A.希尔普编：《卡尔·波普尔的哲学》，第413-463页。编者注〉
[4]疑原文有误，应为“这才可以使得p（h，e）尽量大”。
[5]致康林［Conring］的信，1678年3月19日；见格哈特［Gerhart］编辑的《G.W.莱布尼茨哲学论文集》［Die philosophischen Schriften von G.W.Leibniz］，1875-1890年，第ⅰ卷，第195页及下页，以及路易·库蒂拉［Louis Couturat］的《莱布尼茨的逻辑》［La Logique de Leibniz］，1901年，第268页。
[6]休谟将论证分为“证明［demonstration］、证实［proof］和概率”，虽在《人性论》区分不那么明确，但在《人类理解研究》中有详细论述（参照第ⅵ节第一个脚注）。
[7]在卡尔纳普的“可检验性和意义”一文中（《英国科学哲学杂志》3，1936年，第427页）可以找到他的这个翻译，那里他也提及了《探究》。一两年之后我向他建议说“验证度”可能是个更好的翻译，但因为他不赞同，我也就接受了他的翻译。（术语“验证度”是我的朋友休·N.帕顿［Hugh N.Parton］教授给我的建议。）
[8]《符号逻辑学杂志》20，1955年，第304页（粗体为原文所有）。开米尼的回复应做如下修正（见第304页从第16行到页底）：“y给予x的支持的度量”应改为“x对于y的说明力的度量”。
[9]对照《英国科学哲学杂志》12，1945年，第99页注2。
[10]〈参见亚科·欣蒂卡［Jaakko Hintikka］：“通过枚举进行归纳和通过消除进行归纳”［Induction by Enumeration and Induction by Elimination］，见I.拉卡托斯编：《归纳逻辑问题》［The Problem of Inductive Logic］，1968年，第192-216页。编者注〉
[11]我在《逻辑》第82节倒数第二段之前的最后一句话中对此观点做了简要的陈述。为了使这个观点成立，我们就必须使验证度的定义满足下述要求：验证度不仅应当相对于以检验的形式出现的证据，而且应当相对于其他理论。我用所谓的验证度的“相对化形式”做到了这一点；见下文第32节。
[12]C.G.亨佩尔［C.G.Hempel］坚持的是一种实例主义的［instantiationist］确证理论，但非常奇怪的是他也坚持如下理论：如果两个假说h1和h2不一致，那么不存在任何证据e能同时确证这两个假说。参见《逻辑》附录*ⅶ注13。
[13]非常有趣的是，从历史而言直至1600年时“实例”本身指的都是“反例”或“相反的实例”（词源是instantia，即某种障碍：在此情形中，就是横在认可和接受之路上的障碍）。
[14]〈关于这里引入的概念“背景知识”，波普尔最初发表于1954和1957年。见《逻辑》第401和404页。编者注〉
[15]对于这些史实，见B.A.谷德［B.A.Gould］，《发现海王星的历史：向史密森研究所呈交的报告》［Report to the Smithsonian Institute on the History of the Discovery of Neptune］，1850年。
[16]例如“可以从hb中推出e”可以用概率语言重新写成下述形式
p（e，hbe）=1
从这个形式就可以立刻得到较弱的公式（a）。见《逻辑》附录*ⅴ第356页公式（+），以及此公式后面的讨论。
[17]原文有误，此处（e）应为（f）。
[18]在《逻辑》附录*ⅳ和*ⅴ中给出了下述公式B1和B2：
p（e，b）≥p（eh，b）=p（e，hb）p（h，b）
在给定这两个公式的前提下就可以从（aa）和（bb）中推出（cc）。
[19]见《逻辑》附录*ⅸ第一篇札记中公式9.2和10.1（第400-401页）。当前的定义D是注*2的（10.1*）。
[20]这个定理也适用菲舍尔［Fisher］意义上的“h的似然性”l（h，e），它的定义是
l（h，e）=p（e，h）
虽然它是概率，但不是h的概率。
[21]“虽然逻辑有可能……建立某种标准以判定某一陈述是不是可检验的，但至于人们是否已经竭尽全力去检验这个陈述，这个问题逻辑是无法作出回答的。”（参见《逻辑》第11节第54页。）
[22]〈这里的文字有缺损而且无法重构。编者注〉
[23]见《逻辑》附录*ⅸ，那里重印了我的三篇论述“确证度”的论文。（《英国科学哲学杂志》5，1954年，第143页及以下各页。参见5中的更正，第334和349页；6，1955年，第157页及以下各页；7，1956年，第244页及以页，第249页及以下各页，以及第350页及以下各页。）要注意，在这些文章中我使用的是术语“确证”而非“验证”，而且我在表示x的内容时用的是符号“C（x）”而非这里使用的“Ct（x）”。在这三篇论文的第一篇中有几条“预设条件”是我在这里没有提及的。参见附录*ⅱ和附录*ⅳ。〈参见《猜想与反驳》的补遗。编者注〉
〔原书中缺失本节脚注1在正文中的标注位置，译者自行斟酌，将之标注于此处。〕
[24]［*写下此段的时候我还不知道，J.冯·索德纳［J.von Soldner］早在1801年就计算出了光粒子擦过太阳边缘时的弯曲。这个事实是斯坦利·L.亚基［Stanley L.Jaki］在其杰出的论文中提到的，载《物理学基础》［Foundation of Physics］8，1978年，第927页及以下各页。］
[25]对照《逻辑》第81节注1，那里提及雅妮娜·霍西亚松-林登鲍姆［Janina Hosiasson-Lindenbaum］。
[26]原文有误，应为ab。
[27]如果我们采用下述做法的话，那么我们并不用要求一致性——在分子和分母中加入一个“-p（ā，a）”，将上式写成如下的更复杂的形式C（a，b）=p（b，a）-p（ā，a）-p（b）/（p（b，a）-p（ā，a）-p（ab）+p（b））。这样一来，如果a是不一致的，我们就能得到C（a，b）=-1。类似这样的方法也能适用于相对化定义（ⅷ）。
[28]这等于假设了Ct（a）的相对化：我们可以写出
Ct（a，c）=C（a，a，c）=1-p（a，c）
[29]见注4。
[30]见注4。
[31]参见《逻辑》附录*ⅶ。卡尔纳普也得出结论说，（如果确证度被定义为概率，那么）所有全称定律的概率都为零，因此它们的确证度也都为零；见其《概率的逻辑基础》，1950年，第570页及下页。因此在卡尔纳普的理论中全称定律都是不可确证的。基于这个原因，卡尔纳普（我也一样）在碰到全称定律的时候就放弃了概率或确证度，转而采用另一个新概念——虽然他这么做仅仅是特设地。他将这个新函项称为“资格实例确证”，但我已在《英国科学哲学杂志》（7，1956年，第252页及下页）中指出了其中所产生的矛盾。实际上，根据卡尔纳普的著作第573页公式（17），对于两个仅仅在语言表述上有差别的定律而言，证据一样，但得出的“资格实例确证度”竟然彼此大不相同。
[32]如果a是全称项，同时p（b）＞0，那么p（a，b）-p（a）等于零；这个值得我们注意的事实与卡尔纳普的概念“被确证的”有着极大关联（《概率的逻辑基础》，第463页及下页）。之所以这么说，是因为卡尔纳普在定义“b对a的确证”Co（a，b）时候，依据的表达式等价于（以本书所用的符号来记）“p（a，b）-p（a）＞0”；也即等价于“p（a，b）＞p（a）”。这样一来，如果对于全称定律有p（a）=0（在卡尔纳普的理论中确实如此），那么就不存在任何证据陈述b能“确证”全称定律a。在卡尔纳普的意义上，因此定律无法被“确证”。此外，Co与卡尔纳普的确证度概念相矛盾，因为这个概念是一种概率（可以记为p（a，b）），这一点可以从下述两个重言式中看出来：其一是“如果x不是暖的而y是暖的，那么下述情形永远不会发生——x比y更暖或者和y一样暖”；其二是（这是更为直接的表述）“如果z没有确证x而z确证了y，那么下述情形永远不会发生——z对x的确证程度比z对y的确证程度要好，或者z对x的确证程度和z对y的确证程度一样好”。由于这也可以表述为“如果非Co（x，z）而且Co（y，z），那么非p（x，z）≥p（y，z）”，通过用Co所依据的等价表达式进行替换我们就有：
（1） 如果p（x，z）≤p（x）而且p（y，z）＞p（y），那么p（x，z）＜p（y，z）
（2） 如果p（x，z）=p（x）而且p（y，z）＞p（y），那么p（x，z）＜p（y，z）（根据（1）式）
（3） 如果p（x，z）=p（x）而且p（y，z）＞p（y），那么p（x）＜p（y，z）（根据（2）式）
但这是荒谬的：我们可以选取任意接近1或等于1的p（x），那么如果我们再选择p（y，z）等于1/2，p（y）等于1/4，这样一来上式就不成立了；或者更一般地，我们也可以选择y=xz，而且假定x和z是独立的。（见《英国科学哲学杂志》7，1956年，第254页及下页；参见我的《逻辑》附录*ⅸ的导论性评注。）
[33]我们应当记得在概率理论中也有与此类似的情形。如果我们打算将p（a，b）诠释为对a的理性信仰的程度，那么b必须能表示信仰者能掌握的总体证据知识。
[34]对照我的《逻辑》附录*ⅸ“第三篇札记”。
[35]对照康德《任何一种能够作为科学出现的未来形而上学导论》［Prolegomena to Any Future Metaphysics that Will be Able to Claim Scientific Status］，1783年。粗体为康德原文所有，但我用“归纳理论”代替了康德自己的术语“形而上学”。
[36]我这里的这个论断（对照《逻辑》第28和80节）与C.G.亨佩尔所谓的“确证悖论”有密切的关系。亨佩尔似乎认为（见《心灵》，N.S.55，1946年，第79页），这些“悖论”仅仅是些“怪异的东西”，而“更深入的分析……将证明是合理的”，因此我们确实应当认可下述事实：白色的手帕或黑色的乌鸦确证了陈述“所有天鹅都是白色的”。可能他是对的吧，但我认为，所有这类“确证”或“证实”显然都太易得了，不能被认可为验证，因为它们一般情况下都不是反驳“所有的天鹅都是白色的”这个理论的真正尝试的结果。
亨佩尔的“确证”或“确证性实例”的概念（《符号逻辑学杂志》8，1943年，第122-143页）是“证实主义的”：这个概念告诉我们，陈述x确证陈述y当且仅当x描述了关于y的某一证实性实例。但由于亨佩尔的“逻辑要求”是不充分的，因此他的定义显然会产生下述无意的结论。令a是某一个体事物的名字，那么单称陈述“a是一只白色的天鹅”并不会像原先打算的那样仅仅确证“所有天鹅都是白色的”和“所有的非白色事物都是非天鹅”，它也会确证（我认为这肯定不是亨佩尔有意要得到的结果）“所有的事物都是白色的”、“所有的事物都是天鹅”以及“所有的事物都是白色的天鹅”，当然例外也是有的，那就是他特设地排除了的等式（我将在下文论述它们）“仅仅存在一只白色的天鹅”，也即“仅仅存在唯一的一个事物，而且它是天鹅”。另外，上面这个单称陈述能确证的仅限于与上述例举的陈述相容的那些陈述；因此它仅仅是在一种非常隐晦的意义上——“所有天鹅都是白色的，这乃是因为除了我们已经看见了的那只a之外就没有天鹅了”——确证“所有天鹅都是白色的”。这表明亨佩尔的定义显然是过于狭窄也过于宽泛。它确证了一些本来不打算去确证的陈述，却无法确证那些本来打算去确证的陈述。例如，根据亨佩尔的理论，下面两个陈述“任何人类都有一个人类的母亲”和“任何女性的人类都有一个人类的母亲”都是不能被人类确证的（虽然它们可以被“a不是人类”确证），而这是因为在亨佩尔的意义上，它们在人类中都不具有任何有限的“发展”［finite“development”］；但陈述“任何男性的人类都有一个人类的母亲”却可以被（例如）陈述“玛丽是爱德华的母亲（以及玛丽是一个女性的人类和爱德华是一个男性的人类）”确证。亨佩尔从他的模型语言中排除了等式，这就等于是防止人们用模型语言来表述那些显然不合直观的结论，但我并不认为这样做就能得出更为充分的定义。（另外对照J.W.N.沃特金斯，“分析的和经验的之间”［Between Analytical and Empirical］，见《哲学》［Philosophy］，1957年，第116-123页和第125-127页。）
顺带指出，有人批评我未能对“定律的实例化”和“定律的反驳性实例”给出“精确的”定义。其实我已在“关于塔尔斯基真理定义的札记”［Note on Tarski's Definition of Truth］最后一个脚注中给出了这些概念的“语义学的”定义，此文现在重印于《客观的知识》第335-340页。
[37]戴维·布鲁斯特爵士［Sir David Brewster］，《伊萨克·牛顿爵士的生平、著述和发现》［Memoirs of the Life，Writings and Discoveries of Sir Isaac Newton］，第二版，1860年，第ⅱ卷，第328页。
[38]见上文第13节注10和11对应的文字。
[39]对照《英国科学哲学杂志》12，1945年，第99页注2。
[40]I.康德，《什么是启蒙？》［Was ist Aufklärung？（What Is Enlightenment？）］，1785年。
[41]〈对照《无尽的探索》第7节对“透析”［dialysis］的讨论。编者注〉
[42]我曾在许多地方论述过这种方法论唯名论立场，并以此反对下述两种立场：其一是方法论本质主义，它询问和回答“是什么”问题；其二是形而上学唯名论，它断言有意义的词语仅仅是事物的名称（或事物的记忆图像），并因此从本质主义角度回答了（隐含的）本质主义问题——这也是错误的回答。
[43]M.石里克，“哲学的未来”［The Future of Philosophy］（见《哲学著述集》［Publicationsof Philosophy］，太平洋学院［College of the Pacific］编辑，1932年），这里的引文来自石里克的《论著全编》［Gesammelte Aufsätze］，1926-1936年（出版于1938年），第126页。石里克说，作为科学家，科学家的兴趣仅仅在于真理——在于证实——而非意义。但石里克随之又问，科学家如何能检验一个他并不知道其意义的陈述的真值呢？特别是如果某一陈述的意义正是它的证实的方法，那么情况又如何呢？在第127页中石里克写道：“一旦科学家发现了自己在其科学中使用的命题的隐含意义，他就成了一位哲学家。”作为例子他还提到了牛顿对物质概念的发现，以及“爱因斯坦对物理学中使用的术语‘同时性’的意义的分析”。我在《开放社会及其敌人》第Ⅱ章第ⅱ节中讨论并否决了后一个例子。至于前一个例子，即牛顿的质量概念（牛顿将其定义为密度在空间的积分），这是一个论述得非常糟糕的例子，如果牛顿在世的话必定会为之尴尬万分；实际上，除非我们作出下述假定，否则这个例子完全是不可理解的：石里克真正所指的不是牛顿的“物质”定义，而是物质的观念——连同一起的还有关于牛顿的重力理论的本质主义解释，而牛顿自己就拒绝了这种解释。我已经讨论过了这种解释，见我的“关于人类知识的三种观点”第ⅲ节，重印于《猜想与反驳》。
[44]关于苏格拉底问题（即柏拉图主义和历史上的苏格拉底之间的关系的问题）的讨论，见我的《开放社会及其敌人》第10章注释56，以及理查德·鲁宾逊［Richard Robinson］在《哲学评论》［The Philosophical Review］（60，1951年，特别是第494页及下页）中的文章。
[45]我猜想，对词语的力量——词语的魔力——的泛灵论信仰所涉及的正是儿童学习说话的那个过程；此过程联系他的经验——通过前语言的呢喃来控制周遭环境。我认为这种信仰涉及的是当我们谈论“词语的意义”时我们所指的那种东西；它或许可以部分解释有些人为何会觉得意义分析是重要的。在这里我们要感谢弗洛伊德，他深入探究了泛灵论及其关于“思想的全能”或符号和词语的全能的信仰。但弗洛伊德从未质疑过自己的本质主义研究途径中的泛灵论基础，他的晚期论文（《选集》5，1952年）就清楚地表明了这一点。在那里他研究了如何“更接近于本性，或人们有时所谓的心智的本质”这个问题（第377页），并宣称“意识不可能是心智的本质”，并进一步指出（这得益于T.利普斯［T.Lipps］）“心智本身就是无意识的，无意识就是真实的心智”（第382页）。这个多少有点无意义的讨论（无意义是因为询问心智的本质就如同询问白兰地酒中的“酒精之魂”［spirit］或灵魂中的灵［anima］一样；如果无意识就是心智的本质，那么心智的活力有可能就是无意识的本质，而利比多［libido］有可能就是心智的活力的本质，等等）中最有价值和意义的地方可能就在于弗洛伊德认识到（第378页），物理学家可能不会问“什么是电的本质？”弗洛伊德知道在这里产生了矛盾，因为“心理学也是一门自然科学”。弗洛伊德打发掉了这个矛盾，但不是依据他那多少有些含糊的论证。他表明在心理学中上述“情形是不同的”，因为“所有人的行为都类似于……业余心理学家”，也因为所有业余的心理学家都相信科学；当他说出这些观点的时候，他已经非常接近于（但还不足以）说本质主义是一种前科学的态度，并由此揭露其魔法的和泛灵论的根源。
[46]休谟谈论过关于词语的“精准的阐明”（例如“力量”这个词；对照其《人类理解研究》第ⅱ部分第ⅳ节的脚注），而他指的意思是“确定〔某个词语〕的意义”并“由此将那些在哲学中令人头疼不已的晦涩不明的部分去除掉”（前引书，第ⅶ节）。
卡尔纳普在《概率的逻辑基础》（1950年）第一章“论阐释”［On Explication］中提到了康德、胡塞尔、摩尔和朗格福德［Langford］。他特别明确地假定，“是什么”问题是相关的问题；他批判的仅仅是那些不首先确保“问题的术语”是充分清晰或确切的就“开始去寻找答案”——即“是什么”问题的答案——的人（第4页）。在他看来，“阐释”某一“被阐释项”这个任务可以被定义为将被阐释项转换为（或代之以）某一确切的概念，即阐释项。
[47]见《逻辑》第19节注释2，以及《开放社会及其敌人》第2章第ⅱ节（参见《历史决定论的贫困》第10节）。〈对照《无尽的探索》第7节。编者注〉
[48]伯特兰·罗素，《神秘主义和逻辑》，1918年；对照第ⅴ章倒数第二段。
[49]塔尔斯基《逻辑学、语义学和元数学》［Logic，Semantics，Metamathematics］，1956年，第299页。
[50]对照R.库兰特［R.Courant］和H.罗宾斯［H.Robbins］，《什么是数学？》［What is Mathematics？］，1941年，第433页。
[51]参见贝克莱，《分析者》，1734年，第47节。（粗体为我所加。）
[52]《分析者》，第8节。
[53]〈见《客观的知识》，前引书，第128-140页。编者注〉
[54]见《伯特兰·罗素的哲学》，P.A.希尔普编，1944年，第13页。要注意的是，G.E.摩尔讨论罗素的“描述理论”的论文（前引书，第177-225页）根本就没有提及罗素理论所意图解决和已经解决的任何问题，但另一方面，摩尔认为他的主要任务之一就是去考察，究竟是什么理由让F.P.拉姆齐［F.P.Ramsey］将罗素的理论描述为“哲学的范例”。换而言之，摩尔想评估罗素的理论。但问题是，如果不将理论与它意欲解决的问题联系到一起的话，没人能了解此理论的价值。我非常尊敬摩尔，认为他是一名实在论者，也是常识的捍卫者。但我无法尊敬地将他看作一位分析者。他的这篇论文现在被许多人称赞为分析的范例，但其中却很少对罗素的理论提出批判或改进，而且与罗素的理论意欲解决的问题毫不相干；我觉得这种文章已经造成了灾难性的影响。它已在鼓励人们去仿效它而忽略了下述箴言：如果我们希望我们的批判能有价值的话，我们就应当不断地去批判某一理论的最强形式，而不是抨击它呈现出来的最小的弱点。因此，这篇文章也降低了哲学讨论的标准——要知道，这个标准本来就岌岌可危了。
[55]见《逻辑》第32节和第38节以下。
[56]参见我的对话体文章“日常语言中的自我指涉和意义”，《心灵》63，1954年，第162页及以下各页；现在重印于《猜想与反驳》。〈见波普尔对塔尔斯基的讨论，见《猜想与反驳》第10章，以及《客观的知识》第2和9章。编者注〉
[57]塔尔斯基的工作已经鼓励人们去作出如下主张：当我们希望能给出“确切的”定义时我们就必须去构造出某种人工语言模型。但我不认为这个主张正确地诠释了塔尔斯基的工作，因为他的理论适用于非常普适的集合中的所有语言。
[58]有用的定义——能够帮助我们解决真正问题的那种定义——永远都是消除性定义而非上文提及的阐明性定义，哪怕总要强调说我们的研究通常都是由直觉来引导的。但可以引导我们提出定义的种种意义的直觉只是我们自己的私人之事，至于是否认可这定义得看它能否产出丰富的成果——能否帮助我们获得问题的解答。（a）消除性定义和（b）阐明性定义之间的差别密切对应着我在其他地方所论述的（a）从右向左的定义和（b）从左向右的、或曰本质主义的或亚里士多德主义的定义之间的差别；见我的《开放社会及其敌人》第11章第ⅱ节。〈对照《无尽的探索》第31页。编者注〉
[59]我相信这些论述能够澄清所谓的“分析悖论”，因为照我的观点，这个“悖论”可以诠释为它表明了分析（或定义，我指的是不同于给某个长篇故事写一个简短标题的那种定义）总是无价值的，除非某一定义问题——我们认为分析能有助于问题之解决的那种问题——能表明在“分析项［analysans］”（或定义项）中这种类型的术语是可被接受的。
人们通常用分析性定义来描述分析悖论，“一个兄弟是一个男性的兄弟”就是佳例，而且摩尔自己也认可这个陈述。我还曾找到一些可能更有启发性也更具娱乐性的例子，但其目的惊人类似——这些例子见于一本广泛散发的小册子，它由大都会警察驾驶学校［Metropolitan Police Driving School］编辑，英国皇家文具署［Her Majesty's Stationery Office］1955年出版，并献给大都会警察局局长［Commissioner of Police of the Metropolis］。标题是《驾驶技巧：机车编队学员驾驶指导手册》［Roadcraft：A Manual of Driving Instruction for Students of the Motor Car Wing］，而它非常关注于阐明和意义分析，下面这些极具代表性的引文就表明了这一点：
“5.注意力集中可以被定义为将心智和身体完全集中于特定的行为之上，排除一切与此行为不相干的所有外物。”（第7页。）
道德哲学家们可能会对下文中包含的“好判断”的分析感兴趣：
“8.在视觉、听觉、健康身体素质和注意力集中的帮助下，驾驶员将可以做到好判断，它意味着有能力区分正确的和错误的、好的和坏的、安全的和危险的。”（第7页及下页。）
下面两个句子是直接定义的范例：
“15.这个意义上的努力可以被定义为力量的施行。”（第11页。）
“18.侧滑的定义如下：轮胎对路面的抓力变得小于作用于车辆的某种力或几种力，从而导致车辆的非有意运动。”（第18页。）
我断言要对这种空洞措辞承担最终责任的应该是哲学和哲学家，而不是警察局长。而且我相信没有哪位严肃的观念史学者会质疑我这一断言。