31 验证
那些坚持某种理论而又没有批判意识的人,其问题就在于他们往往倾向于将任何东西都看作对理论的支持或“证实”,而不把它们看作对理论的反驳。许多经验论者都看到了其中的危险,例如培根;但经验论者为了扭转上述局面而忠告科学家们,一定要禁绝理论行为,抛弃所有“先入为主的”理论,直到纯粹的、无偏见的观察产生出某种理论并强加给心智。我们已经知道,这个忠告是不合实际的,只能导致自欺,养成无意识地(因而也是不加批判地)坚持自己理论的习惯。给科学家们的正确忠告是这样的:你可以一直有意识或无意识地坚持自己的一整套理论,但你也应当采取一种批判的态度来对待它们,哪怕你在通常情况下无法同时积极地批判一个以上的理论。
如果一个人认为,当某一事件或观察(称为e)“遵循”某一理论或假说(称为h)或是h的某一实例的时候,e就是在支持或确证h,那么他就等于是采取了一种非批判性的态度。
这些人会不加批判地相信,出现了一只白色的天鹅就是在“支持”或“确证”假说h1“所有的天鹅都是白色的”。但假说h2“90%的天鹅都是白色的”又如何呢?h1说所有天鹅都是白色的,因此h2和h1显然不一致;但如果出现了一只白色的天鹅可以被视为在“支持”h1,那么对后一个假说也应当同样来看待。[12]有人也许会答复说,为了支持统计理论h2,我们需要一个至少有10只天鹅的样本——其中九只白色的,一只非白色的。但如果确实如此,那么我们也可以说,为了支持h1,我们也至少需要相同数量的、(当然)全部是白色的天鹅,难道不是吗?(但果真如此,那么一个实例就永远无法支持任何理论。)
我们将稍后再讨论像h2那样的统计理论问题,现在我们只考虑全称理论。
在此我们考虑两种主要态度:
(a)非批判性的或证实主义的态度:寻求的是“证实”、“确证”或“实例化”,而且往往都能找到它们。所有被观察到的理论“实例”都被认为是在“确证”该理论。
(b)批判性的或证伪主义的态度:寻求的是证伪或相反实例。[13]只有在拼命寻求反例而无所获之后我们才能说这是对理论的验证。
有人也许会问,将理论的所有实例都视为对理论的确证,这真的就是非批判性的态度吗?然而从逻辑上可以表明,这样做就等同于相信所有一切都是确证——除了反例是唯一的例外。因此不单是白色的天鹅,黑色的乌鸦和红色的鞋子也同样“确证”了理论“所有的天鹅都是白色的”。这可能看起来很怪异;但如果这是真的,人们必须承认那些将所有一切都视为对其理论的确证的人,从证实主义的观点来看确实是很正常的,而且反之亦然:证实主义者就是那种倾向于将所有一切都视为支持自己观点的人。
可以很容易地表明,所有一切确实都是“所有天鹅都是白色的”的实例——除非它是一个反例,也即一只非白色的天鹅。因为“所有天鹅都是白色的”可以写成“所有是天鹅的东西都是白色的”、“如果某种东西是天鹅那么它是白色的”或“所有东西都是白色的除非它不是天鹅”。任何满足此公式的东西都是一个“实例”。我们都知道(存在逻辑中),任何不是天鹅的东西都满足这些公式,任何是白色的东西也都满足它们;因此只有既是天鹅又非白色的东西(因此是一个反例)不满足它们。这表明了证实或实例化太易得了,根本没有价值,这也表明了只有被期望存在反例的情形才是有价值的,除非理论确实为真。更精确地说,有价值的情形只能是关键情形——在此情形中,被检验的理论所预测的结果不同于其他有价值的理论所预测的结果,特别是不同于那些至今为止都得到认可的理论所预测的结果。
因此可以说,证实主义的“支持”和我自己的“支持”之间存在根本差别。证实主义观点主张,h的所有“实例”都支持h;而我则断言,只有真正检验的结果才能支持h。
因此在证实主义者看来,一只被观察到的白色天鹅支持理论“所有天鹅都是白色的”;如果他是一致的(像亨佩尔那样),那么他会说一只被观察到的黑色鸬鹚也支持这个理论“所有天鹅都是白色的”。而在我看来,这些观察都不一定支持这个理论,虽然在特殊情况中每一个都有可能支持它。因此,如果我们(依据先前被接受的理论)有好的理由认为池塘中的这个东西是一只黑色天鹅,那么当我们发现这是一只白色天鹅或发现这是一只黑色鸬鹚,我们的发现就确实有可能支持理论“所有天鹅都是白色的”。
在证实主义者看来,由此存在着一种简单的形式逻辑关系——实例化的在场或不在场决定了e是否支持h:如果e是h的一个实例,那么e就支持h。但在我看来情境更为简单:仅当e是对h真正、诚挚的反驳的结果时,e才能被视为对h的支持。
我不认为我们可以从逻辑上完备地分析e和h之间的关系:“真挚”不是能进行逻辑分析的东西。但我们也没有理由气馁。首先,我们不需要对支持和验证进行逻辑分析也行。其次,我们也可以足够好地去分析它——比我们能想象到的还要好。
我将更为充分地分析“e支持h”这个概念,以准备随后再对e验证h的程度进行分析。为了达到目的我们将使用除了e(经验证据)和h(假说)之外的另一个变量:我们的背景知识b。这样我们就可以说,e根据b支持h。[14]
我们的背景知识b指的是我们在检验h时所持有的——可能仅仅是暂时持有的(与问题情境相关的)任何知识。因此b也有可能包括初始条件。重要的是要认识到,b必须与h一致;因此,如果我们在考虑和检验h之前接受了某个理论h',而它与h或我们的其余背景知识一起是不一致的,那么我们就必须从背景知识b中排除h'。(判断什么是我们必须从b中排除的,这并不总是件容易的事情,但我不打算在这里讨论这个问题。)
让我们假定手头有一些hb——即h和b的合取——在实验上可检验的结论。在这些结论中存在一些事件,如果h是假的,那么在我们的期望中就可以确定它们不会发生。e就是这样的一个结论;也就是说,e描述了一个可观察事件,(在给定b的前提下)如果h是真的,在我们的期望中它将会发生,而如果h是假的,在我们的期望中它将不会发生。那么我们就会说,如果e实际上发生了,那么这就可当作对h的支持。
当然,上面的表述并不非常令人满意,它仅仅是我们进行讨论的起点。令人不满意之处就出在e这个事件的性质上(我们曾叙述过两次)——“如果h是假的,在我们的期望中它将不会发生”。
我们的要求是“(在给定b的前提下)可以从h中推出e”,有人也许会将之诠释为下述要求:“(在给定b的前提下)可以从非h中得出非e”。但这等同于另一种形式的证实主义:它将使e和h相等价(在给定b的前提下),并因此允许我们用观察——即观察到e是真的——来证实h。
而且,即便不是故意要针对证实主义作文章,我也要指出“可以从非h(和b)中推出非e”这个主张是完全不合理的,理由如下。假定e是一个支持h的事件,也即h所预测的某个事件,如果没有h我们就根本不知其存在的某个事件。例如,令e是伽勒[J.G.Galle]在亚当斯[Adams]和勒威耶[Leverrier]预测的位置上对一颗新行星(海王星)所作出的观察,而令h是亚当斯和勒威耶作出预测所依据的牛顿理论。那么e当然支持h——而且是非常强的支持。但是在另一方面,(在给定b的前提下)从其他蕴涵非h的理论中(例如爱因斯坦理论)也可以推出e。因此要求应当能从非h(和b)中推出非e,这是非常错误的,这个错误等同于下述信念:e(我们曾说过它在h和某些其他有意义的理论中必定是关键的)在h和所有其他与h相矛盾的理论中必定是关键的。
基于这个理由,第二个要求“可以从非h(和b)中推出非e”就太强了。但如果完全不考虑类似的主张,那我们也什么都做不了。因为我们的第一个要求——可以从h(和b)中推出e——是非常不充分的,这是基于如下考虑:如果能单独从b中推出e,那么在给定b的前提下,也可以从h中推出e。
但另一方面,如果要求不能单独从b中推出e,这也是不充分的。因为如果在单独给定b的前提下e是概然的(在概率计算意义上的“概然”),那么我们就不可能将e的出现视为对h有意义的支持。
这些道理可以解释下述事实。实际上,詹姆士·查理士[James Challis]在得到了亚当斯的计算数据后,先于伽勒在计算出的轨道附近观察到了海王星。但他发现这颗星星似乎是静止不动的,从而也就认为自己的观察没什么意义——其实如果他再做几次观察也许就能发现它是运动的了。在计算区域中观察到某颗八等亮度的未知星体,这件事在他的背景知识中非常概然,因此在他看来也就不具备什么意义。只有观察到一颗运动的星体,一颗运动的行星,这才有意义,因为这种观察是非期望的——不过在亚当斯的计算中并非如此。[15] 因此我们可以作出如下假定:在给定背景知识的前提下,某一事件的非期望性在概率计算的意义上等同于低概率。
因此有必要作出第二个要求,根据此要求,我们应当排除下列情形:在单独给定背景知识b的前提下e是概然的——这里的“概然”取概率计算的意义。
因此我们需要概率计算;我们可以写出
它的意思是“在给定b的前提下a的概率等于r”。同样地,我们也可以将“a和b”的合取写成“ab”,将“非a”写成ā。于是
的意思是“在给定c的前提下a和b的概率等于r”;而下式
的意思是“在给定b和c的前提下非a的概率等于r”。
现在,我们可以将我们的要求“经验证据e如果将支持h的话,在单独给定背景知识b的前提下它就不应当是概然的(或被期望出现的)”写成
这让我们立刻认识到,p(e,b)越小,e对h的支持力度就越强——前提是我们的第一个要求应得到满足,也即在给定b的前提下可以从h和b中或从h中推出e。
这个结果有两个意义。第一,它在直观上是非常令人满意的,因为只有非概然的证据e——在我们的背景知识中非概然的——才会被我们接受为有意义的,海王星的例子就表明了这一点。如果一个算卦的跟一个年轻姑娘预言说“你很快就能遇到一位让你心动的绅士了”,那么这个预言本身就太概然了,没什么接受的意义,它很容易就能为真,并支持算卦占卜所依据的理论。从直观上我们要求只有严格的检验才能算数,而且检验越严格,它们的意义就越大。这个要求就等同于说,根据我们的背景知识e应当是非概然的。用概率语言明确表述这一点就是:e应当是严格的检验的结果。而这本身又涉及到下述要求:h应当是高度可检验的——即可以为严格的检验所检验,因此应当是高度非概然的,或具有丰富的经验内容。
所有这些思考表明,下述关于“e支持h”的定义应是合理的:
在给定背景知识b的前提下e支持h当且仅当:
(a)可以从hb推出e
(b)p(e,b)≪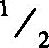
显然我们可以像(b)一样将(a)写成概率术语的形式;也就是说,我们可以用另一个稍弱[16]的表述“在给定hb(即h和b的合取)的前提下e的概率等于1”来代替“可以从hb中推出e”。这样的话我们有
(a) p(e,hb)=1
考虑(a)和(b),我们可以进一步修改(和减弱)我们的定义,从而得到:
在给定b的前提下e支持h,当且仅当
(c) p(e,hb)-p(e,b)>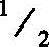
要顺带指出的是,写成此形式后,“甲支持乙”变成了另一种更强的含意“乙肯定性地依赖甲”;因为一般条件下我们都可以在概率理论中作出如下定义:
在给定c的前提下b肯定性地依赖a,当且仅当
p(a,bc)-p(a,c)>0(https://www.daowen.com)
实际上,我们就可以用此式来定义“支持”,更确切地说,我们可以用下述更弱的定义来代替(c),即
(d) p(e,hb)-p(e,b)>0
以上述方式,我们得到了《逻辑》附录*ⅸ三个注释中的第一个注释(第396页)所给出的关于“支持”的定义(的相对化形式)。
在我看来定义(d)是相当充分的,只要我们给它补充一个附加条款以代替(c):
e给h的支持是有意义的,当且仅当
(e) p(e,hb)-p(e,b)≫½
随着这个附加条款的提出,实际上我们已经进入了支持的程度问题或验证度的问题领域之中了。因为通过定义(d)及这个附加条款,我们不但还未得到“支持”的强定义,而且又得面临着决定支持的有意义的程度问题;换言之,我们必须引入对支持的程度或验证度的度量,以区分各种有意义的程度。
作为第一步,一个比较显而易见的可能做法是这样的:在认可附加条款的同时,我们可以利用(c)和(d)之间的差,也即
(f) p(e,hb)-p(e,b)
作为在给定b的前提下e给h的支持程度的度量,或是在给定b的前提下e对h的验证度(C)的度量;也就是说,我们通过(f)所表明出的差,把在给定背景知识b的前提下e对h的验证度定义为
C(h,e,b)
这个定义还有一些瑕疵,但我们可以通过“形式化”(e)来弥补——用下述“形式化分母”来除(e)
(g) p(e,hb)-p(eh,b)+p(e,b)
于是我们得到了下述定义
![]()
在这个定义D中,分子(e)具有明确而简洁的直观意义,但分母(f)则没有这样的意义:我们选择它仅仅是因为它能带来令人满意的结果——它能消除前面提到的瑕疵——而且看来也是能得到此结果的最简形式化分母了。
在指出D所能消除的一个瑕疵之前,我将给出一些(f)或D能产生的一般结果。
无论是采取D还是采取(e)[17]来作为验证度的定义,我们都能得到下述高度直观的结果:
(ⅰ)如果(在给定背景知识b的前提下)e支持h,那么C(h,e,b)是肯定性的。如果e推翻h(因此非e支持h),那么C(h,e,b)是否定性的。如果e二者都不是,这样的话它在给定b的前提下对h是独立的,那么C(h,e,b)等于零。
例如,如果e是一个重言式或b的某一逻辑结论,那么e既不验证也不推翻任何理论h,并且C(h,e,b)将等于零。同样地,如果h是一个重言式或b的某一逻辑结论,那么任何证据e都不会验证或推翻它,同样地也有C(h,e,b)=0。
(ⅱ)C(h,e,b)的最大值能达到1。它达到这个值当且仅当
(aa) p(e,hb)=1
(bb) p(e,b)=0
这个结果是高度令人满意的:只有在给定背景知识b的前提下极端非概然的e才能给h最大的支持,或最高的验证度。当然,为了做到这一点,我们必须能在给定b的前提下从h中推出(或“几乎推出”)e;也就是说p(e,hb)必须等于1。从根本而言,为了使h是最高可验证的,h的内容或可检验度必须是最丰富的或最高的;也就是说,如果验证度要达到最大值1,下述进一步的条件必须要得到满足:
(cc) p(h,b)=0.
实际上,(cc)是(aa)和(bb)的一个直接结论。[18]
(ⅲ)更一般的是,如果p(h,b)≠0,那么C(h,e,b)能获得的最大值等于1-p(h,b),因此也等于h相对与b的内容或h的可检验度。这使得可检验度等于h的最大验证度值,或等于h的“可验证性程度”。
迄今为止一切都很好,但还是存在瑕疵:如果在给定b的前提下某一经验证据e证伪了h,那么情形会如何?如果e报告的是严格检验的结果——例如一次非常精确的测量——那么它相对于b就有可能是极端非概然的;这就是说,在此情形中不但p(e,hb)=0,而且近似地还有p(e,b)≈0。这样一来,如果我们采用(f)作为定义的话,支持的程度或验证度就会变成零(或非常接近于零)。但如果我们采用D,那么当(在给定b的前提下)e证伪了h时,支持程度或验证度就会永远等于-1。也就是说,从D我们可以得到:
如果e与hb不相容,那么
C(h,e,b)= -1
这显然也是令人满意的,而且它还消除了定义(f)本身固有的瑕疵。对于所有h(假定它与b一致)它都能使验证度的最小值等于-1,而使其最大值等于h的内容或可检验度(h的最大值是+1)。
(重印于《逻辑》附录*ⅸ的三篇札记还详细说明了其他令人满意的方面;特别见第一篇札记第9节陈述的九条“预设条件”[desiderata]。)
还有许多不同于D的定义,而且从某些角度看,其中某些比D更优选。实际上我的第一个定义[19]就与D稍微不同。我优选D是因为在能满足我的“预设条件”的各种公式中它最简洁,也最明晰。但若是着眼于某些特定目的,那么某些算术公式也许能做到同样好——甚至更好。
所有这些令人满意的公式的重要特点是这样的:看来它们都是“拓扑等价”的;也就是说,如果采纳D,同时对于某个h,e,b,和h',e',b',我们有
C(h,e,b)≥C(h',e',b')
如果采纳任何其他令人满意的定义,上述关系也依然成立。而在哲学上这就意味着在它们之间进行选择是任意的——除非是着眼于简单性和明晰性。
但是,对于所有“令人满意的”定义——也即所有那些与D拓扑等价的定义——我们都有下述定理:
验证度不是概率;也就是说,它不满足概率计算规则。[20]
现在人们已普遍认可这一点了,只是有些人仍然坚持认为“可接受性”与“验证”不同,认为“可接受性”就是概率。当然我们也可以将“可接受性”(或“认证”)定义为概率。但如果我们是从经验科学的角度——也即从经验科学的目的这个角度——来看待理论h的可接受性,认为它是h令人满意的程度的话,那么可接受性必定与验证逻辑等价。重言式具有最大的概率值,但它们在经验科学中不可接受:确定某一据称的经验理论是(或几乎是)重言式的,这总是等同于对它进行了决定性批判。
因此我不否认下述观点:概率的逻辑诠释或陈述的概率可以使陈述的概率值、似然性或偶然性为真,而只要它这么做了,它也可以使“可接受性”程度为真——假设当我们谈论某一陈述是“可接受的”时,我们指的是相信它为真。但是,当我们在科学中接受某一陈述时,我们完全不是这个意思,下述事实就显然表明了这一点有价值的理论总是具有可忽略不计的概率(如果不为零的话)——甚至那些当前被我们广泛接受的理论也是如此。
在本节的最后,我将给出七点来总结我对验证的观点和看法,其中第一点是最根本的。
(1)某一理论的验证度就是对此理论所能经受的经验检验结果的评估。
(2)在对待理论和经验的关系时,人们有两种态度或曰两种看法:其一是寻求确证,而其二是寻求反驳。(显然,第一种是护教论[或教条主义]的态度,而第二种是批判的态度。)科学检验总是试图进行反驳。
(3)虽然不是完全地,但大体上我们都可以用逻辑分析来考察试图确证和试图反驳检验这二者之间的差别。
(4)我们可以说,某一理论被验证的程度越好,那么它所经受的检验就越严格(它也能更好地通过这些检验)。
(5)我们可以说,检验越是严格,不能通过检验的概率就越大(这概率既包括绝对概率或先验概率,也包括我所谓“背景知识”中的概率——所谓“背景知识”就是指在检验被考察理论的过程中不被人质疑的、作为共识的知识)。
(6)因此,从直观上说所有真正的检验都是试图去给理论“下绊子”:它不但是一场严格的考试,而且是一场不近人情的考试——它的目的在于使考生们落败考场,而不是给考生们机会去展示他们所知道的东西。展示所知的态度是那些打算去确证或“证实”其理论的人的态度。
(7)假定我们总能基于一种真正的批判态度去接受检验的指导,而且总能竭尽全力去检验理论(这个假定是无法被形式化的)[21],那么我们就可以说,假设我们根据理论所作出的预测是成功的,那么这个理论的验证度就会随(依据背景知识而得出的)非概然性的增加而增加。[22]
