对主观理论和逻辑理论的进一步批判
在开始分析单一事件的客观概率之前,我打算从稍微不同于前面章节的观点出发,对主观理论和逻辑理论再做一些批判。
我很乐于承认,我们当然可以毫无问题地将概率计算诠释为针对理性期望程度(或类似的东西)的计算,而在这样做的时候我们既可以采用主观或心理学的方式(例如拉姆齐、古德或开米尼),也可以采用逻辑的方式(例如杰弗里斯、凯恩斯或卡尔纳普)。[41]
在这里我打算批判下述观点——它认为上述诠释正确地阐述了概率在物理科学中的用处。
在我看来,物理中的陈述是客观的,在任何程度上它们都不涉及我们的信息状态:它们既不“表述”我们的信息,也不“表述”我们的无知。它们是一些关于世界的断言——当然这是猜想性断言。
这一点对物理科学中的概率陈述也适用。它们不是我们缺乏知识的产物。知识的缺乏不会奇迹般地产生关于频率的知识——即便在大数律的帮助下也不会。
频率假说——例如关于光谱线密度的频率假说——和其他所有物理假说一样客观,那些否定单一事件概率客观性的人也可能承认这一点。但我认为,这其中的差别相对而言是很轻微的。客观的单一事件概率产生了(依据波莱尔—坎特利定律和杜布定律)客观的频率陈述。另一方面,表述了合理信仰状态的概率只能产生涉及合理期望频率的陈述;如果诠释是主观的,那么“合理期望”就是主观的,而如果原来的诠释是逻辑的或重言的,那么“合理期望”就是逻辑的。
在单一事件客观概率的情形中,我们首先在单一事件会发生的前提下估计其客观条件;然后我们用数学推导的方法,在特定频率会发生的前提下估计其条件。在主观概率和逻辑概率的情形中,我们首先估计的是“数据”——即信息“给定”的陈述——与事件陈述之间的逻辑关系;然后我们用数学推导的方法[42],估计这些同样的数据和特定频率陈述之间的逻辑关系。这样一来,我们所获得的东西仍然与我们的信息相联系;我们并未能像客观概率假说的情形一样,推导出频率假说,从而检验它或者视需要否定它;我们获得的是(假定计算是正确的)真的陈述(实际上是重言陈述),它涉及的是我们给定的知识确保特定频率的期望的程度:我们得到的不是物理猜想,而是关于我们自己知识状态及其内容的自明之理[truism]。(见前一章。)
再来考虑骰子的情形。主观理论和逻辑理论并没有真正地去处理物理学家们所关注的下述问题:这粒骰子的行为如何?这两个理论并不能真正产生下述问题(当然这问题是不可回答的):下一次投掷会是哪一面朝上?它们询问的是另一个不同的问题:“我们的数据在什么程度上允许我们作出关于这粒骰子行为的某种陈述?”在涉及到下一次单一事件时它们也只能询问:“我们的知识(或无知)在什么程度上允许我们预测下一次投掷将得到一点?”[43]
我关注的是骰子的行为,而我相信大多数物理学家也是如此。我想了解它的秘密,我准备提出某种猜想——例如,在特定条件下作出的长投掷序列中它每一面朝上的频率都是相等的;又或者,这些条件确立了所有面都是对称的。(https://www.daowen.com)
与此相反,主观的和逻辑的理论家们关注的是他们已经对这粒骰子了解了多少,而不是关于它行为的猜想。例如他们会发现,至于下一次投掷结果究竟是六个面中的哪一面朝上,他们都是一样的无知,因此这六个概率是相等的。
假设我们现在有了一个投掷序列3、1、5、1、2、2、3、5。主观的和逻辑的理论家们必定断言,这些新的数据肯定会影响下一次投掷的概率。下一次的概率将或多或少地改变:发生4和6的概率会(或多或少地)减少,而发生1和2的概率会增加,因为4和6根本就没有发生过,而1和2各发生了两次。
现在假定这粒骰子是同质的,那么这个序列就变成一个正规序列。那么主观诠释和逻辑诠释意义上的概率将一直都发生轻微变化,并最终逐渐接近于等分布。长投掷序列和新“数据”的总体影响是零。因此这个数据将变成“基本上不相关的”。[44]
另一方面,从客观理论——无论是单一事件还是频率类型——来看情境都大不相同。从这个角度来看,投掷序列构造了一个对假说的统计检验。如果我们从一开始就怀疑骰子有问题,那么检验将会反驳我们的怀疑。因此我们就可以宣称,它验证了我们关于等概率的猜想。
根据这个观点,主观诠释和逻辑诠释混淆了有关客观物理系统的物理陈述,以及“我们的经验支持”这些陈述程度的认识论估计。
要对这个错误负责的,不仅是“所有单一事件理论都必定要么是主观的要么是逻辑的”这个错误信念。新的“信息”有可能以多种方式改变概率,这个无可置疑的事实似乎也让许多理论家相信,概率不可能描述实验条件的客观特性:如果我们“被告知”投掷结果是一个偶数,那么投掷两点的概率就是⅙或⅓,用符号来表达就是:
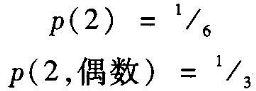
无疑事情确实如此。但这个公式在将“偶数”这个词诠释为“信息”时,它已经采用了一种主观或逻辑的诠释。(这不意味着在客观理论的上下文中我们也无法使用“信息”这个术语,我们只需提防不要被术语所误导,混淆了两种诠释。)
从客观观点来看,“p(2)”和“p(2,偶数)”涉及的是两个不同的实验安排:前者涉及的是考虑了所有投掷的实验安排,而后者涉及的是我们决定忽略那些结果为奇数的投掷的实验安排。因此我们也可以这样说:符号“偶数”所表述的“信息”告诉我们,我们在询问的是一个不同的问题——我们不再去问“投掷两点的概率是什么”,而是去问“在只考虑那些结果为偶数的投掷前提下,投掷两点的概率是什么”。[45]
