新经典理论和频率理论的对比
新经典理论和先前的经典理论一样,都将概率视为可能性(或特性、类或集)的测度。但它和经典理论的差别还是很大的,如下所述。
(a)它不以概率定义作为起点。相反,它把“概率”看作任何满足特定计算规则的东西。
(b)它不认为等分布或等概率比非等分布更基本。
(c)在许多非常重要的情形中,它都断言,特定可能序列的集具有0或1测度,并用这一定理取代了特定经典极限定理(其断言内容为:某些概率倾向于极限0或1)。
(d)它也允许其他诠释,但它强烈地支持——特别是通过其独立性理论——下述诠释:概率属于单一的出现或事件,而检验概率的手段是这些事件重复序列中的频率;也就是说,它支持概率的趋向性诠释。
下面我将依次简要阐述这几个要点。
(a)我们应当记得(对照《逻辑》第48节),经典理论[27]将概率定义为有利的可能情形与同等可能情形的比例。“同等可能的”在这里也意味着“同等概然的”,因此这个定义也就是要用等概率来定义非等概率;换言之,它等于这样一种看法:概率计算应当将等概率视为其基本概念,应当在这些基础上构造出一般计算规则。我将在(b)中更详细地讨论这个看法。
与此相反,新经典理论不打算采取拉普拉斯或冯·米泽斯的“概率”定义。它明确区分了两种任务,其一是构造概率数学计算的形式任务,其二是诠释这种计算在机遇对策中的一般应用。
拉普拉斯和冯·米泽斯在定义概率时都想到了应用层面。拉普拉斯想到的是骰子的六种概率,而冯·米泽斯考虑的是一个奇怪的事实:在投掷的长序列中,骰子出现的点数是无概率性的,但都是等频率的。因为在新经典理论中,“概率”意味着满足形式数学系统规则的任何东西。所以我们应当首先给出一个系统(同时着眼于数学的普遍性和可能的应用性)。至于对它进行不同诠释的问题则是后起的。
(b)新经典理论不以等概率的优选状态为假设,尤其是它不打算将所有概率构造为终极的等概然的“单位”或“位”的总和,换言之,它不打算将所有概率构造为计数可能性[counting possibility]的实际结果。
与此相反的观点还很流行[28],例如常有人说只有唯一一种方法能估计概率的实际数值。考虑到这一点,我认为有必要补充几点批判意见。但首先我想重申的是我以前认可的一个观点(对照《逻辑》第57节):等概率的假说性估计适用于对称的情形,它在物理学中非常重要。([29]当然,我们无法从无差别原则中推导出这些估计,它们也不是可推导的;但正如所有假说一样,我们完全可以依据自己的直觉来猜想其内容(包括下述有趣的事实:等分布最大化了预测的不确定性)。
我的第一个意见是(正如冯·米泽斯常常强调的),哪怕是灌铅骰子这种简单情形——这显然是与物理学相关的问题——也超出了等概率问题的范围。
第二,我们应当知道,许多坚持经典概率理论的人(包括拉普拉斯自己),虽然一开始是从德莫弗的定义出发,但后来(有时就在写下这个定义之后)都发展出了某种完全与等概率假定独立的、更为普遍的理论,例如直接给出了二项式公式的一般形式。
第三,雅妮娜·霍西亚松[Janina Hosiasson]的批评[30]值得我们重视。其观点考虑了下述两种非常类似的机遇对策之间的差别。
第一种机遇对策可以描述如下:
我有一只袋子和两个盒子,称为一号盒子、二号盒子。在袋子里有三个计数器,其中两个标着“一号”,另一个标着“二号”。在一号盒子和二号盒子中各有三个球;在一号盒子中,有两个球是白色的,另一个是黑色的;在二号盒子中,有一个球是白色的,另两个是黑色的。
我们从袋子中随机抽取一个计数器。如果它标着“一号”,我们就接着随机从一号盒子中抽取一个球;如果它标着“二号”,我们就接着随机从二号盒子中抽取一个球。当我们已经从不论一号盒子或二号盒子中抽取了一个球后,游戏便结束。现在请问抽中白球的概率。
答案当然是:
第二种机遇对策可以描述如下:
第二个游戏和第一个游戏完全相同,除了在二号盒子中只有两个球,一白一黑。
在此情形中,抽中白球的概率也很容易算出:
比较这两种对策,我们可以将第一种表示为以下图表:
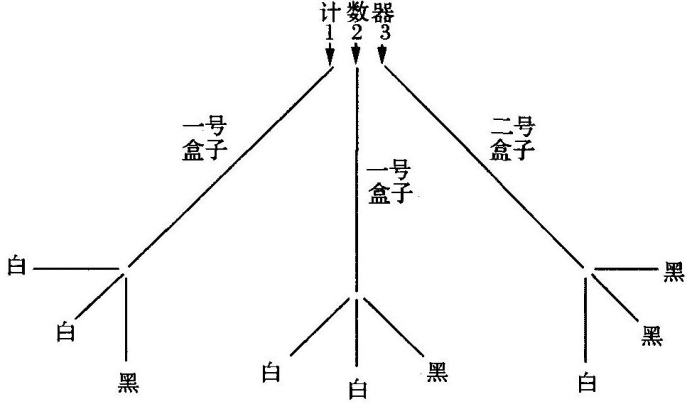
而第二种对策的图表如下:(https://www.daowen.com)
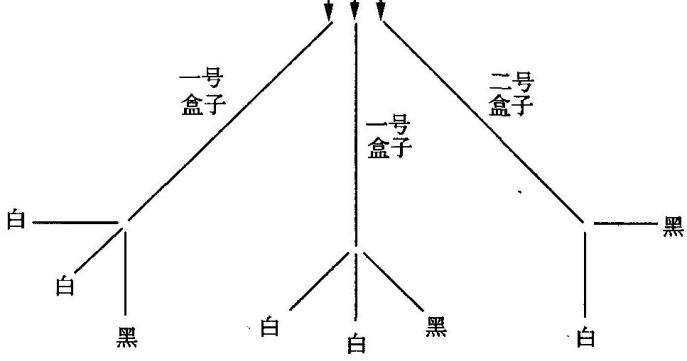
我们对第二种对策结果的计算可以表示为下面的第三个图表:
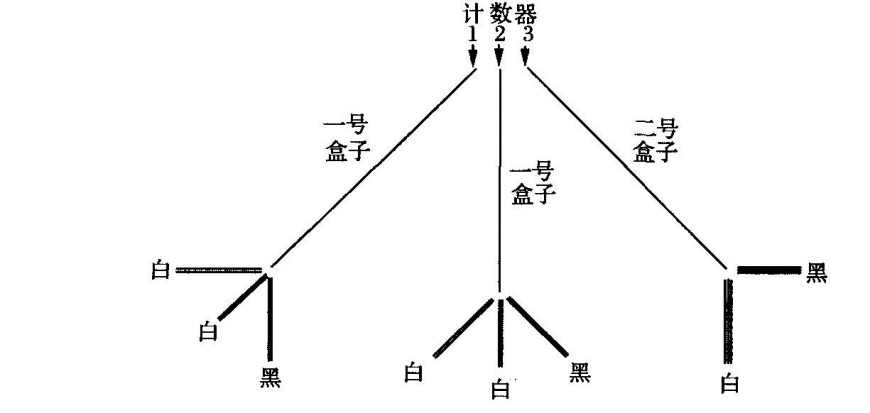
或者也可以表述为如下断言:这个图表“等价”于第二个图表。
现在我们可以将雅妮娜·霍西亚松的观点表述如下:
在第一种对策中我们本质上有九个相等的可能性。(正如图表明确表明的,我们也可以不用任何袋子,并且用两个不同的盒子都标上“一号”,来代替原来的那只一号盒子,这样的话三个盒子里一共有九个球,其中五个是白色的。)我们可以这样表述我们的结果:首先我们数出完成游戏的所有相等方式或相等可能性(共有9种),然后再数出抽中一个白球的可能性的数量(结果为5)。那么比例![]() 就是答案。
就是答案。
但这个方法并不适用于第二种对策。其结果是![]() ,但如果说我们有18种可能性,而其中11种是有利的,那么这种说法显然不是真的:任何可能性的计数都无法产生此结果。虽然第二种对策也很简单(在计算过程中没有丝毫困难之处),虽然它在每一步骤中都是等概率或等可能性的,但计数(相等的)可能性的理论却无法得出其结果。它包含某种“18种等概率”的假想构造,我们无疑可以计算[calculate]出这些等概率,但它们在第二种对策中绝对不是真实存在的。因为即便第三个图表描述的对策“等价”于第二个对策——任何对概率计算略有所知的人都能一眼看出这一点——但实际上它描述的是一个新的对策,完全不同于第二种。而这第二种对策(有8种不相等的可能性)和第三种对策(有18种相等的可能性)之间的“等价”,我们既无法先于计算构造而“看出”它,也无法将之“假定”为计算的基础。
,但如果说我们有18种可能性,而其中11种是有利的,那么这种说法显然不是真的:任何可能性的计数都无法产生此结果。虽然第二种对策也很简单(在计算过程中没有丝毫困难之处),虽然它在每一步骤中都是等概率或等可能性的,但计数(相等的)可能性的理论却无法得出其结果。它包含某种“18种等概率”的假想构造,我们无疑可以计算[calculate]出这些等概率,但它们在第二种对策中绝对不是真实存在的。因为即便第三个图表描述的对策“等价”于第二个对策——任何对概率计算略有所知的人都能一眼看出这一点——但实际上它描述的是一个新的对策,完全不同于第二种。而这第二种对策(有8种不相等的可能性)和第三种对策(有18种相等的可能性)之间的“等价”,我们既无法先于计算构造而“看出”它,也无法将之“假定”为计算的基础。
总结一下上面的论证。在第二种对策中,有8种不同取球方式,其中5种能取出白球。但这些可能性是不相等的(无论原因为何),并且是计算的结果告诉了我们答案为![]() ,而不是据称相等的可能性计数告诉了我们这一点。换言之,虽然问题是依据相等的可能性的存在来加以表述的,但其结果——虽然非常简单——却不能用这种方式来表述。这表明基于相等的可能性计数的任何定义都是不适当的。
,而不是据称相等的可能性计数告诉了我们这一点。换言之,虽然问题是依据相等的可能性的存在来加以表述的,但其结果——虽然非常简单——却不能用这种方式来表述。这表明基于相等的可能性计数的任何定义都是不适当的。
(c)在新经典理论中,表明了某些集具有0测度(或1测度)的定理代替了具有一定重要性的极限定理,这一代替有着哲学上的重要意义。一方面它解决了概率理论中某些据称的悖论,另一方面它帮助我们搭建了一座连接概率假说与依据相对频率的检验的“桥梁”。
最近这些据称的悖论成了人们讨论的热点。[31]它们与有时被称为“库尔诺[Cournot]原理”(或“库尔诺引理”)的东西有关。这个原理可以表述为“概率很小的事件实际上不可能”。[32]这个原理(以及任何类似的原理)问题就在于,事实上那些概率很小的事件确实发生了,哪怕非常罕见。用保罗·伯尔内[Paul Bernays]的话来说:“我们无疑能构造出库尔诺引理的反例(例如我中了彩票头奖)。”[33](此外,所有充分复杂的实际出现其概率都非常之低。)
在概率理论中这个问题呈现为两种非常不同的形式。第一,它呈现为桥梁问题——从概率到频率的转换;第二,它呈现于频率理论之中(呈现为概率陈述的可检验性问题,我在《逻辑》中对此有详细讨论)。
上述第一个形式问题完全可以通过由新经典理论推导出来的新频率理论解决。也就是说,通过推导出来的强大数律以及杜布作为“几乎确定的”赌博系统的无用性定理来解决。
因为这些结论的推导过程的概率精确地等于1;因此例外的概率精确地等于0,而非接近于0。准库尔诺原理涉及的是等于0的概率,不可能存在关于它的经验反例:不可能有中奖概率等于0的头奖彩票。
诚然,不可能存在反例这个情况,和下述事实有很大关系:新推导出来的理论和零概率涉及的是无穷序列,而我们不可能产生一个经验事实的无穷序列,我们也不可能用无穷数量的彩票去赌一次头奖。然而,无穷序列的收敛定律和随机性定律构成了频率理论的基础;在其推导中,所有的差别都来自我们要避免仅仅接近于1或接近于0的概率。
如果我们还记得冯·米泽斯对这个“桥梁”的批判,我们就能清楚地认识到这一点。[34]他指出,为了使用伯努利定理或普瓦松定理来证明从经典概率陈述到频率陈述的还原过程,我们必须先验假定这样的辅助原则:“一旦我们通过计算得到只比1小一点的概率,那么这个事件在实验的几乎所有重复中都会发生。”但冯·米泽斯也指出,如果我们将0.999这个概率诠释为“几乎总是”,那么就必须“立刻承认0.50这个概率意味着在100次情形中平均有50次会发生这个事件”。换言之,这就等同于立刻采用了频率定义。
但新推导出来的理论在此有所不同。
首先,它解决了下述难题:将0.999这个概率诠释为意味着“几乎总是”,这为什么不能令人满意?无论多么接近1,总需要一个等于0.999的频率极限之类的东西,也总需要“0.999这个概率对赌博系统不敏感”这个陈述。换言之,如果我们打算在频率的意义上诠释0.999,我们就需要整个频率理论。但如果我们得到了一个精确地等于1(或等于0,这是零测度的情形)的概率,情况就不同了。当然,即使在这一情况下,“概率”也必定意味着某些与频率有关的东西,如果我们希望得到需要的结果的话。但我们不再需要确保任何精确的关联——例如极限公理和随机性公理;因为显然它们是无效的,除非概率(测度)为零,但这样的话我们就可以忽略之。因此我们需要确保的仅仅是,在随机事件的情形中,零概率(或零测度)意味着作为非概然性而可以忽略不计的概率。
其次,如果我们希望以这种方式诠释“概率”,那么我们必定要承认0.50这个概率意味着100次情形中发生50次的概率为1。现在我们可以证明这个结论成立,但我们并不需要在证明中假定某种频率定义。因此频率定义是不充分的,这并不构成什么问题。实际上它根本就是不必要的:即便不假定概率意味着某种频率极限,我们也可以推导出与频率极限相关的种种结论;因此我们可以做到赋予“概率”某种更广泛的、更模糊的意义,而在这过程中却不会威胁到那座桥梁的安全——这桥梁的一边是概率陈述,而另一边则连着服从于统计检验的频率陈述。
无论如何,只有客观地诠释经典理论——例如在趋向性诠释的意义上——我们才能建造这座连接经典理论和统计学的“桥梁”。至于主观诠释,我以前作出的那些批判是适用的。(见《逻辑》第48节注释6,和第62节注释3。)
(d)我们已经知道,新经典理论并不定义“概率”,因此也不打算像经典理论和冯·米泽斯理论那样,从“概率”定义中推导出计算方法。相反,它首先构造的就是计算方法(或者是依据某种公理学方式,或者是将之作为测度论的一部分)。随后引入的就是种种关于此计算的诠释,例如主观的或客观的。但主观诠释在独立性理论中是失败的,这促使我们必须采用趋向性诠释。
然而,严格意义上的冯·米泽斯式的频率诠释(虽然我曾说过它是一致的,也是高度令人满意的)却无法支持新经典理论的可能诠释:新经典理论确实更为普适,它蕴涵了频率理论,并将之视为某种“首次逼近”。
因为除了频率诠释和趋向性诠释之外似乎不再有什么客观诠释,也因为频率诠释本身不可能成为“桥梁”,所以我认为唯一能够诠释(新)经典理论的就是趋向性诠释了。
这关联中的要点在于,这个新的理论确实能够赋予单称事件以概率。[35]虽然它考虑了事件的序列以及在这些序列中的频率,但是,在序列的某些被观察的节段中,一个事件的概率与其频率可能极为不同。(它仅仅符合几乎所有序列的频率极限。)
上文我试图说明冯·米泽斯类型的理论不可能诠释新经典(集合论的)概率理论的形式表述。[36]但乍看之下,似乎我们有可能调和这两种研究方法——即新经典方法和频率方法。因为有人会提出,下述关于新经典理论的频率诠释有可能实现冯·米泽斯之类频率理论家的主要目的:
(*)我们将新经典理论中所用的表述“事件x的概率(或测度)”诠释为意味着“在无穷序列集(随机或似随机)的几乎一切序列中,x类事件的频率极限”。
显然,只要给定某一概率分布(或场或标定空间),诠释(*)总是可用的。它来自于强大数律和杜布定理。但下面我将表明,(*)极度令人不满意:它实际上是本末倒置了,另外它还使问题情境变得更为模糊。
这个诠释(*)显然不等同于频率理论,但在内涵上二者是接近的:频率理论家应当会乐于将它视为某种推广,他们会提出下述论证来支持(*)。
在第一个实例中,“概率”意味着有限事件类中的相对频率,而在第二个实例中,它意味着无穷事件序列中相对频率的极限。在涉及无穷序列时,我们可以谈论“分布”,也即总和为1的种种基本概率,这个总和就是事件基本特性或类型的频率极限。而我们总有理由将分布视为相对于序列的类的——这些序列在名义上具有相同的给定分布——而非将其视为相对于一个序列的(这是冯·米泽斯之类频率理论家的看法)。这在本质上并没有改变下述频率学说:概率和分布仅在相对于一给定参考序列时才有意义。在这些新的形式中,它们在相对于所有那些属于某个参考序列集的参考序列时都有意义。这个集可以被称为“参考集”。最后我们甚至可以扩展这个参考序列的“参考集”,使之包括其频率与概率不相同的“例外序列”,假定这个参考集的测度为1,而且例外序列集的测度为0。这样一来,从频率理论的观点而言,我们就会发现(*)是关于概率计算的一个完美的自然诠释。
但我认为这个论证完全混淆了问题的情境。
因为我们只能在相对于一个基本分布,或称场、或称“空间”的意义上,谈论新经典理论意义上的概率或测度。如果没有建立这个分布,我们根本无法谈论任何序列集的测度。但这个分布是一个概率分布。因此,我们以某些特定的概率作为出发点,建立我们的测度系统,这是其他概率的系统。(正如冯·米泽斯自己一直强调的,概率是给定的,我们从它们中推导出其他东西。)所以“参考集”具有测度1,而“例外集”具有测度0,而这仅仅相对于我们的初始分布,也就是说,相对于在出发点时给定的概率;如果用一个测度1的序列集来说明概率,那么就是本末倒置了,因为换个初始分布(即在不同的空间形成的排列)集的测度也许会变成0。换言之,如果给定了所有可能的交错序列的连续集,那么对于一个初始分布来说,具有相应频率的交错序列的子集A其测度为1,而根据另一个分布,子集A的测度为0。[37]因此我们不可能用(*)来解释(或定义)“几乎所有序列的频率”这个意义上的“概率”。因为“几乎所有”翻译过来就是“测度0”,原本与分布相关,也就是说,与假定的初始概率相关。因此(*)确实是提供了一个可能的诠释,但它不能令人满意。
