第三章　关于概率的客观理论的评注

在本章中，我打算解释概率的趋向性诠释以及通常所谓“测度论方法”［measure-theoretical approah］如何能够取代频率诠释。我将试图表明，虽然这种方法可以取代频率理论，但它也必须借助于某种算后检查［post mortem］性质的证明，因为从测度论方法中，我们将“几乎可以演绎得出”频率理论。也就是说，测度论方法可以表明，我们偶然获得了某一违背冯·米泽斯的频率理论要求的随机序列，它的概率为零。换言之，“几乎可以确定”这些要求都将得到满足。[1]

这个新方法的重要性在于，测度论概率陈述都是单称概率陈述：都是断言“单称概率”的陈述。但是，从物理学角度看，“几乎蕴涵”一个频率的那种单称概率最好被诠释为物理趋向性。因此我认为，从频率理论向测度论的数学转换，对应着客观物理概率方面，由统计诠释向趋向性诠释的转换。

在本章开始我打算详细地解释趋向性诠释并说明采纳它的理由。而本章的主体部分是对概率的频率理论自1934年以来历史发展的评注。概率的频率理论在《逻辑》中扮演了重要角色，它尤其与冯·米泽斯理论的一致性问题有关。[2]1935年A·瓦尔德［A.Wald］加强了A.H·科普兰和我的种种假定（我曾试图将之减至最少），他首先成功证明了一个理论的一致性，该理论和冯·米泽斯的理论近似地强。A·丘奇［A.Church］进一步加强了瓦尔德的理论，他于1940年证明，对任何能有效计算的赌博系统（或赌博系统集）的选择不敏感的C类集合是一致的或非空的。[3]在我看来这些理论进展非常重要，因为它证明一个非常令人满意的频率理论本身能够成立，我们不必非得采用测度论方法才能得到此结果，尽管我们可以贪图其优点而自由选择是否采用它。此外很有价值的一点就是，甚至在无限序列中我们也可以谈论频率，而不用担心会出现不一致；因为对我们来说频率预测——从趋向性假说中“几乎可以推出”它们——依然是非常重要的：我们只有借助频率预测才能去检验这些假说。

20　趋向性的适用情形

在诠释特定的赌博情境时概率的主观诠释也有可能站得住脚，例如赌马。赌马中事件的客观条件是不良定义的，也是不可再现的。（但是，我确实不认为主观诠释可以应用于像这样的情况：我们可以构造一个强的情境——如果值得这么做的话——其中赌徒或“理性的打赌者”在打赌时想知道的是事件的客观条件、客观趋向性和客观赔率。于是下注者急于知道的是关于赛马的更多信息，而不是他自己的信念状态或他所掌握信息的逻辑强度。）然而在典型的机会游戏——例如轮盘赌、投掷骰子或抛掷硬币中，同时在一切物理实验中，主观诠释都完全失败了。因为在所有这些情形中概率都取决于实验的客观条件。

在《逻辑》中我考虑的仅仅是一种概率的客观诠释——纯粹统计的或频率诠释。（我认为这两个术语是同义词。）在那本书中，我一一驳斥了一般针对它的种种批评，通过这种方法试图重建这种诠释。在这里我想说，还存在第二种客观诠释，也是更好的一种诠释——趋向性诠释。我提出这个建议并不是因为有什么针对频率理论的批判得到证明。相反，我坚信频率理论是一致的，同时相信它能在实际中应用。但我也相信趋向性诠释具有决定性的优势。我将在本节中给出我的一些理由，而将另一些理由留至后文另行阐述。

在本节我的讨论将仅限于诠释“单称事件”（或事例［occurrence］）的概率这个问题，而当我在这里谈论与趋向性诠释相对的“概率的频率诠释”时，我指的是单称事件的概率的频率理论。

我们应该记得，从概率的频率诠释的观点来看，一个特定事件——例如投掷某个特定的骰子而获得六点——的概率正是此种事件在某一极长（可能是无穷长）事件序列中的相对频率。如果我们谈论的是一个单称事件（在《逻辑》第23节的意义上此即“事例”；另外参见第71节）的概率，例如这粒骰子在今天早上九点钟之后的第三次投掷中获得六点的概率，那么根据纯粹统计诠释，我们的意思是只有这第三次投掷应当被视为投掷序列中的成员，而因其能够成为这个序列的一员，所以它也拥有此序列的概率；也就是说，仅仅是作为此序列的相对频率的概率。

在本节中我将用论证来反驳这种诠释，并支持趋向性诠释，为了做到这一点我将使用上一章中得到的结果，即客观实验条件在概率诠释中的重要性。我的步骤是这样的：（1）我将首先表明，若从频率诠释的角度来思考，人们必定会有许多反对意见来驳斥趋向性诠释，并将之视为不可接受的。（2）随后我将概要性地回应这些反对意见。（3）然后我将提出频率诠释必定会遇到的一个难题，虽然这个难题乍看上去并不太严重。（4）最后我将指出，为了克服这个难题，我们必须要对频率诠释加以修正，这个修正初看上去很轻微，可采纳了这个表面上看似微不足道的修正，就等于采纳了趋向性诠释。

（1）从纯粹概率统计诠释的立场来看，趋向性诠释显然不可接受。因为“趋向性”可以被解释为概率（或可能性的测度或“权重”），而概率具有自我实现的倾向，它在长序列重复实验中的实际实现也关系到统计频率。因此引入趋向性是为了帮助我们说明或预测特定序列的统计特性，这也是趋向性的唯一功能。因此（坚持频率理论的理论家们会断言）它不允许我们去预测或谈论单称事件的任何性质，除非单称事件在同样条件下的重复能够产生具有特定统计特性的序列。这表明了趋向性诠释给频率诠释增加的不过是一个新词汇——“趋向性”——以及一个与之相关联的图景或隐喻——即某种倾向、意向或趋向。但这种拟人论的或心理学的隐喻甚至还没有“力”或“能量”这些旧的心理学隐喻有用，虽然后者要成为有用的物理学概念也必须褪除自身原来形而上学的或拟人论的意义。

粗略而言，这就是频率理论家们的观点。下面我将为趋向性诠释做辩护，我将使用两个不同的论证：其中（2）是初步的回应，而（3）和（4）将是我用来扭转局面的主要论述。

（2）作为初步的回应，我打算接受如下观点：趋向性观念与力的观念，尤其是力场的观念之间存在着某种类似。虽然“力”或“趋向性”这样的称谓都有可能是心理学的或拟人的隐喻，但这两个观念间的类似并不在于这一点，而更多地在于：这两个观念关注的都是物理世界的种种不可观察的意向特性，因此它们将有助于我们诠释物理理论。它们的用处在这儿。力的概念——尤其是力场的概念——引入了一种意向性物理实体，它是被某些方程式（而非隐喻）所描述的，为的是解释可观察的加速度。与此相似，趋向性概念，或趋向场的概念，引入了单称物理实验安排，也即单称物理事件的某种意向特性，为的是解释这些事件的重复序列的可观察频率。在这两个情形中，新观念的引入都因其对物理理论的有用而变得合法。在贝克莱的意义上这两个概念都是“超自然的”或“仅仅是词语而已”。但这些概念之所以有用的部分原因正在于，它们暗示理论关注的是某种不可观察的物理实体的特性，我们能够观察的仅仅是这个实体的某些非常表面的效应，而借助这些效应我们才有可能检验此理论。（见上文第11到15节。）支持趋向性诠释的主要论据在于，它能够消除量子论中某些非理性和主观主义的扰动因素——这些因素比趋向性更“形而上学”，而且这是负面意义上的“形而上学”。我们在评价趋向性诠释时，应该考虑的是它在这个应用领域中能否取得成功。[4]

以上就是初步的回应，下面我将论述支持趋向性诠释的主要论点。上文已经提到，在此步骤中我将指出频率诠释必须面对的特定难题。

（3）已有许多反对意见指向概率的频率诠释，特别是它与事件的无穷序列的观念，以及与相对频率的极限概念的关系。但在这里我不打算涉及这些反对意见，它们将留待下节讨论。（它们整体上无效。[5]）但据我所知，我下面将提出的一个很简单而又很重要的反驳以前还没人提过。

假定我们有一粒灌铅的骰子，在经过长实验序列后，我们发现了一个令人满意的结论：这粒灌了铅的骰子得到六点的概率非常接近于¼。现在让我们考虑一个序列b，它既包括这粒灌铅骰子的许多次投掷，也包括另一粒同质的、对称的骰子的几次（例如两三次）投掷。那么显然，在涉及这粒“公平的”骰子的那几次投掷时，我们必须说获得六点的概率是⅙而非¼，但问题是根据我们的假定，这几次投掷也属于某一序列的成员，而此投掷序列的统计频率是¼，另一方面，两三次投掷又不可能影响长序列的频率为¼。

我认为这个简单的异议是决定性的，虽然可能对其进行各种反驳。

下面将给出其中一种反驳，但我仅打算略述一二，因为它相当于退守到了概率的主观主义诠释的立场上。它等同于断言，正是我们关于这粒公平骰子的几次投掷的特殊知识、特殊信息改变了概率。根据我对主观理论的一贯立场，不需明说读者也该知道，我认为这种观点是不成立的。此外，我们现在讨论的这个例子还提供了另一种论证（虽然不是非常重要）来反对主观理论。虽然我们知道有两三次投掷是用正常骰子作出的，但我们却不一定知道具体是哪几次投掷。在此情形中，我们有足够充分的理由打赌（只要我们要赌的这个序列有充分的长度）此概率非常接近于¼，哪怕我们知道存在着两三次投掷，要是能识别出它们的话我们就不会赌这个数值。我们知道在这几次投掷的情形中六点的概率小于¼——实际上是⅙；但我们也知道我们无法识别出这几次投掷，而且如果赌的次数很多的话它们的影响必定很小。现在显然的是，即便我们仍然会赋予这些未知的投掷以⅙的概率，但这里的“概率”并不意味着——也不可能意味着——“依据我们的总体实际知识得出的合理赌注”（但主观理论就是这么认为的）。

现在让我们离开主观理论，看看频率理论将如何回应这个异议。

在许多年中我自己就是一个坚持频率理论的人，因此我很明白我自己的回应将是这样。

根据上文对序列b的描述，我们知道b是一个混合投掷序列，其中包括灌铅骰子的投掷以及（例如）三次公平骰子的投掷。我们估计或猜想（基于先前的经验或直觉——猜想的“基础”是什么倒无关紧要），灌铅骰子的投掷序列中出现六点的频率是¼，而在公平骰子的投掷序列中则是⅙。将后一种序列，即公平骰子的序列表示为“c”。那么b的结构的信息告诉我们：（ⅰ）p（a，b）=¼，或非常接近此值，因为几乎所有投掷都是灌铅骰子作出的；（ⅱ）bc——即同时属于b和c的三次投掷的类——是非空的；而因为bc包含着属于c的投掷，所以我们有资格断言，在属于bc的那些投掷中，六点的单称概率等于⅙——理由是这些单称投掷都是某一序列的成员，而对于此序列我们有p（a，c）=⅙。

粗略地说，这曾经就是我的回应；但我现在认为它显然完全无法令人满意，我甚至在想，当时我怎么会满足于这样的解答。

当然，下面这两个等式

是完全相容的（在无穷序列也是如此）。另外，毫无疑问，这两个情形也能在频率理论中得到实现：我们有可能构造某个序列b满足等式（ⅰ），同时选取一个序列bc——这是一个极长的、无穷的虚拟序列，其元素同时属于b和c——满足等式（ⅱ）。但我们的上述例子并不属于此种情况。因为在我们的例子中bc不是无穷的虚拟序列。根据我们的假定，它只包含三个元素。在bc中六点出现的情况只能是无、一次、两次或三次。但它在序列bc中肯定不可能出现⅙的频率，因为我们知道这个序列至多包含三个元素。

因此在我们的例子中只有两个无穷的或极长的序列：一个是（实际［actual］）序列b，另一个是（虚拟［virtual］）序列c。我们要考察的那类投掷都属于二者。而我们的问题是这样的。虽然投掷都属于这两个序列，虽然我们只知道那些特别的投掷bc发生于b中的某处（我们不知道具体在何处，因此也无法识别出它们），但我们却坚信无论如何在这些特别的情形中正确的、真的单称概率是⅙而非¼。或换言之，虽然它们属于这两个序列，但我们却肯定知道，它们单称概率的估计值等于序列c的频率而非b的——这正是因为它们对应的是另一粒不同的（公平的）骰子，也因为我们的估计或猜想是，在公平骰子的投掷序列中，有⅙的情形会出现六点。

（4）所有这些都表明频率理论家们必须要对这个理论做一定的修正——当然是很细微的修正。现在他们得说，事件的容许序列（参考序列、“集合”）必须是一个重复条件的序列。或更一般地，他们得说，容许序列必须是由生成条件集刻划的虚拟的或实际的序列，此条件集的重复实现产生了一个独立序列中的种种元素。

如果这样来做修正，我们的问题就立刻得到了解决。因为序列b就不再是容许参考序列了。它的一部分，也即包含灌铅骰子的投掷部分（即b）将产生一个容许序列，对于这个部分我们完全可以处理。剩余的部分bc包含的是常规骰子的投掷，属于此类投掷的虚拟序列c——这也是一个容许序列。这一部分也毫无问题。显然，一旦采纳了这个修正，频率诠释就不再有任何难题了。

此外，我在这里给出的“修正”所阐述的，本身就是大多数频率理论家（包括我）一直都遵循的一个假说；这个修正不过是将之明确表达出来罢了。

但是，如果我们仔细考察这个表面上非常轻微的修正，我们就会发现它等同于从频率诠释到趋向性诠释的转换。

频率诠释总认为概率是相对于某一“给定”序列的；它有着下述假定：概率是某一给定序列的特性。但根据我们的修正，序列本身被定义为它生成条件的集合；这样一来，我们就可以说概率是生成条件的特性。

但这其中有着极大的差别，尤其对单称事件（或“事例”）的概率来说更是如此。因为现在我们可以说，单称事件a具有概率p（a，b）是因为它是根据生成条件b而产生的一个事件，而非因为它是序列b中的成员。这样的话，单称事件哪怕只出现一次，它也有可能具有某一概率；因为它的概率是其生成条件的特性：是生成条件产生出了它。

诚然，对于上述观点频率理论家们也会有不同意见：即使概率是生成条件的特性，但它也等于这些条件所生成的虚拟序列或实际序列之中的相对频率。然而，如果我们仔细考察这个想法的话就会发现，这样一来频率理论家们显然就已经是站在趋向性诠释的立场上了——尽管是不经意地。因为，如果概率是生成条件（例如实验组织）的特性，而且如果我们因此认为它取决于这些条件，那么频率理论家的上述异议就暗示着虚拟频率必定也取决于这些条件。但这意味着我们必须去实现这些条件，将它们视为蕴涵着某种倾向、意向或趋向性去产生其频率等于此概率的序列；而这些正是趋向性理论断言的内容。

有人会认为，只要我们用纯粹的可能性来代替趋向性，我们就可以避免这最后一步——将趋向性归因于生成条件。他们希望用这种方式来避免趋向性诠释中可能是最遭人非议的方面：它在直觉上带有类似于“生命力”这样的拟人论色彩，许多人常常根据这一点而将之称为空洞的伪解释。

用可能性来诠释概率，这是一个很古老的思想了。概率的经典诠释之一依据的就是相等的可能性，例如依据所有可能性的数量来划分出有利的可能性数量；对于这种诠释也存在着众所周知的反对（例如灌铅骰子的情形所表明的），出于论证的考虑，我们不准备讨论这个反对意见；同时，我们的讨论还将仅限于对称的骰子或硬币之类的情形中，这是为了在可能性定义和趋向性诠释之间做比较。

这两种诠释的共同点相当多。二者的首要关注都是单称事件，以及每个事件发生条件中固有的可能性。二者都认为这些条件在原则上可再现，因此它们能够产生事件序列。二者之间的差别似乎仅在于下述情形：趋向性诠释引入了那种遭人非议的形而上学趋向性，而可能性诠释则简单地归之于条件的物理对称性——归之于留待条件来加以说明的那些相等的可能性。

但这些共同点都是表面上的。要费一番力气才能看出，纯粹的可能性无法满足我们的目的，也无法满足物理学家或赌徒的目的；甚至这个经典定义也隐含地假定了，相等的可能性必定依附着实现这些可能性的相等的意向、倾向或趋向性。

如果我们首先考虑非常接近于零的等可能性［equi-possibilities］，就很容易看到这一点。非常接近于零的等可能性的一个例子就是任意长度为n的有限0和1序列的概率：这种序列有2n个，因此在等可能性的情形中，每一个序列的可能性都为1/2n，对于较大的n这非常接近于零。而互补可能性则接近于一。一般我们会将这些接近于零的可能性诠释为“几乎不可能的”，或“几乎不可能实现自身的”，而接近于一的互补概率则被诠释为“几乎必然的”，或“几乎总可能实现自身的”。

但是，如果我们认为接近于零的可能性和接近于一的可能性都可以被诠释为预测——“几乎不会发生”和“几乎总会发生”——那么我们就会很容易明白，假定抛掷硬币获得正面或反面的两种可能性是穷尽的、排他的和相等的，那么它们也可以被诠释为预测。它们对应于预测“在长序列的大约一半情形中几乎能确定地实现自身”。因为根据伯努利定理（以及上文长度为n的序列的例子），我们知道在这种诠释看来，½的可能性逻辑上等价于上文关于接近于零或一的可能性的诠释。

换一种稍微不同的方式来说明这一点：纯粹的可能性无法产生任何预测。例如，明天将有一场地震（仅仅）摧毁南北十三度纬线之间的所有房子，这是可能的。没有人能计算出这个可能性，但在大多数人的估计中它是极小的；像这样纯粹的可能性不产生任何预测，但“它是极小的”这个估计有可能产生下述预测：这一事件（“在所有概率上”）不会发生。

因此，关于可能性测度的估计——即关于附属于它的概率估计——总有着预测的性质，但是，如果仅仅说某一事件是可能的，那么我们就不可能预测这个事件。换言之，我们不假定像这样的可能性有任何实现自身的倾向；但我们在诠释附属于此可能性的概率测度或“权重”时，确实认为这是在测度其实现自身的意向、倾向或趋向性；而在物理学（或打赌中），我们关注的就是这种可能性的测度或“权重”，并认为它有资格作出预测。因此不可避免地，我们会认为可能性测度就是意向、倾向或趋向性。我选择“趋向性诠释”这个名称的理由就是我希望强调，我们常常都忽略了上述理论——概率理论的发展历史也表明了这一点。

因此我并不担心人们说什么趋向性是拟人论的概念，或说它类似于生命力的概念等等。（这个概念确实空洞，我也不大喜欢它。但大多数有机体都有为生存而斗争的意向、倾向或趋向，这并不是一个空洞的概念，反而非常有用；而之所以说生命力这个概念空洞，恐怕是因为它本来打算说明下述断言，但又未能完成目标：大多数有机体都有一种为生存而斗争的趋向，在此过程中还产生了其他种种趋向，例如探索周遭环境和占据新的生态位趋向。）

总而言之，趋向性诠释坚持的是这样的观点，即概率都是长（实际或虚拟）序列中的猜想性或估计性统计频率。但是，因为我们将这些序列定义为它们元素的生成方式——即生产条件——所以我们必定要将猜想性概率附属到这些生成条件中：我们必定要承认，它们依赖这些条件，并会随之改变。对频率诠释的修正几乎不可避免地导致下述猜想：概率是这些条件的意向特性——也即趋向性。这允许我们将单称事件的概率诠释为单称事件本身的某种特性，而此特性的测度方法则是猜想性的潜在的或虚拟的统计频率，而非实际的或已观察到的频率。

像所有意向特性一样，趋向性在某些方面也类似于亚里士多德主义的潜力。但二者之间有着重大差别：和亚里士多德主义者所认为的不同，趋向性不可能为个体事物所固有。它们不是骰子、硬币的固有特性，而是某种更为抽象的东西，虽然本身在物理上是实在的：它们是总体客观情境的关系特性，它们是某种只依赖于我们猜想情境的隐藏特性。如果我们要检验我们的猜想，我们就必须在事件的每次重复中都保持某些条件的恒定性，以此来保持相关情境的恒定性。在此情形中趋向性又一次类似于力或力场：牛顿的力不是某一事物的特性，而是至少两个事物之间的关系特性；而在物理系统中实际上产生的力总是具有整个物理系统的特性。力和趋向性一样，都是关系概念。

我们往往会忽略趋向性的（例如一次实验组织中的）关系性质：我们会认为在半数硬币抛掷中出现正面或反面的趋向性是硬币的固有特性。但事实上，与其说这是硬币的特性，不如说这是硬币抛掷的特性。从这个事实来看，当我们将硬币抛向松软的沙土或泥土地面（这样的话它有可能会直立起来）而非水泥地面时，我们得到的概率就会变低；这表明甚至在这最简单的情形中我们也要考虑好几个实验条件。

回忆一下我们对“p（a，b）”中b——第二个论证——的角色分析结论，我们就会发现这个结论既支持上述观点，也被上述观点所支持。上述观点表明，即便我们将“b”诠释为事件（潜在或虚拟）序列的名字，但我们并不需要承认所有可能的序列：我们唯一需要承认的序列可以被描述为生成特定可能结果的情境重复，它们的特征就是其生成方法，也即实验条件集的生成。

但人们也有可能会误解我的论证，特别是误解本节中的这些观点。他们也许会将之视为某种意义分析的方法：似乎我已经做的或试图在做的事情就是在某种上下文中用“概率”这个词来表示趋向性。我甚至还一度鼓励了这种误解，特别是在前一节中，我提出频率理论部分地是一种错误的意义分析结果，或是一种不完备的意义分析结果。但我并没有打算用另一种意义分析来取代它。这一点很容易就能看出来，因为我的目的是提出一个与牛顿力的假说相类似的新的物理假说（也可能是形而上学假说）。这个假说的内容是，所有实验组织（因此也包括系统的所有状态）都能生成有时可用频率来加以检验的趋向性。这个假说是可检验的，它能被某些量子实验所验证。例如双孔实验（对照《后记》第三卷第18节）就可以说是概率的纯粹统计诠释和概率的趋向性诠释之间的一个关键实验，并能最终判定胜出者为趋向性诠释。

我将在本书的剩余部分详细地讨论趋向性诠释，我希望人们能根据这些讨论来判定趋向性诠释的理论价值。

在本章我将表明，从频率诠释到趋向性诠释的转换，对应从冯·米泽斯、科普兰、瓦尔德和丘奇（也包括我自己）发展出来的数学频率理论到对概率进行新经典的或测度论处理的转换，我认为后者要优于频率理论，不仅从哲学而言如此，而且从纯数学而言也是如此。《后记》第二卷末尾主要论述的是决定论问题，我试图在那里表明，一直阻碍人们自觉接受趋向性诠释的正是对形而上学决定论的信仰。在关于量子论的《后记》第三卷中我将检验趋向性诠释的实用性。在（第三卷）跋中我打算指出，我们可以根据趋向性理论来构造一种新的物理学形而上学——一种物理学新的研究纲领，它不仅统一了旧纲领，而且还将允许我们统一物理学和生物学。

21　频率理论的成功之处

无论我们用何种方式来诠释科学中的概率陈述，频率诠释都无疑具有根本的重要性，因为我们交付给经验检验的总是频率陈述。基于这个原因，我将首先讨论在《逻辑》中占据了较长篇幅（第7章）的一些问题。

当我写作《逻辑》中的第7章时，冯·米泽斯那所谓随机性（或赌博系统的无用性）公理或公设正成为人们关注的焦点。

卡尔·门格尔是这样论述那个局面的[6]：“就在那时，发生了第二个被证明对瓦尔德后来的工作和生活起到了关键作用的事件。维也纳哲学家卡尔·波普尔……试图明确随机序列的概念，并用此弥补冯·米泽斯集合定义中的种种显而易见的缺陷。我（在石里克的哲学小组中[7]）听到了关于波普尔概念的半技术性阐述，之后我请那个人在数学研讨会上详细讲解其中的所有要点。瓦尔德对此非常关注[8]，随后他得出了自己的结论，其结果就是他关于集合概念的自相一致性的高水准论文……刊载于《数学研讨会报告集》……这些关于集合以及时间序列……的研究是在摩根斯坦的[9]建议下进行的，正是经过这些研究工作之后，瓦尔德将注意力转向了统计学的基本理论。”[10]

我在此提及这件事情是有原因的，这件事对瓦尔德和我来说都很重要。因为瓦尔德的工作是对我工作的一个推广，无论在范围上还是在深度上都远远超出了我在此领域中预想的界限。（因此我从未就此论题再发表过任何论文，我在《逻辑》中指出了这一点。）粗略地说，瓦尔德用了一种“对角论证”的东西，这使我们可以构造出一些对赌博系统的任何可数集都不敏感的序列。

简言之，瓦尔德的结果是这样的：他表明，给定赌博系统的任何可数集，都存在一些集合——实际上是整个集合连续统——它们对所有这些赌博系统都不敏感（换言之，存在一些具有收敛频率的序列，它们是赌博系统无法影响到的）。他进而表明，如果这个赌博系统集是“依据结构方法来定义的”，那么我们就能有效地构造出一些集合实例，它们对所有这些赌博系统都不敏感。[11]

在阿隆索·丘奇的一篇论文中，他对瓦尔德的结果[12]做了最后修正。瓦尔德是在一个较为粗略的意义上使用“依据结构方法来定义”和“可以被有效地［effectively］构造”这两个术语的：他曾简单地断言，对于任意一个（可数的）赌博系统集，无论我们依据什么指示或方法构造出属于此集的所有系统，这种指示或方法都可被用来构造出一些从此集的所有赌博系统来看对选择不敏感的集合。

而丘奇指出[13]，在这种情形中我们可以应用有效可计算性［effective calculability］的概念，他曾在1936年提出了一个针对此概念的形式定义。他重新提到了冯·米泽斯，后者严厉批判了[14]所有像科普兰一样的人——他们研究那些有可能用某种规则加以构造的集合；[15]他还更严厉地批判了像我这样的人——我们曾给出过具体的构造方法。[16]对于这种序列，必定总会存在成功的赌博系统，这是因为这些序列可以通过数学构造而产生；冯·米泽斯指出，对于这些序列，总存在更成功的赌博系统。

在我看来，这从不构成对我的理论的真正反对。我想做的是推导出概率理论的形式表述，而我依据的是下述假定：序列第n个元素的概率独立于其所有前导的特性。但丘奇认为冯·米泽斯的反对意见很重要。他的回应是，任何能应用在实践中的选择系统（赌博系统）都应当能允许我们有效地计算出被选择的元素（为了能对它们进行“赌博”）。因此他提出下述定义随机序列的方法：不改变冯·米泽斯第一条件（“收敛公理”），而改变冯·米泽斯第二条件（“随机性公理”或“排除赌博系统公理”）以满足下述要求，即随机序列应当对所有有效可计算的选择函数不敏感。

丘奇用这种方法排除了所有有效可计算的——也即所有在实践中能应用的赌博系统（它们在数学上都是精确可表达的），在我看来他也就成功地精确刻划了冯·米泽斯所考虑的那类集合的性质。丘奇表明，在这个情形中也可以应用瓦尔德的证明。[17]因此我们就证明了集合——或丘奇所谓的“随机过程”——的存在。

在我看来，这些结论非常完备地证明了冯·米泽斯的频率理论，而这证明也是必要的。这些结论不仅堵住了所有批评者的嘴巴，而且也给所有反对“收敛公理”（或“极限公理”）的人（譬如我）一个满意的答案。

因为丘奇表明，波雷尔的一个最重要的结论[18]也可以扩展到丘奇的“随机序列”——至少可以扩展到具有两个特性“0”和“1”的随机序列，只要它们为等分布，即p（0）=p（1）=½。[19]

我记得丘奇的结论是这样的：如果我们考虑所有可能的有限“交错序列”——即所有可能的有限的0和1序列——那么在丘奇的意义上几乎所有这种序列都是随机序列。

这显然暗含了以下两点：第一，几乎所有交错序列在无穷延伸的情况下都是收敛的；第二，几乎所有这种序列都具有“似偶然的”或“随机的”性质。它还进一步暗含着这样的观点：这种随机序列是存在的。

在这里“几乎所有”的意思是：将0和1序列诠释为介于零和一之间实数的二进位分式展开式，我们将发现，那些不是随机的展开式，也即不满足丘奇两个随机性条件的展开式，构成了一个零测度集。

为了直观地理解这个定理，对于具有½概率的交错序列，我们可以考虑长度为2、4、6…的所有可能序列，并以长度排序。（考虑到本文的篇幅，我下面仅给出最初的两个集。）

长度2：序列数：4

00　　　　　　10

01　　　　　　11

长度4：序列数：16

0000　　　　　1000

0001　　　　　1001

0010　　　　　1010

0011　　　　　1011

0100　　　　　1100

0101　　　　　1101

0110　　　　　1110

0111　　　　　1111

一般情况下，长度为n的不同序列的数量为2n。

伯努利很早以前就发现了下述规律：

（1）完全等分布序列的相对频率随其长度的增长而减少。（对于长度为2的序列，其相对频率为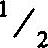；长度为4，相对频率为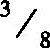；长度为6，相对频率为。）

（2）然而，几乎等分布序列的相对频率随其长度的增长而增加。（至少要写出长度为6的序列才能较为明显地看出这一点。）

（3）对于那些在直观上具有似随机性质、具有良好逼近的、对“正规序数选择”不敏感的序列，其相对频率随其程度的增长而增加。（要相当长的序列——至少6和8——才能较为明显地看出这一点。）

如果序列不断增长，大尺度上的比例将非常接近于p（0）=p（1）=½，而随着选择方法越来越多，大尺度上的比例也将变得越来越不敏感。这样一来就得到了我们的定理。

根据这个结论，现在让我们来考虑针对收敛公理的那种常见批判，它是这样的：

（a）假设某个无法依据数学规则来计算的序列是收敛的，这种假设毫无意义；

（b）根据概率理论，所有序列都是可能的，也是和任何概率假定相容的，因此这对于下述序列[20]

010011000000111111000000000000000000111111111111111111

也同样适用，此序列的频率在½和⅓之间振荡，因此不是收敛的。但是，因为这个发散序列显然是一个可能序列，因此不容许将它排除。

现在我可以给出对这个反对观点的回应：

（a）几乎所有依据数学规则不是有效可计算的序列都具有收敛的频率。

（b）虽然确实存在发散序列，但因为它们是发散序列，我们便可以忽略它们。这就使我们得出稍微有些理想化、简化的理论。

因此，“收敛公理”或（[21]冯·米泽斯所谓的“极限公理”）就完全摆脱了它那表面上遭人非议的性质。它不再是一个武断的假设，而是假定了一个具有理想化的、简化性质的定理。它不再适用于经验上非存在的无穷序列，而是仅仅理想化了某种特性，此特性为几乎所有极长的有限序列所共有，而且当序列的长度增加时，相当多的有限序列都拥有此特性。

这一切都非常直白，也非常令人满意；我要重申的是，在我看来，它完全证明了频率方法的正确性。

但正是这个对频率方法的证明取代了频率理论本身：恰在我们能从数学上完全证明频率理论的时刻起，频率理论就成为过时的东西了。因为证明了频率理论的那个理论本身在冯·米泽斯的意义上并非频率理论：它在本质上是一个测度可能性或可能性集的理论，就像经典理论一样（最初是来自于伯努利的工作）。它可以被称作“新经典”理论。因为它能证明频率理论，因此我们就认为它是更强的理论。实际上，它使得频率理论成为冗余。换言之，一旦实现了伯努利的目标，在经典理论或不如说新经典理论和频率理论之间的鸿沟上搭起一座桥梁，那么后者也就在这个证明过程中丧失了独立的存在性，而成为前者的一部分。

22　频率理论的失败之处

频率理论并不需要新经典理论：它完全是自足的。但它也有失败之处，那是因为它并不完全普适。一些极具价值和意义的问题及其解答并不涵盖在频率理论的体系内。

为了用例子来说明这一点，我将较为详细地讨论上一节提到的那个定理的简单形式，即在几乎所有交错序列中，1的相对频率具有极限。

令a是一个交错序列（即0和1序列）。令n'是a的第n个位置上1的总个数，那么n'/n就是a的第n个位置上1的相对频率。

用数学语言说，n'/n具有极限——称之为p（l，a）——当且仅当对于我们所选取的任意小的分数ε＞0，都存在一个数m，使得从第m个位置起，n'/n与p（1，a）的偏差小于ε。用符号来表示就是：

（*）存在某一m，使得对于所有满足n＞m的n，都有

但是，对于一个经验的随机交错序列a（对于一个集合），我们无法根据任何选取的ε有效计算出这个数字m（这是因为集合不是由数学规则决定的）。我们能做到的是：对于任何选取的ε，无论它多么小，如果（*）失败的概率小于ε，那么我们就可以有效计算出m；这等同于说，（*）成立的概率大于1-ε。实际上，有m等于1/ε3就足够了，如果ε是个很小的分数，那么这个数字将非常巨大。（如果ε=1/1，000，那么m=1，000，000，000，这意味着从交错序列的第1，000，000，000个位置起，相对频率与p（1，a）之间出现超过1/1，000偏差的概率小于1/1，000。）[22]

以此形式，冯·米泽斯表明[23]这个定理可以在频率理论中被如下诠释。

我们这样看待交错序列a及其所构成的新集合b：将a分割成许多长度为n的极长（非交叠）节段，其中n＞m。a的这些长节段成为新集合b的元素。而定理断言的是，在作为b的元素的这些节段中，平均而言，与p（1，a）的偏差超过1/1，000的情形在每1，000个节段中不会超过一次；因此在集合b中，这些偏差的相对频率将趋近于某一小于1/1，000的极限——无论我们选取的n有多大。

我认为不会再有人反对关于此定理的这种频率诠释。

但是，我们讨论的这个定理无法得出下述推论：几乎所有交错序列都具有收敛的频率。频率理论并不蕴涵从这个定理到此推论的推理。

在经典理论的框架内，对这个定理的诠释不会与频率诠释有太大差别。此诠释可以表述如下。（为方便讨论，在此我仅限于讨论等分布p（1）=½的情形。）

从长度n（这里选取的n须满足n＞m）的各种节段中，每一种挑出一个样本放入一个袋子，那么袋子里就有2n个节段，两两不相同。在这些节段中，在每个节段的第n个位置——即第1，000，000，000个位置——之后与½的偏差超过ε=的情形至多为。

在给定这个定理的这种表述之后，我们就可以推理出下述结论：

我们可以选取任意小的ε，如果我们让ε越来越小，那么由于m=1/ε3，所以m将趋近于无穷（因此n也趋近于无穷）。最后，即当ε→0，我们的袋子里包含的就不再是所有可能的具有某一有限长度n的节段集，而是所有可能的无穷序列集（顺带指出，正如康托尔的“对角论证”所表明的，它也是一个非可数集）。同时，找到一个非收敛序列的概率将等于零。

在冯·米泽斯用来表述定理的那种频率诠释中是不可能包含这个论证的。首先，他一开始就将一个交错序列a分割成数量无穷的长节段n。但我们不可能将a分割成无穷多的无穷长度的节段——甚至分割成两个这样的节段也不可能：无论以何种方式将a分割成几个节段，如果要求其中至少有一个是无穷的，这都至多只能产生a的一个无穷“节段”，即a自身（减去某一起始节段）。因此也不可能用这样的方法来构造b；但是，根据冯·米泽斯的定义，只有在b中才能找到（或找不到）偏差的概率。

其次，频率理论不可能接受其元素为无穷序列的集合b的概念。在频率理论中，集合的元素在本质上是可观察事件，或实验结果。它们也是事件的有限序列，因为有限序列本身可以被诠释为复合事件。但集合的元素显然不可能是事件的无穷序列。

因此冯·米泽斯的诠释实际上完全无法过渡到上述极限。在大多数情形中这并不产生什么麻烦：通常我们表述极限定理的内容时都不需要在实际中完成这个过渡，而只需引入越来越长的有限序列。甚至在上文的那个例子中情形也是如此，只要我们考虑的是定理的经典诠释——这正是因为它不允许我们达到这个极限。但在这个不允许我们达到这个极限的理论框架中，定理的理论力量就被削弱了，它没有在有可能完成这个过渡的框架中那么完备。

对于我的这个批判，频率理论家可能会有下述反对意见。他会说，他承认冯·米泽斯的诠释即便本身正确，也无法使定理拥有完备的力量。但是，通过将经典定理直接翻译为集合语言，这个缺陷是可以弥补的。对应于我装满了2n个节段（其中n＞m=1/ε3[24]）的袋子，存在着一个集合b，它里面是一些从我的袋子中随机抽取的节段。从这个袋子里抽取一个节段而其与½的偏差超过ε的概率——即相对频率的极限——将小于ε，这正如经典模型中的情形一样。此外，如果m趋近于无穷，因而n也趋近于无穷，那么这个概率将为零。

我相信我能反驳这个异议，但首先得仔细分析它。它正确地表明，概率应当永远联系着一个非常灵活多变的频率观念：这个观念不仅包括有限类中的频率，也包括它的推广，即无穷序列中的频率极限，以及更进一步的推广，例如针对连续集而定义的测度。但冯·米泽斯的频率理论仅仅承认可观察事件的无穷序列中的频率极限。考虑到这一点，我们有下述见解：

（a）我的假想对手们提出要重新诠释有限类中的相对频率，方法则是从那种有限类中构造出随机抽取集合；如果我们接受此方法，那么这种重新诠释就是平凡和冗余的。因为它仅仅是用比例的无穷序列的极限代替了日常的有限比例；此外，它还假定了“随机”抽取。

（b）我们的那个袋子及其频率都没有任何的似偶然性。这是纯粹的数学模型，对于任何n，所有频率都精确可计算。至于将这些同样的频率诠释为似偶然抽取或随机（即独立）抽取的结果，这和我们的原初设想根本没关系。

（c）在冯·米泽斯形式的频率理论中，陈述“随机抽取将产生这些频率”必须一直维持其性质，即它是有关随机事件频率的假说性估计。但有关袋子内容的相应陈述都是可证明的数学定理。

（d）因此陈述“从一个装满可能的0和1序列的袋子中抽取具有非收敛频率的序列，其概率等于零”（这个）肯定不等价于我们上文讨论的定理，因为几乎所有此类序列都是收敛的（非收敛的序列的测度集等于零）。

这样一来情形就很明显了：我们讨论的那个定理——“强大数律”的某种形式——并不等同于冯·米泽斯“收敛公理”的某种推论。它并不（也不可能）确立所有序列都是收敛的，而只能确立几乎所有序列都是收敛的。“收敛公理”刻划的是那些包含着收敛序列的“集合”性质。换言之，冯·米泽斯的理论非常正确地挑选出了一种特别的序列类。

冯·米泽斯第二公理，即随机性公理的情形与此非常类似。它也无法推导出这些结果。但我们可以用杜布的定理来取代它：假定与论题相关的那些序列包含的是独立事件，那么在几乎所有序列中（在所有独立事件序列中，例外情形就是零测度集）任何赌博系统都将失败。

实际上，这里采用的这个独立性假定完全等同于我的假定：第n个元素独立于其所有前导，或对于前导选择是n-1-不敏感的；在这个意义上，我的做法——单独将独立性或n-不敏感性假定作为理论的基础（抛弃收敛公理）——大体而言就是正确的。就独立性或n-不敏感性具有明显直观意义而言，这是重要的。而事实确实如此：我们在投掷骰子之前都要充分晃动它们或混合它们，这是因为我们都希望确保先前的投掷或抽取结果不会对第n次投掷或抽取结果产生任何影响。

23　失败的意义

接着刚刚的讨论，我们已经来到了关键点上。频率理论的这种失败有着非常重大的理论意义。

新经典理论完全可以解决我在《逻辑》第49节中提到的“机遇理论的基本问题”。这个理论和趋向性诠释相结合，就能解释为何独立事件（这些事件对前导选择是n-不敏感的）序列的行为如此奇怪；为何它们的行为和冯·米泽斯的集合相同；为何它们的频率呈现出收敛的倾向；为何它们同时又是似随机的，以至于（几乎）所有赌博系统都失败了。这种奇怪的行为，这种规律性cum［连同］非规律性，从某一方面而言虽然是我们期望机遇事件应当具有的，但认真思考下去的话，却会发现种种难解之处——若是认识到这一点，我们就能解决这个机遇理论的基本问题。

新经典理论和趋向性诠释一起向我们表明，在独立或似机遇的系统的无穷序列中，对独立事件序列这种行为的期望概率应当等于1。

这个问题的解决基本上依靠的是伯努利、普瓦松［Poisson］、波莱尔和其他经典理论家的理论——实际上我在《逻辑》中解决它时也是这么做的。因为在这个方面我一直反对冯·米泽斯。我一直在强调这个问题，甚至可能是声音最响亮的一个，但冯·米泽斯却相信这根本不是问题，还认为我们必须接受如下观点，即随机序列的存在是一个终极的经验事实。在他看来，概率理论所做的不过是记录这个事实，以某种理想化的形式来描述它。这种思想导致他得出了那两个他认为是不可还原的公理。

当他发现关于这个问题的经典解答都是循环的时候，他更加确信自己的观点正确。[25]这部分是因为他觉得我们不可能打破这个循环，部分是因为作为一个实证论者，他不相信“解释”，他放弃了推导的概念：自然中有些事实是不可还原的，只能被描述，无法被解释。

而我试图重建这个理论，因为我曾认为，虽然冯·米泽斯对经典理论的批判站得住脚，但另一方面，他作出的假定超出了数学理论需要的范围，因此他也就不可能对“机遇理论的基本问题”作出任何解答。所以我试图将他的假定缩减到最低限度，而方法就是表明我们可以在本质上从n-不敏感性这个观念——它等价于经典的独立性观念——出发推导出似机遇序列理论。[26]但我现在相信，冯·米泽斯对经典理论的反驳不成立，因为我看到了坎特利、科尔莫戈罗夫、瓦尔德、丘奇和J.L.杜布的工作，看到了他们所给出的理论形式，坦诚地说这部分还要归功于冯·米泽斯提出的一些概念。而且我也进一步相信，在杜布排除赌博系统定理的帮助下，我们已经非常接近于这个问题的最终答案了（如果我们接受趋向性假定的话）。

24　新经典理论和频率理论的对比

新经典理论和先前的经典理论一样，都将概率视为可能性（或特性、类或集）的测度。但它和经典理论的差别还是很大的，如下所述。

（a）它不以概率定义作为起点。相反，它把“概率”看作任何满足特定计算规则的东西。

（b）它不认为等分布或等概率比非等分布更基本。

（c）在许多非常重要的情形中，它都断言，特定可能序列的集具有0或1测度，并用这一定理取代了特定经典极限定理（其断言内容为：某些概率倾向于极限0或1）。

（d）它也允许其他诠释，但它强烈地支持——特别是通过其独立性理论——下述诠释：概率属于单一的出现或事件，而检验概率的手段是这些事件重复序列中的频率；也就是说，它支持概率的趋向性诠释。

下面我将依次简要阐述这几个要点。

（a）我们应当记得（对照《逻辑》第48节），经典理论[27]将概率定义为有利的可能情形与同等可能情形的比例。“同等可能的”在这里也意味着“同等概然的”，因此这个定义也就是要用等概率来定义非等概率；换言之，它等于这样一种看法：概率计算应当将等概率视为其基本概念，应当在这些基础上构造出一般计算规则。我将在（b）中更详细地讨论这个看法。

与此相反，新经典理论不打算采取拉普拉斯或冯·米泽斯的“概率”定义。它明确区分了两种任务，其一是构造概率数学计算的形式任务，其二是诠释这种计算在机遇对策中的一般应用。

拉普拉斯和冯·米泽斯在定义概率时都想到了应用层面。拉普拉斯想到的是骰子的六种概率，而冯·米泽斯考虑的是一个奇怪的事实：在投掷的长序列中，骰子出现的点数是无概率性的，但都是等频率的。因为在新经典理论中，“概率”意味着满足形式数学系统规则的任何东西。所以我们应当首先给出一个系统（同时着眼于数学的普遍性和可能的应用性）。至于对它进行不同诠释的问题则是后起的。

（b）新经典理论不以等概率的优选状态为假设，尤其是它不打算将所有概率构造为终极的等概然的“单位”或“位”的总和，换言之，它不打算将所有概率构造为计数可能性［counting possibility］的实际结果。

与此相反的观点还很流行[28]，例如常有人说只有唯一一种方法能估计概率的实际数值。考虑到这一点，我认为有必要补充几点批判意见。但首先我想重申的是我以前认可的一个观点（对照《逻辑》第57节）：等概率的假说性估计适用于对称的情形，它在物理学中非常重要。（[29]当然，我们无法从无差别原则中推导出这些估计，它们也不是可推导的；但正如所有假说一样，我们完全可以依据自己的直觉来猜想其内容（包括下述有趣的事实：等分布最大化了预测的不确定性）。

我的第一个意见是（正如冯·米泽斯常常强调的），哪怕是灌铅骰子这种简单情形——这显然是与物理学相关的问题——也超出了等概率问题的范围。

第二，我们应当知道，许多坚持经典概率理论的人（包括拉普拉斯自己），虽然一开始是从德莫弗的定义出发，但后来（有时就在写下这个定义之后）都发展出了某种完全与等概率假定独立的、更为普遍的理论，例如直接给出了二项式公式的一般形式。

第三，雅妮娜·霍西亚松［Janina Hosiasson］的批评[30]值得我们重视。其观点考虑了下述两种非常类似的机遇对策之间的差别。

第一种机遇对策可以描述如下：

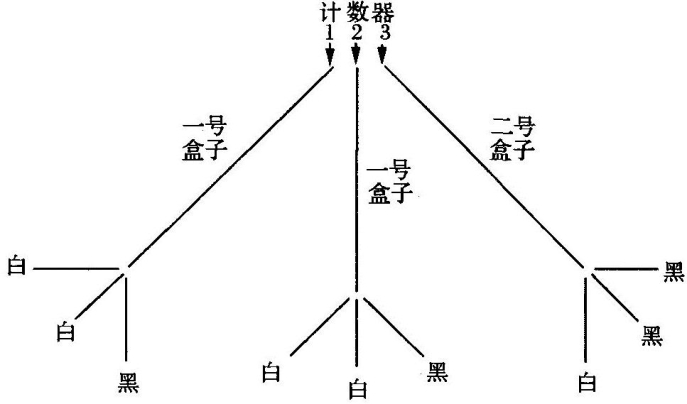
我有一只袋子和两个盒子，称为一号盒子、二号盒子。在袋子里有三个计数器，其中两个标着“一号”，另一个标着“二号”。在一号盒子和二号盒子中各有三个球；在一号盒子中，有两个球是白色的，另一个是黑色的；在二号盒子中，有一个球是白色的，另两个是黑色的。

我们从袋子中随机抽取一个计数器。如果它标着“一号”，我们就接着随机从一号盒子中抽取一个球；如果它标着“二号”，我们就接着随机从二号盒子中抽取一个球。当我们已经从不论一号盒子或二号盒子中抽取了一个球后，游戏便结束。现在请问抽中白球的概率。

答案当然是：

第二种机遇对策可以描述如下：

第二个游戏和第一个游戏完全相同，除了在二号盒子中只有两个球，一白一黑。

在此情形中，抽中白球的概率也很容易算出：

比较这两种对策，我们可以将第一种表示为以下图表：

而第二种对策的图表如下：

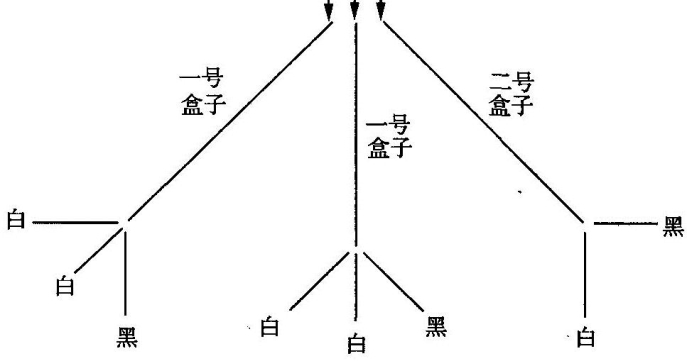
我们对第二种对策结果的计算可以表示为下面的第三个图表：

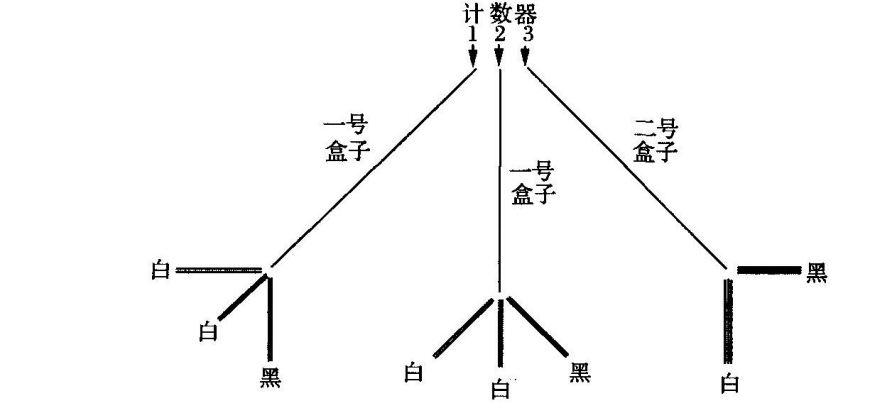
或者也可以表述为如下断言：这个图表“等价”于第二个图表。

现在我们可以将雅妮娜·霍西亚松的观点表述如下：

在第一种对策中我们本质上有九个相等的可能性。（正如图表明确表明的，我们也可以不用任何袋子，并且用两个不同的盒子都标上“一号”，来代替原来的那只一号盒子，这样的话三个盒子里一共有九个球，其中五个是白色的。）我们可以这样表述我们的结果：首先我们数出完成游戏的所有相等方式或相等可能性（共有9种），然后再数出抽中一个白球的可能性的数量（结果为5）。那么比例就是答案。

但这个方法并不适用于第二种对策。其结果是，但如果说我们有18种可能性，而其中11种是有利的，那么这种说法显然不是真的：任何可能性的计数都无法产生此结果。虽然第二种对策也很简单（在计算过程中没有丝毫困难之处），虽然它在每一步骤中都是等概率或等可能性的，但计数（相等的）可能性的理论却无法得出其结果。它包含某种“18种等概率”的假想构造，我们无疑可以计算［calculate］出这些等概率，但它们在第二种对策中绝对不是真实存在的。因为即便第三个图表描述的对策“等价”于第二个对策——任何对概率计算略有所知的人都能一眼看出这一点——但实际上它描述的是一个新的对策，完全不同于第二种。而这第二种对策（有8种不相等的可能性）和第三种对策（有18种相等的可能性）之间的“等价”，我们既无法先于计算构造而“看出”它，也无法将之“假定”为计算的基础。

总结一下上面的论证。在第二种对策中，有8种不同取球方式，其中5种能取出白球。但这些可能性是不相等的（无论原因为何），并且是计算的结果告诉了我们答案为，而不是据称相等的可能性计数告诉了我们这一点。换言之，虽然问题是依据相等的可能性的存在来加以表述的，但其结果——虽然非常简单——却不能用这种方式来表述。这表明基于相等的可能性计数的任何定义都是不适当的。

（c）在新经典理论中，表明了某些集具有0测度（或1测度）的定理代替了具有一定重要性的极限定理，这一代替有着哲学上的重要意义。一方面它解决了概率理论中某些据称的悖论，另一方面它帮助我们搭建了一座连接概率假说与依据相对频率的检验的“桥梁”。

最近这些据称的悖论成了人们讨论的热点。[31]它们与有时被称为“库尔诺［Cournot］原理”（或“库尔诺引理”）的东西有关。这个原理可以表述为“概率很小的事件实际上不可能”。[32]这个原理（以及任何类似的原理）问题就在于，事实上那些概率很小的事件确实发生了，哪怕非常罕见。用保罗·伯尔内［Paul Bernays］的话来说：“我们无疑能构造出库尔诺引理的反例（例如我中了彩票头奖）。”[33]（此外，所有充分复杂的实际出现其概率都非常之低。）

在概率理论中这个问题呈现为两种非常不同的形式。第一，它呈现为桥梁问题——从概率到频率的转换；第二，它呈现于频率理论之中（呈现为概率陈述的可检验性问题，我在《逻辑》中对此有详细讨论）。

上述第一个形式问题完全可以通过由新经典理论推导出来的新频率理论解决。也就是说，通过推导出来的强大数律以及杜布作为“几乎确定的”赌博系统的无用性定理来解决。

因为这些结论的推导过程的概率精确地等于1；因此例外的概率精确地等于0，而非接近于0。准库尔诺原理涉及的是等于0的概率，不可能存在关于它的经验反例：不可能有中奖概率等于0的头奖彩票。

诚然，不可能存在反例这个情况，和下述事实有很大关系：新推导出来的理论和零概率涉及的是无穷序列，而我们不可能产生一个经验事实的无穷序列，我们也不可能用无穷数量的彩票去赌一次头奖。然而，无穷序列的收敛定律和随机性定律构成了频率理论的基础；在其推导中，所有的差别都来自我们要避免仅仅接近于1或接近于0的概率。

如果我们还记得冯·米泽斯对这个“桥梁”的批判，我们就能清楚地认识到这一点。[34]他指出，为了使用伯努利定理或普瓦松定理来证明从经典概率陈述到频率陈述的还原过程，我们必须先验假定这样的辅助原则：“一旦我们通过计算得到只比1小一点的概率，那么这个事件在实验的几乎所有重复中都会发生。”但冯·米泽斯也指出，如果我们将0.999这个概率诠释为“几乎总是”，那么就必须“立刻承认0.50这个概率意味着在100次情形中平均有50次会发生这个事件”。换言之，这就等同于立刻采用了频率定义。

但新推导出来的理论在此有所不同。

首先，它解决了下述难题：将0.999这个概率诠释为意味着“几乎总是”，这为什么不能令人满意？无论多么接近1，总需要一个等于0.999的频率极限之类的东西，也总需要“0.999这个概率对赌博系统不敏感”这个陈述。换言之，如果我们打算在频率的意义上诠释0.999，我们就需要整个频率理论。但如果我们得到了一个精确地等于1（或等于0，这是零测度的情形）的概率，情况就不同了。当然，即使在这一情况下，“概率”也必定意味着某些与频率有关的东西，如果我们希望得到需要的结果的话。但我们不再需要确保任何精确的关联——例如极限公理和随机性公理；因为显然它们是无效的，除非概率（测度）为零，但这样的话我们就可以忽略之。因此我们需要确保的仅仅是，在随机事件的情形中，零概率（或零测度）意味着作为非概然性而可以忽略不计的概率。

其次，如果我们希望以这种方式诠释“概率”，那么我们必定要承认0.50这个概率意味着100次情形中发生50次的概率为1。现在我们可以证明这个结论成立，但我们并不需要在证明中假定某种频率定义。因此频率定义是不充分的，这并不构成什么问题。实际上它根本就是不必要的：即便不假定概率意味着某种频率极限，我们也可以推导出与频率极限相关的种种结论；因此我们可以做到赋予“概率”某种更广泛的、更模糊的意义，而在这过程中却不会威胁到那座桥梁的安全——这桥梁的一边是概率陈述，而另一边则连着服从于统计检验的频率陈述。

无论如何，只有客观地诠释经典理论——例如在趋向性诠释的意义上——我们才能建造这座连接经典理论和统计学的“桥梁”。至于主观诠释，我以前作出的那些批判是适用的。（见《逻辑》第48节注释6，和第62节注释3。）

（d）我们已经知道，新经典理论并不定义“概率”，因此也不打算像经典理论和冯·米泽斯理论那样，从“概率”定义中推导出计算方法。相反，它首先构造的就是计算方法（或者是依据某种公理学方式，或者是将之作为测度论的一部分）。随后引入的就是种种关于此计算的诠释，例如主观的或客观的。但主观诠释在独立性理论中是失败的，这促使我们必须采用趋向性诠释。

然而，严格意义上的冯·米泽斯式的频率诠释（虽然我曾说过它是一致的，也是高度令人满意的）却无法支持新经典理论的可能诠释：新经典理论确实更为普适，它蕴涵了频率理论，并将之视为某种“首次逼近”。

因为除了频率诠释和趋向性诠释之外似乎不再有什么客观诠释，也因为频率诠释本身不可能成为“桥梁”，所以我认为唯一能够诠释（新）经典理论的就是趋向性诠释了。

这关联中的要点在于，这个新的理论确实能够赋予单称事件以概率。[35]虽然它考虑了事件的序列以及在这些序列中的频率，但是，在序列的某些被观察的节段中，一个事件的概率与其频率可能极为不同。（它仅仅符合几乎所有序列的频率极限。）

上文我试图说明冯·米泽斯类型的理论不可能诠释新经典（集合论的）概率理论的形式表述。[36]但乍看之下，似乎我们有可能调和这两种研究方法——即新经典方法和频率方法。因为有人会提出，下述关于新经典理论的频率诠释有可能实现冯·米泽斯之类频率理论家的主要目的：

（*）我们将新经典理论中所用的表述“事件x的概率（或测度）”诠释为意味着“在无穷序列集（随机或似随机）的几乎一切序列中，x类事件的频率极限”。

显然，只要给定某一概率分布（或场或标定空间），诠释（*）总是可用的。它来自于强大数律和杜布定理。但下面我将表明，（*）极度令人不满意：它实际上是本末倒置了，另外它还使问题情境变得更为模糊。

这个诠释（*）显然不等同于频率理论，但在内涵上二者是接近的：频率理论家应当会乐于将它视为某种推广，他们会提出下述论证来支持（*）。

在第一个实例中，“概率”意味着有限事件类中的相对频率，而在第二个实例中，它意味着无穷事件序列中相对频率的极限。在涉及无穷序列时，我们可以谈论“分布”，也即总和为1的种种基本概率，这个总和就是事件基本特性或类型的频率极限。而我们总有理由将分布视为相对于序列的类的——这些序列在名义上具有相同的给定分布——而非将其视为相对于一个序列的（这是冯·米泽斯之类频率理论家的看法）。这在本质上并没有改变下述频率学说：概率和分布仅在相对于一给定参考序列时才有意义。在这些新的形式中，它们在相对于所有那些属于某个参考序列集的参考序列时都有意义。这个集可以被称为“参考集”。最后我们甚至可以扩展这个参考序列的“参考集”，使之包括其频率与概率不相同的“例外序列”，假定这个参考集的测度为1，而且例外序列集的测度为0。这样一来，从频率理论的观点而言，我们就会发现（*）是关于概率计算的一个完美的自然诠释。

但我认为这个论证完全混淆了问题的情境。

因为我们只能在相对于一个基本分布，或称场、或称“空间”的意义上，谈论新经典理论意义上的概率或测度。如果没有建立这个分布，我们根本无法谈论任何序列集的测度。但这个分布是一个概率分布。因此，我们以某些特定的概率作为出发点，建立我们的测度系统，这是其他概率的系统。（正如冯·米泽斯自己一直强调的，概率是给定的，我们从它们中推导出其他东西。）所以“参考集”具有测度1，而“例外集”具有测度0，而这仅仅相对于我们的初始分布，也就是说，相对于在出发点时给定的概率；如果用一个测度1的序列集来说明概率，那么就是本末倒置了，因为换个初始分布（即在不同的空间形成的排列）集的测度也许会变成0。换言之，如果给定了所有可能的交错序列的连续集，那么对于一个初始分布来说，具有相应频率的交错序列的子集A其测度为1，而根据另一个分布，子集A的测度为0。[37]因此我们不可能用（*）来解释（或定义）“几乎所有序列的频率”这个意义上的“概率”。因为“几乎所有”翻译过来就是“测度0”，原本与分布相关，也就是说，与假定的初始概率相关。因此（*）确实是提供了一个可能的诠释，但它不能令人满意。

25　新经典理论的结构

上述观点极为重要。它表明，令人满意的诠释不会根据频率来解释p（x）；换言之，它表明单一事件或出现的概率虽然在某种程度上与频率有关，但其结论是频率诠释无法穷尽的。

在新经典理论中事件频率和概率的关联方式证明了这一点。一个事件——例如事件序列中的第m个事件——具有特性P的概率，这个含义如下所述：

第一步，我们考虑由排他性的、穷举性的特性P、P'、P''…组成的一个基本集，它们是事件所呈现的特性，我们（自由地或猜想性地）赋予每一个特性一个小于1的正数，并使这些数的总和等于1。

这些自由指派的（或猜想性估计的）数字将成为属于这个基本集特性的概率。因为我们可以自由选取（或猜想性地估计）它们的值以满足总和等于1这个条件，所以在这里我们得到了旧的经典方法的推广（根据旧理论，这些数字都是相等的）。

接下来的两步将引入（概率的或随机的［stochastic］）独立性理论或联合出现概率理论。从本质上来说，它们的理论基础是所有可能序列以及附属于这些序列的测度。

因为我们不知道实际的序列是什么，所以我们打算构造所有可能的序列，方法是写下：

（1）实际序列的第一个事件会呈现的所有可能特性；

（2）实际序列的前两个事件会呈现的所有可能的特性组合；

（3）实际序列的前三个事件会呈现的所有可能的特性组合，等等。

我们可以将特性的这些具有不同可能性的组合称为可能序列。

如果基本特性的数量大于一，那么显然有：

（a）可能序列数量的增长速度必定快于其长度——实际上致少有2n那么快。

（b）在第m个位置上，每一个特性必定发生在至少2m-1个不同的可能序列中。

但这意味着如果我们考虑一个无穷事件序列，因此有一个无穷长度的可能序列组成的集，那么我们有：

（a）所有可能序列组成的集U是一个（连续统的基数性的）无穷集。

（b）在第m个位置上具有特性P的所有可能无穷序列组成的集S（m，P）也是一个（具有同样基数的）无穷集。

但在旧经典理论的意义上，我们应当将集S（m，P）被集U的数量所划分的数量，诠释为第m个事件具有特性P的概率。

考虑到事实上这些数量是无穷的，我们给集U赋予测度1，至于集S（m，P）的测度，我们令它等于我们在第一步中给特性P赋予的值。因此这个值也就等于经典的概率比值，现在我们认为它就是第m个事件具有特性P的概率。

以上是第二步。对于所有m和n，它将第m个事件和第n个事件的概率视为相等，因此就确保了对位置选择的不敏感性。

第三步将确定其第l、m、n…个事件具有特性P、P'、P''…的序列的测度，（1）对于特性P的情况，它等于其第l个事件具有特性P的序列集的测度的乘积；（2）对于P'的情况，等于其第m个事件具有特性P'的序列集的测度的乘积；（3）对于P''的情况，等于其第n个事件具有特性P''的序列集的测度的乘积；等等。这就是说，它确立了独立性的乘积规则。

这样一来，它将在数学上产生许多重要的定理，其中有：

（ⅰ）其频率不收敛于概率的序列所组成的集具有测度0。（因此，具有非收敛的频率序列的集具有测度0。）

（ⅱ）根据任何给定的赌博系统，对选择敏感的序列组成的集具有测度0。（这是杜布定理的推论。）

因为我们将零测度诠释为零概率而非不可能性，所以我们没有排除存在与冯·米泽斯理论相矛盾的序列的可能性；但我们也已表明，踫上此类序列的概率为零。

在这个理论中，概率是推广了的可能性测度；但借助伯努利方法的一些基本理论，我们发现具有偏离概率分布频率的序列非常罕见，以至于我们可以忽略它们的出现。

因此，作为可能性测度的这个概率诠释，其基础正在于新经典理论的结构中。

在新经典理论中，概率和独立性这两个概念都在逻辑上先于频率计算；它们也不可能被还原为频率。但关于概率或独立性的新经典陈述允许我们以1的概率断言，关于频率的关键陈述为一切物理学应用所必须。

26　单称概率陈述

频率理论和新经典理论之间最重要的差别体现在关于单称概率陈述的诠释上。我在《逻辑》第73节中非常详细地讨论了关于单称概率陈述的频率诠释，它等同于断言：陈述“下一次硬币抛掷结果为正面朝上的概率是一半”和假说“此枚硬币的抛掷（有限或无穷）序列中正面朝上的相对频率是一半”，这两者的意义一样；也就是说，这个句子只是看上去是单称的，其实也应诠释为序列中的某一项。

与此相反，新经典理论将单称概率陈述诠释为这样的陈述，它赋予单一事件——更确切地说是某一单一事件和此事件可能发生或不发生的环境集——以概率。

如果某种概率理论是直接赋予单一事件或单称陈述以概率，而无需通过序列集的方式，那么我就将此理论称为“单一事件理论”。[38]

我们常能听到这样的观点：如果想得到“单一事件理论”，我们就必须能使此理论将概率诠释为理性信仰的程度，也即某种主观理论或逻辑理论；尤其是，如果我们希望一个基于概率或等概率的经典（拉普拉斯的）定义不至于太过狭窄的话，这就是必须的。[39]看来很多相信合理信仰程度的人都这么做，因为他们希望采用的是一个不基于等概率的“单一事件理论”。他们相信（但理由不是很能说服人），只有采用主观理论或逻辑理论，他们的上述希望才能得到实现。

但是，我认为没有任何理由表明经典理论和新经典理论——它们认为概率是一种估量（或测度）——就不可避免的要与等概率联系到一起。相反，等概率显然只是一种确立估量或测度的方法而已，在理论数学发展的实际过程中，它起到的作用一直都很小。

我将在下一节中进一步批判概率的主观理论和逻辑理论。在此我只打算说明，没有任何理由要相信，如果抛弃了等概率方法，我们就只能要么局限于频率理论这一方，要么局限于主观理论和逻辑理论那一方。为了说明我的观点，我将首先讨论一个等概率情形，一粒完好的骰子，然后再用灌铅骰子来改变此情形。

在完美骰子的情形中，对于下一次投掷的六种可能结果，我们将赋予其相等的概率。这里涉及到的是下一次投掷——一个单一事件。问题恰恰在于，我们如何谈论这个单一事件（除了断言说它潜在地属于具有某一频率分布的序列）。

我认为我们可以这样来分析这个单一事件——下一次投掷——的断言内容。

（1）我们事先决定，我们仅仅考虑投掷后六个面中朝上的那个面。（因此我们将忽略哪个面朝西等等这样的问题。）换言之，我们进一步限定了我们要考察的“可能结果”。

（2）此事件发生（或此实验进行）的客观条件使我们无法预测其结果。（这一点并不算关键，因为我们可以将完全可预测性诠释为概率等于1的断言。）

（3）我们猜想，对于每个可能的结果及其逻辑组合（尤指它们的析取或逻辑和），都可以给出一个满足概率计算公理、特别是加法定理的数字，因此这数字能被诠释为某一加性测度［additive measure］。于是数字1对应的是我们考虑的所有可能结果的析取（求并集），而数字0对应的是两个互斥结果的合取（结合，求交集）。

（4）这些数字是为了测度种种可能性，而这些可能性向着事件或实验的条件开放：如果这些条件在客观上对于这些结果是对称的，那么我们可以通过假定这些数字是相等的，从而得到它们。

（5）我想着重强调，在此分析中我们在赋予概率时假定了下述前提：条件具有客观对称性。而对于特别的骰子而言这个假定是错误的（实际上所有骰子都会有轻微的不对称性），这样一来，我们给出的相等数字——即等概率——就是错误的。但我们假定：

（6）所有与对称性或同质性的轻微偏离都对应于与等概率的轻微偏离。

上述分析针对的是（几乎）同质骰子的情形。它将某个数字（可能性或概率的测度）赋予事件的客观环境，而不是赋予我们的知识能确保的信仰（客观合理）程度。

为了表明此中差别，假定有一粒骰子，而我们的问题是去决定投掷结果的概率分布。根据我的分析，正确答案是这样的：“我不知道。我能说的仅仅是，如果这粒骰子是近似同质的，那么概率就应当大致相等。”

现在让我们考虑一粒灌了铅的骰子，机器检测发现，灌铅部分偏离中心，偏向标着“1”那一面的反面。

（1）我们可以说，如果灌铅部分位于中心，那么等概率就近似地保持；如果稍有偏离，那么等概率也将相应地稍有偏离（可能可以忽略不计）；而我们关于物理机制的知识告诉我们，上述偏离意味着出现“1”这一面结果朝上的概率（可能性）将会增加。

（2）如果有人问我们“你如何确定这个微小的偏差？”我认为正确的回答是这样：“我不知道。”我不认为我们能从已知的离心率计算出它与等概率的偏差（这也是韦尔的观点[40]）；因为概率分布不仅是灌铅骰子本身的特征或特性，也是所有相关条件的特征或特性。例如，它有可能部分取决于骰子坠落的表面——这个表面是钢的、橡胶的、天鹅绒的平垫子、覆盖着沙或泥土，等等。（对照上文第21节。）

（3）但是，虽然我们无法在计算灌铅骰子的概率分布时应用对称性理论，但我们总还知道一些别的信息。例如，我们知道灌铅的位置无论偏离中心的程度“小”或“大”，它都能增加“1”的概率；这又蕴涵着如下事实：存在某一附属于此单一事件特定条件的概率分布，虽然我们并不知道它。

（4）有人断言说，这样一来，岂不是那些我们不知道的和我们常常无法计算出来的数值刻划了物理事件的性质？但这个诘问并不构成对我观点的反驳。在数学和物理学中，我们经常都会去讨论一些其数值还无法（或无法精确地）指定的函数，并得到具有重要意义的结果。

（5）概率值的精确判定都带有不确定性，在我看来这恰恰标志着概率的客观性。让我们再来考虑灌了铅的骰子。我们有可能很精确地知道它的离心率和其他相关条件。但我们的这些知识可能还不足以在我们想要的精确度层次上判定概率，哪怕它能使我们作出“这个分布是不相等的”此类断言。确实存在着一个客观概率，但我们不知道它，或者说迄今为止仍然不知道它。虽然我们可能没有时间作出一个足够长的序列来满足精确判定的要求，但我们有可能知道如何测度它。

根据主观理论，我们的知识状态确切地判定了任何时刻的概率。虽然在实际中依据我们的知识状态来计算概率会有很大困难，但对于所有的知识状态，这是一个确切的数值，因为它是我们知识状态或知识缺乏的测度。根据这个观点，用重复实验的方式——即用不断探索进一步知识的方式——来谈论这个概率的测度毫无意义，因为进一步的知识一般而言都会改变概率。（参见前一章。）

而在我看来，实验的重复不会改变概率；因此我们应当进行这些实验，以改进我们对客观概率估计的精确性。

27　对主观理论和逻辑理论的进一步批判

在开始分析单一事件的客观概率之前，我打算从稍微不同于前面章节的观点出发，对主观理论和逻辑理论再做一些批判。

我很乐于承认，我们当然可以毫无问题地将概率计算诠释为针对理性期望程度（或类似的东西）的计算，而在这样做的时候我们既可以采用主观或心理学的方式（例如拉姆齐、古德或开米尼），也可以采用逻辑的方式（例如杰弗里斯、凯恩斯或卡尔纳普）。[41]

在这里我打算批判下述观点——它认为上述诠释正确地阐述了概率在物理科学中的用处。

在我看来，物理中的陈述是客观的，在任何程度上它们都不涉及我们的信息状态：它们既不“表述”我们的信息，也不“表述”我们的无知。它们是一些关于世界的断言——当然这是猜想性断言。

这一点对物理科学中的概率陈述也适用。它们不是我们缺乏知识的产物。知识的缺乏不会奇迹般地产生关于频率的知识——即便在大数律的帮助下也不会。

频率假说——例如关于光谱线密度的频率假说——和其他所有物理假说一样客观，那些否定单一事件概率客观性的人也可能承认这一点。但我认为，这其中的差别相对而言是很轻微的。客观的单一事件概率产生了（依据波莱尔—坎特利定律和杜布定律）客观的频率陈述。另一方面，表述了合理信仰状态的概率只能产生涉及合理期望频率的陈述；如果诠释是主观的，那么“合理期望”就是主观的，而如果原来的诠释是逻辑的或重言的，那么“合理期望”就是逻辑的。

在单一事件客观概率的情形中，我们首先在单一事件会发生的前提下估计其客观条件；然后我们用数学推导的方法，在特定频率会发生的前提下估计其条件。在主观概率和逻辑概率的情形中，我们首先估计的是“数据”——即信息“给定”的陈述——与事件陈述之间的逻辑关系；然后我们用数学推导的方法[42]，估计这些同样的数据和特定频率陈述之间的逻辑关系。这样一来，我们所获得的东西仍然与我们的信息相联系；我们并未能像客观概率假说的情形一样，推导出频率假说，从而检验它或者视需要否定它；我们获得的是（假定计算是正确的）真的陈述（实际上是重言陈述），它涉及的是我们给定的知识确保特定频率的期望的程度：我们得到的不是物理猜想，而是关于我们自己知识状态及其内容的自明之理［truism］。（见前一章。）

再来考虑骰子的情形。主观理论和逻辑理论并没有真正地去处理物理学家们所关注的下述问题：这粒骰子的行为如何？这两个理论并不能真正产生下述问题（当然这问题是不可回答的）：下一次投掷会是哪一面朝上？它们询问的是另一个不同的问题：“我们的数据在什么程度上允许我们作出关于这粒骰子行为的某种陈述？”在涉及到下一次单一事件时它们也只能询问：“我们的知识（或无知）在什么程度上允许我们预测下一次投掷将得到一点？”[43]

我关注的是骰子的行为，而我相信大多数物理学家也是如此。我想了解它的秘密，我准备提出某种猜想——例如，在特定条件下作出的长投掷序列中它每一面朝上的频率都是相等的；又或者，这些条件确立了所有面都是对称的。

与此相反，主观的和逻辑的理论家们关注的是他们已经对这粒骰子了解了多少，而不是关于它行为的猜想。例如他们会发现，至于下一次投掷结果究竟是六个面中的哪一面朝上，他们都是一样的无知，因此这六个概率是相等的。

假设我们现在有了一个投掷序列3、1、5、1、2、2、3、5。主观的和逻辑的理论家们必定断言，这些新的数据肯定会影响下一次投掷的概率。下一次的概率将或多或少地改变：发生4和6的概率会（或多或少地）减少，而发生1和2的概率会增加，因为4和6根本就没有发生过，而1和2各发生了两次。

现在假定这粒骰子是同质的，那么这个序列就变成一个正规序列。那么主观诠释和逻辑诠释意义上的概率将一直都发生轻微变化，并最终逐渐接近于等分布。长投掷序列和新“数据”的总体影响是零。因此这个数据将变成“基本上不相关的”。[44]

另一方面，从客观理论——无论是单一事件还是频率类型——来看情境都大不相同。从这个角度来看，投掷序列构造了一个对假说的统计检验。如果我们从一开始就怀疑骰子有问题，那么检验将会反驳我们的怀疑。因此我们就可以宣称，它验证了我们关于等概率的猜想。

根据这个观点，主观诠释和逻辑诠释混淆了有关客观物理系统的物理陈述，以及“我们的经验支持”这些陈述程度的认识论估计。

要对这个错误负责的，不仅是“所有单一事件理论都必定要么是主观的要么是逻辑的”这个错误信念。新的“信息”有可能以多种方式改变概率，这个无可置疑的事实似乎也让许多理论家相信，概率不可能描述实验条件的客观特性：如果我们“被告知”投掷结果是一个偶数，那么投掷两点的概率就是⅙或⅓，用符号来表达就是：

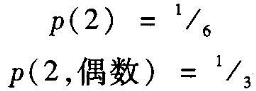
无疑事情确实如此。但这个公式在将“偶数”这个词诠释为“信息”时，它已经采用了一种主观或逻辑的诠释。（这不意味着在客观理论的上下文中我们也无法使用“信息”这个术语，我们只需提防不要被术语所误导，混淆了两种诠释。）

从客观观点来看，“p（2）”和“p（2，偶数）”涉及的是两个不同的实验安排：前者涉及的是考虑了所有投掷的实验安排，而后者涉及的是我们决定忽略那些结果为奇数的投掷的实验安排。因此我们也可以这样说：符号“偶数”所表述的“信息”告诉我们，我们在询问的是一个不同的问题——我们不再去问“投掷两点的概率是什么”，而是去问“在只考虑那些结果为偶数的投掷前提下，投掷两点的概率是什么”。[45]

28　单一事件的概率之趋向性诠释

在前面两节中我试图表明，哪怕单一事件理论不以等概率作为基础，我们也没有理由就此认为客观的单一事件理论不可能成功。

但我也承认，将概率视为可能性的测度，这个观念仍然略显单薄。尤其是，这个公式显然不能被视为定义：我们都知道，此处的“可能性”不过就是“概率”的同义词而已。无论如何，它就像“频率”一样，其意义并不比“概率”更清晰。

然而，我并不打算定义“概率”——也不打算定义“单一事件的概率”：我们需要的不是定义（因为我们有一个公理系统），而只需要诠释；我也将给出一个诠释，并使它在直觉上比“可能性的测度”这个说法更可接受。我的建议是将单一事件的客观概率诠释为某种客观趋向性的测度；所谓趋向性，也就是内在于特定物理情境中的某种倾向的力度，它将实现此事件——使此事件得以发生。

能打保票的是，我的那些实证论朋友们听到这个想法，恐怕会惊讶得下巴都要掉下来。在他们看来，这简直就是我屈从于形而上学的一个明证。也许我不该写什么“倾向或趋向性”，可能“意向”更合适一些。

我不相信什么词语的魔力，我也不介意用“意向”来代替“趋向性”或“倾向”。但我想强调的是，正如大多数说明性假说一样，关于客观概率的假说也超出了观察所提供的知识界限，在这个意义上它也是超越性的。（对照《逻辑》第25节末尾。）这一点对于客观频率假说也适用，另外，对于那些通过解释频率从而涉及单一事件客观概率的假说，它们具有更高的程度（因为它们的普遍性程度更高），而上述这一点对它们同样适用。

为了详细地阐述关于单一事件客观概率的这种诠释，我将首先指出，趋向性1意味着事件确定或至少几乎确定会发生，而趋向性0意味着事件确定或几乎确定不会发生：在这个界限内，两种客观诠释都相当一致。但符合0≠p≠1的趋向性p意味着，第一，在所考虑的环境中此预期事件有可能发生也有可能不发生；第二，如果还有p＞½，那么它意味着此特定环境更有可能使事件发生。

但在这一点上人们有如下问题：如果不是环境本身，而是我们对此特定环境的知识缺乏，产生了不同于1或0的概率，那么情况又如何呢？如果真是如此，那么我们就必须放弃客观理论了。而如果不是这样，那么我们似乎也只能将客观理论应用于非决定论的事件中；在这里非决定论的意思是，甚至是关于“环境”的最完备的知识都无法得出可预期的结果。但实际上，我们希望这个理论能应用于硬币抛掷这类宏观物理事件中，而在这个情形中没有人会相信它们是非决定论的。

这是一个很重要的反驳，它促使我们这些客观理论的拥护者们深人到问题的核心层面。

我们考虑一台硬币抛掷机：放一枚硬币在槽里，按下按钮，硬币就会水平地掉落到软地毯面上。在观察机器的一两次投掷行为之后，如果有人问我打算赌正面还是反面，那么我认为某种合理的回答是这样的：“我不知道这个机器是否能使其结果随机化（正常的轮盘赌机能做到这一点）。据我所知，根据这个机器的构造，如果我在按下按钮时使用某种特殊的方式（或类似的技巧），它就能产生出我所期望的结果。”而考虑另一种情形，硬币在我们面前的一个不平的表面上不断翻滚，并最终以较大的速度掉到一个大瓶子中；此情形和前述情形大不相同。在第一种情形中，我们会说我们很怀疑实验的客观条件能够确保机械初始条件的某种“随机性”，而在第二种情形中，我们确信条件是随机的。

在两个情形中都出现了知识的缺乏。在第一种情形中，我不知道客观条件具体如何，而那些知道的人则有可能得以轻易地作出精确的预测。因此对于那些知识比我丰富的人来说，第一种实验是可预测的，甚至可能是可控制的。

在第二种情形中，境况大不一样。能用于预测结果的初始条件是“随机化的”，这正是实验条件的一部分。我的意思是，我们安排这些初始条件的方式，就在于使得我们能作出如下猜想：在同样的特定条件（包括“随机性”）下进行的实验长序列中，机械的初始条件倾向于以随机的方式发生变化。

正是这个肯定的猜想“实验的特定条件确保了初始条件的随机性”构成了我们关于客观概率假说的基础：我们的猜想是，如果我们的实验是重复的，那么它们的特定情形就能产生随机的初始条件。

但如果有那么一个人，他能非常迅速地测度和计算实际滚动的硬币和不平表面的种种初始条件，而且能在硬币刚好掉落到瓶子前的一瞬间做出正确的预测，那么情况又将如何呢？我的回答是这样的：他的预测与我们对这些单一事件客观概率的估计并不冲突，正如他的预测与频率诠释不冲突：无论我们能否在事件发生之前的一瞬间知道其结果，频率都依然是稳定的和随机的。单一实验的趋向性也是如此——更精确地说，单一实验组织的趋向性也是如此。因为在我看来，“趋向性”指的就是产生这些频率的实验组织的意向（或此类东西），只要实验重复的次数足够多。趋向性是产生频率的意向，这也正是新经典理论所支持的诠释。但“趋向性”的意义不是“频率”，因为有一些重复发生的事件极少能产生随机序列的良好片断所蕴涵的那种东西（或曰某一“频率”）；但这些罕见的事件同样也有趋向性。

因此在这粒骰子的情形中，数值1/6于是被诠释成为此实验安排定了性，即便我们可以通过非常迅速的计算或预先识别，预测到这个投掷的长序列的每一次结果，这个性质也依然保持有效。这个数值附属于单一实验组织，其依据是我们所知道的东西，而不是我们知识的缺乏。而附加的知识不会影响这个为实验组织定性的概率或趋向性。

但仍有一个值得考虑的问题需要解决——我们为何会相信像硬币在不平表面上翻滚这样的过程将使初始条件随机化？对于这个问题，我将在《后记》第二卷第29和30节中再进行讨论。（朗代［Landé］的片。）

在这里我仅打算做两点说明。第一，在谈论趋向性时，我想表达的是一个类似于牛顿的力那样的直觉观念，但它和力的不同之处在于它产生频率而非加速度。频率随趋向性的改变而改变。趋向性像牛顿的力那样是“超越性的”或“形而上学的”（贝克莱抨击后者是“超自然的”）。在数学上它们是极为明确的——它们是简单计算的诠释。至于其可检验性，我们必须根据可从它们（以概率1）推导出来的频率陈述。但即便那些超越了频率陈述的部分在某种意义上也是可检验的——可用频率陈述或其他陈述加以检验。（通过分析量子理论就能认识到这一点。）

我想说的第二点是这样的。我相信趋向性诠释是关于经典统计力学的诠释。玻尔兹曼谈论过倾向。但我认为，在谈论等似然的情形与所有可能情形的比例时，我的这个术语能更好地表述经典理论家们心中真正所想的东西：他们所想的是，这个比例是在特定具体条件下，产生特定事件的趋向性的一个测度（一个非常重要而又方便的测度，虽然不是最普遍的）。

虽然《逻辑》中有大量章节与逻辑概率有关，但我承认在写它时我是一个支持频率理论的人。当时我强调指出，对概率计算存在着诠释的多元性；但当时我也仍然相信，频率诠释在物理学的具体实践中有着根本的重要地位。

从新经典理论推导出的频率定理有着极为关键的价值，就这一点而言，我依然可以坚持上述立场。但我现在觉得，更重要的是要强调我观点发展中的非连续性，而不是连续性，因为我已改变了许多想法。从历史而言，当我努力试图理解量子理论中的情境时（关于此点的详细讨论参见《后记》第二卷和第三卷），就首次发生了这个转变：正是在那时我首次认识到我需要趋向性诠释。我从那里出发，回到了概率理论中，并且非常满意地发现新经典理论确实提供了支持趋向性诠释的数学基础，它建造了一座“桥梁”联系起经典理论和频率理论，起初我受到冯·米泽斯的影响，还以为这座桥不可能建造出来。

实际上，我能证明我绝不是以先验的形式引入趋向性诠释的。它解决了“机遇理论的基本问题”（对照《逻辑》第49和64节）。也就是说，它解释了为何几乎所有硬币抛掷序列的行为都会呈现出如此令人吃惊的方式：为何长序列的行为就仿佛它们的相对序列倾向于有一个极限；为何它们会呈现出这种奇怪的规律性和作为其特性的无规律性二者之间的混合；以及为何它们的节段看来完全服从于伯努利定律。

总结　1982年

（1）本书最后一章的主题是说明，（我在《逻辑》中所谓的）机遇理论的基本问题现在已经得到解决，而且解决的方法优于《逻辑》中给出的方法。这个令人头疼的问题可以表述如下：

所有记录下的硬币抛掷或骰子投掷序列都呈现出两种性质，一方面是典型的随机性质，另一方面则是似乎倾向于某一极限的稳定的相对频率。对此我们如何解释呢？

我认为，如果我们采用概率计算的趋向性诠释的话，上述问题就能得到完备的解决。而这个计算本身只是转变成了命题逻辑（参见《逻辑》新的附录*ⅳ和*ⅴ）的一个测度性质的推广——在此命题逻辑中增加了一个众所周知的、非常令人满意的关于事件独立性的定义。

由趋向性诠释所诠释的这个计算允许我们演绎出如下结论：

（A）在恒定条件下发生的、由独立事件所组成的几乎所有无穷序列其相对频率都倾向于极限，而这些极限等同于单一重复事件的概率（趋向性）。

（B）几乎所有此类序列都具有随机性质，并可以通过多种方式加以描述，例如通过所有赌博系统在长序列情形下都会失败。

独立事件序列的这两个特征（A）和（B）是数学家冯·米泽斯[46]作为公设于二十世纪二十年代提出来的，他称它们为公理，并据此建立了一个概率的数学理论。但我已表明，如果我们将概率诠释为单一事件在长序列中实现自身的趋向性，那么我们现在就可以从一个简单的、几乎是逻辑的系统中演绎出它们。而从其他方面而言，这一点已是几乎必然的要求了。

这个重要的纯数学工作的开创者是雅各布·伯努利（《猜度术》［Ars Conjectandi］，1713年），他为之努力了二十年。这是一个伟大的成就。许多数学家随后继续着这项任务。我认为这是纯数学领域中的辉煌成功，也具有无上的哲学价值。这些观念帮助我们解决了世界上最伟大的迷，而理查德·冯·米泽斯仍然认为此迷是不可解的。

（2）我在本章中也表明，这个理论发展与概率计算的主观诠释不相容。

（3）从拉普拉斯以来许多最伟大的物理学家都普遍认为，我们必须求助于概率恰恰是因为我们知识的缺乏；爱因斯坦在写给我的两封信中（其中一封重印于《逻辑》）也为这个观点做辩护。主要说来，正是因为这个原因，我在本书中竭尽全力地搜集了许多论据（我甚至担心有许多地方都重复了）以期表明，客观诠释能解决这个问题，而主观理论无法做到这一点。

（4）爱因斯坦对“玩骰子的上帝”[47]的著名拒绝无疑是基于他的下述观点：概率理论是一种权宜之计，它的根源在于我们知识的缺乏和人类的可误性；换言之，他相信概率理论的主观主义诠释，这个观点显然与决定论相关联。在我和他会面时，我曾试图说服他，这个观点应当被否弃掉；而从1954年3月31日泡利［Pauli］给玻恩的信来看，爱因斯坦（显然在我们会面开始时他仍然坚持这一点）确实否弃了它。[48]

（5）我还想补充一点：机遇理论的基本问题的解决至少让我们看到了解决因果问题的一种可能途径。在某些情形中，（表面上的）因果律可以作为统计性整体效果（例如基于普朗克量子的微小性的波义耳定律或因果定律）而被推导出来，这一点显然打开了通向问题答案的大门。另外，我认为没有任何理由不用同样的方法——即将力处理为等于1的趋向性方法——去处理具有因果性质的所有效应（所有prima facie［第一眼所见］决定论性质的效应，例如库普顿效应）。

（6）当然，在构思此书的时候（大约是1953年）我已经找到了一些新论据。其中一些见新近出版的《探究的逻辑》德语第七版（1982年）的新附录。我希望能在《科学发现的逻辑》的下一个英文版中收录它们。