频率理论的成功之处
无论我们用何种方式来诠释科学中的概率陈述，频率诠释都无疑具有根本的重要性，因为我们交付给经验检验的总是频率陈述。基于这个原因，我将首先讨论在《逻辑》中占据了较长篇幅（第7章）的一些问题。
当我写作《逻辑》中的第7章时，冯·米泽斯那所谓随机性（或赌博系统的无用性）公理或公设正成为人们关注的焦点。
卡尔·门格尔是这样论述那个局面的[6]：“就在那时，发生了第二个被证明对瓦尔德后来的工作和生活起到了关键作用的事件。维也纳哲学家卡尔·波普尔……试图明确随机序列的概念，并用此弥补冯·米泽斯集合定义中的种种显而易见的缺陷。我（在石里克的哲学小组中[7]）听到了关于波普尔概念的半技术性阐述，之后我请那个人在数学研讨会上详细讲解其中的所有要点。瓦尔德对此非常关注[8]，随后他得出了自己的结论，其结果就是他关于集合概念的自相一致性的高水准论文……刊载于《数学研讨会报告集》……这些关于集合以及时间序列……的研究是在摩根斯坦的[9]建议下进行的，正是经过这些研究工作之后，瓦尔德将注意力转向了统计学的基本理论。”[10]
我在此提及这件事情是有原因的，这件事对瓦尔德和我来说都很重要。因为瓦尔德的工作是对我工作的一个推广，无论在范围上还是在深度上都远远超出了我在此领域中预想的界限。（因此我从未就此论题再发表过任何论文，我在《逻辑》中指出了这一点。）粗略地说，瓦尔德用了一种“对角论证”的东西，这使我们可以构造出一些对赌博系统的任何可数集都不敏感的序列。
简言之，瓦尔德的结果是这样的：他表明，给定赌博系统的任何可数集，都存在一些集合——实际上是整个集合连续统——它们对所有这些赌博系统都不敏感（换言之，存在一些具有收敛频率的序列，它们是赌博系统无法影响到的）。他进而表明，如果这个赌博系统集是“依据结构方法来定义的”，那么我们就能有效地构造出一些集合实例，它们对所有这些赌博系统都不敏感。[11]
在阿隆索·丘奇的一篇论文中，他对瓦尔德的结果[12]做了最后修正。瓦尔德是在一个较为粗略的意义上使用“依据结构方法来定义”和“可以被有效地［effectively］构造”这两个术语的：他曾简单地断言，对于任意一个（可数的）赌博系统集，无论我们依据什么指示或方法构造出属于此集的所有系统，这种指示或方法都可被用来构造出一些从此集的所有赌博系统来看对选择不敏感的集合。
而丘奇指出[13]，在这种情形中我们可以应用有效可计算性［effective calculability］的概念，他曾在1936年提出了一个针对此概念的形式定义。他重新提到了冯·米泽斯，后者严厉批判了[14]所有像科普兰一样的人——他们研究那些有可能用某种规则加以构造的集合；[15]他还更严厉地批判了像我这样的人——我们曾给出过具体的构造方法。[16]对于这种序列，必定总会存在成功的赌博系统，这是因为这些序列可以通过数学构造而产生；冯·米泽斯指出，对于这些序列，总存在更成功的赌博系统。
在我看来，这从不构成对我的理论的真正反对。我想做的是推导出概率理论的形式表述，而我依据的是下述假定：序列第n个元素的概率独立于其所有前导的特性。但丘奇认为冯·米泽斯的反对意见很重要。他的回应是，任何能应用在实践中的选择系统（赌博系统）都应当能允许我们有效地计算出被选择的元素（为了能对它们进行“赌博”）。因此他提出下述定义随机序列的方法：不改变冯·米泽斯第一条件（“收敛公理”），而改变冯·米泽斯第二条件（“随机性公理”或“排除赌博系统公理”）以满足下述要求，即随机序列应当对所有有效可计算的选择函数不敏感。
丘奇用这种方法排除了所有有效可计算的——也即所有在实践中能应用的赌博系统（它们在数学上都是精确可表达的），在我看来他也就成功地精确刻划了冯·米泽斯所考虑的那类集合的性质。丘奇表明，在这个情形中也可以应用瓦尔德的证明。[17]因此我们就证明了集合——或丘奇所谓的“随机过程”——的存在。
在我看来，这些结论非常完备地证明了冯·米泽斯的频率理论，而这证明也是必要的。这些结论不仅堵住了所有批评者的嘴巴，而且也给所有反对“收敛公理”（或“极限公理”）的人（譬如我）一个满意的答案。
因为丘奇表明，波雷尔的一个最重要的结论[18]也可以扩展到丘奇的“随机序列”——至少可以扩展到具有两个特性“0”和“1”的随机序列，只要它们为等分布，即p（0）=p（1）=½。[19]
我记得丘奇的结论是这样的：如果我们考虑所有可能的有限“交错序列”——即所有可能的有限的0和1序列——那么在丘奇的意义上几乎所有这种序列都是随机序列。
这显然暗含了以下两点：第一，几乎所有交错序列在无穷延伸的情况下都是收敛的；第二，几乎所有这种序列都具有“似偶然的”或“随机的”性质。它还进一步暗含着这样的观点：这种随机序列是存在的。
在这里“几乎所有”的意思是：将0和1序列诠释为介于零和一之间实数的二进位分式展开式，我们将发现，那些不是随机的展开式，也即不满足丘奇两个随机性条件的展开式，构成了一个零测度集。
为了直观地理解这个定理，对于具有½概率的交错序列，我们可以考虑长度为2、4、6…的所有可能序列，并以长度排序。（考虑到本文的篇幅，我下面仅给出最初的两个集。）
长度2：序列数：4
00 10
01 11
长度4：序列数：16
0000 1000
0001 1001
0010 1010
0011 1011
0100 1100
0101 1101
0110 1110
0111 1111
一般情况下，长度为n的不同序列的数量为2n。
伯努利很早以前就发现了下述规律：
（1）完全等分布序列的相对频率随其长度的增长而减少。（对于长度为2的序列，其相对频率为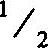
；长度为4，相对频率为
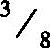；长度为6，相对频率为
。）
（2）然而，几乎等分布序列的相对频率随其长度的增长而增加。（至少要写出长度为6的序列才能较为明显地看出这一点。）
（3）对于那些在直观上具有似随机性质、具有良好逼近的、对“正规序数选择”不敏感的序列，其相对频率随其程度的增长而增加。（要相当长的序列——至少6和8——才能较为明显地看出这一点。）
如果序列不断增长，大尺度上的比例将非常接近于p（0）=p（1）=½，而随着选择方法越来越多，大尺度上的比例也将变得越来越不敏感。这样一来就得到了我们的定理。
根据这个结论，现在让我们来考虑针对收敛公理的那种常见批判，它是这样的：
（a）假设某个无法依据数学规则来计算的序列是收敛的，这种假设毫无意义；
（b）根据概率理论，所有序列都是可能的，也是和任何概率假定相容的，因此这对于下述序列[20]
010011000000111111000000000000000000111111111111111111
也同样适用，此序列的频率在½和⅓之间振荡，因此不是收敛的。但是，因为这个发散序列显然是一个可能序列，因此不容许将它排除。
现在我可以给出对这个反对观点的回应：
（a）几乎所有依据数学规则不是有效可计算的序列都具有收敛的频率。
（b）虽然确实存在发散序列，但因为它们是发散序列，我们便可以忽略它们。这就使我们得出稍微有些理想化、简化的理论。
因此，“收敛公理”或（[21]冯·米泽斯所谓的“极限公理”）就完全摆脱了它那表面上遭人非议的性质。它不再是一个武断的假设，而是假定了一个具有理想化的、简化性质的定理。它不再适用于经验上非存在的无穷序列，而是仅仅理想化了某种特性，此特性为几乎所有极长的有限序列所共有，而且当序列的长度增加时，相当多的有限序列都拥有此特性。
这一切都非常直白，也非常令人满意；我要重申的是，在我看来，它完全证明了频率方法的正确性。
但正是这个对频率方法的证明取代了频率理论本身：恰在我们能从数学上完全证明频率理论的时刻起，频率理论就成为过时的东西了。因为证明了频率理论的那个理论本身在冯·米泽斯的意义上并非频率理论：它在本质上是一个测度可能性或可能性集的理论，就像经典理论一样（最初是来自于伯努利的工作）。它可以被称作“新经典”理论。因为它能证明频率理论，因此我们就认为它是更强的理论。实际上，它使得频率理论成为冗余。换言之，一旦实现了伯努利的目标，在经典理论或不如说新经典理论和频率理论之间的鸿沟上搭起一座桥梁，那么后者也就在这个证明过程中丧失了独立的存在性，而成为前者的一部分。