关系概率和绝对概率
在讨论概率计算的诠释时我们要涉及的只是两个公式，第一个是
用语言来表述就是“给定b的前提下a的（相对）概率等于r”，其中r是介于0和1之间（包括极限）的某个分数。
第二个公式是
即“a的（绝对）概率等于r”。
给定b的前提下a的相对概率有时也被称为“在条件b下a的条件概率”；而a的绝对概率有时也被称为a的“验前”［prior］、“初始”或先验概率。
如果我们在频率诠释（在《逻辑》中有详细讨论）的意义上诠释
（R），那么
p（a，b）=r
就变成了“参考类b（或参考序列b）之中a的相对频率等于r”。
另一方面，
p（a）=r
是无法依据频率术语来诠释的（除非是以某种平凡的方式——将参考类b视为“已被了解的”）。因为如果不限定“在欧洲鸟类中”或给出类似这样的已知情况，那么说“麻雀以某种频率出现”是毫无意义的。但是我们也可以依据频率术语之外的一些术语来很容易地诠释
例如我称之为概率的“逻辑诠释”就能做到这一点。在这里我们令字母“a”和“b”等等表示陈述的名字。那么a的绝对逻辑概率——即p（a）——就是我在《逻辑》中所谓“逻辑概率”：它的值r越大，陈述a的内容就越少。换而言之，a的内容越丰富，它的绝对逻辑概率值就越小。这一点有下述事实为证：如果从断言a“明天将会下雨”无法推出断言b“下周星期六将会放晴”（如果a是重言式那么它是可以推出b的），那么a显然比断言ab“明天将会下雨和下周星期六将会放晴”更概然。
有时人们会认为绝对概率这个概念是无意义的；确实，正如我们所知，很难在频率诠释中赋予它有用的意义。但即便是在频率理论中我们也不能说p（a）就是无意义的。因为我们可以借助相对概率来定义绝对概率的意义。
为了理解这一点，我们首先得知道，所有概率理论都能施行下述两种操作：第一，a和b的合取或积或交集，在这里我们表示为“ab”（读作“a和b”）；第二，a的否定或补集，表示为ā（读作“非a”）。如果引入这两个概念，那么aā就是系统中的一个自相矛盾或空的元素（事件、类或陈述等等），而aā的否定——即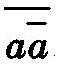
——就成为一个“完全的”或重言性质的元素，例如一个重言陈述。我们可以用“t”（即重言式）来表示
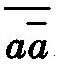。那么我们可以将绝对概率定义如下：
既然我们已经依据相对概率定义了绝对概率，那么它也必定是“有意义的”。如果我们假定一个有限论域——例如有n个元素——那么从相对频率的角度而言下式
的意义就是完全明确的：p（a）=r断言了在n个元素的论域中nr个元素具有特性a。有人认为p（a）在频率理论中是无意义的，那是因为事实上我们通常都不假定我们实际生活于其中的论域是有限的。（至少我们通常都不假定它最终是有限的。）而在某一无穷论域中，“p（a）=r”的意义确实不甚明朗，因为如果它既非1也非0，那么在数学意义上它一般都不确定。
在有限论域中我们也可以根据绝对概率来定义相对概率，方法如下
这个定义可以推广到无穷论域中去，但必须加上条件p（b）≠0。（在有限论域中如果p（b）=0那么我们可以令p（a，b）=1。）
在下文中我将主要探讨相对概率；也就是说，我将探讨
的种种诠释。如果涉及到绝对概率，那么我们就用（DA）的方式，根据相对概率来定义它。
在这里我不要求读者们了解任何实际的概率计算知识，其公理和基础推导可见《逻辑》附录*ⅳ和*ⅴ。