沿海三大经济区海洋产业与区域经济联动关系传统分析
由于海洋产业数据的限制以及数据统计方式的不同,本部分的研究数据主要选取了是2013—2017年的三大经济区相关年鉴中的海洋产业相关数据,并用传统的分析方法研究海洋产业与区域经济之间的关系。
(一)环渤海经济区海洋产业与区域经济联动关系的传统分析
基于2013—2017年环渤海经济区海洋产业规模的扩大,以及该经济区的经济发展,得到其相关指标的变化如表7-1所示。
表7-1 环渤海经济区域经济与海洋产业规模变化[51]
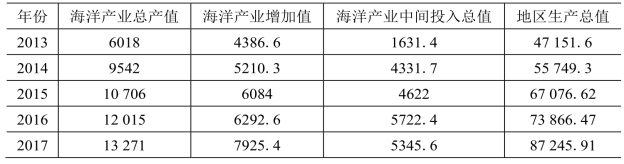
由表7-1可知,在直观的角度上发现2013—2017年各个指标的产值都在不断上升,海洋产业总产值和地区总产值基本翻了一倍,而海洋产业中间投入总值的年增长率最大,说明近几年海洋产业发展前景较好,能够吸引其他企业对海洋中间相关产业的投入。为了能够对该经济区的海洋产业与区域经济进行整体直观性的分析,根据上述相关计算公式,可得出环渤海经济区的贡献度、拉动度以及相对增长率等指标的计算结果如表7-2所示。
表7-2 环渤海经济区海洋产业与区域经济联动关系直观分析[51]
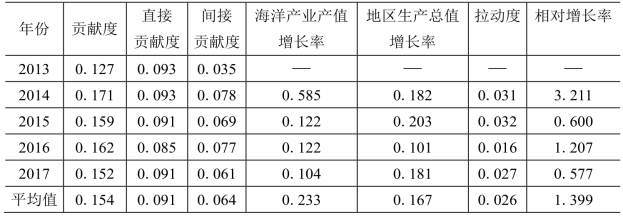
由表7-2可以看出,2013—2017年环渤海海洋产业对区域经济的贡献度变化不稳定,而直接贡献度的变化幅度较小,基本处于稳定的状态,对2013—2017年的数据取平均值,可以得出平均贡献度为15.4%,而直接贡献度和间接贡献度的均值分别为9.07%和6.4%。除此之外,还可以看出海洋产业对区域经济的拉动度的平均值为2.6%。从平均相对速率来看,其比值为139.9%大于1,说明该地区的海洋产业产值增长速率明显大于区域经济产值增速。
(二)长三角经济区海洋产业与区域经济联动关系的传统分析
随着2013—2017年长三角经济区海洋产业规模的扩大,以及该经济区经济发展水平不断提升,得到其相关指标的变化如表7-3所示。
表7-3 长三角经济区海洋产业与区域经济联动关系直观分析[51]
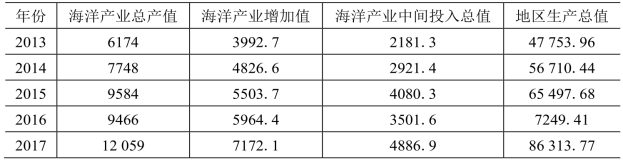
由表7-3可知,在直观的角度上发现2013—2017年长三角地区各个指标的产值都在不断上升,基本都翻了一倍。为了能够对该经济区的海洋产业与区域经济进行整体直观性的分析,根据上述相关计算公式,可得出长三角相关指标的计算结果见表7-4。
表7-4 长三角经济区海洋产业与区域经济联动关系直观分析[51]
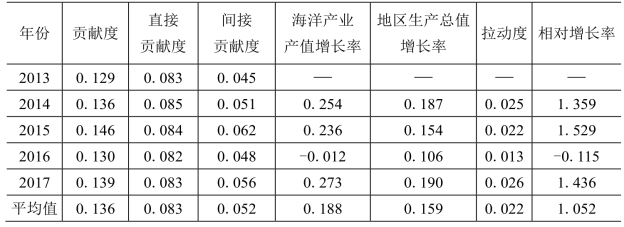
由表7-4可知,2013—2017年,长三角地区的海洋产业对区域经济的贡献度一直在13%的水平上下小幅度波动,且平均贡献度为13.7%。而间接贡献度一直比直接贡献度小,说明海洋产业相关的中间投入产值一直比海洋产业的增加值少。除此之外,还可以看出海洋产业对区域经济的拉动度较小,其平均拉动度仅为2.22%。但是从相对速率来看,除了2016年,该经济区的相对增长率均大于1,且平均相对速率比值为105.26%,说明该地区的海洋产业产值增速明显比地区经济产值增速快。。
(三)珠三角经济区海洋产业与区域经济联动关系的传统分析
2013—2017年,珠三角经济区海洋产业规模不断扩大,以及该经济区经济发展水平不断提升,从而得到其相关指标的变化如表7-5所示。
表7-5 珠三角经济区海洋产业与区域经济联动关系直观分析[51]
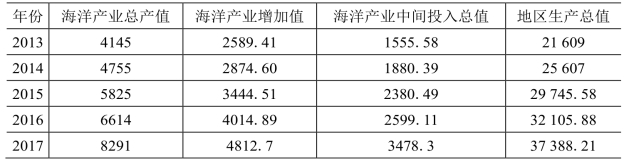
由表7-5可知,在直观的角度上可以发现2013—2017年珠三角地区各个指标的产值都在不断上升,与长三角经济区的变化趋势基本一致,即各个指标基本都实现了翻一倍。为了能够对该经济区的海洋产业与区域经济进行整体直观性的分析,根据上述相关计算公式,可得出珠三角相关指标的计算结果如表7-6所示。
表7-6 珠三角经济区海洋产业与区域经济联动关系直观分析[51]
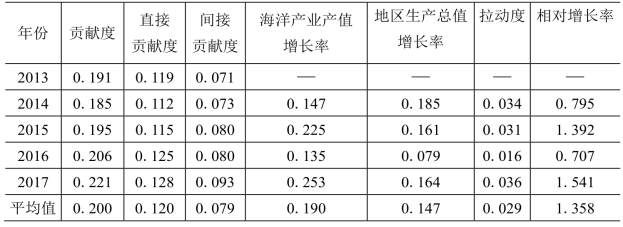
由表7-6可知,2013—2017年,珠三角地区的海洋产业产值对区域经济产值的贡献度不断增长,其平均贡献度为20.02%。针对近几年的上述指标变化,除2016年,该地区的海洋产业对区域经济的拉动度在其他年份均达到3%以上。从相对增长率的分析结果来看,该经济区的相对增长率变化幅度较大,最低值和最高值之间相差了一倍,但其平均相对速率仍然大于1,说明该地区的海洋产业产值增长率仍然比区域经济增长速率大。
(四)沿海三大经济区海洋产业与区域经济联动关系计量分析
为了对海洋产业产值与区域经济发展之间的联系进行计量分析,本文选取了2001—2017年各个经济区的产值原始数据如表7-7所示。
表7-7 三大经济区海洋产业与区域经济联动关系计量分析[51]
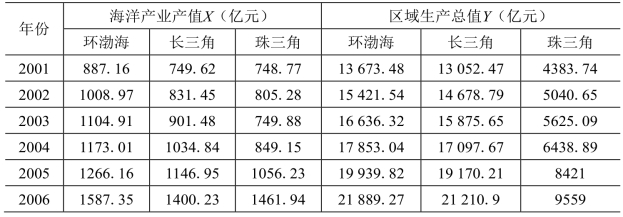
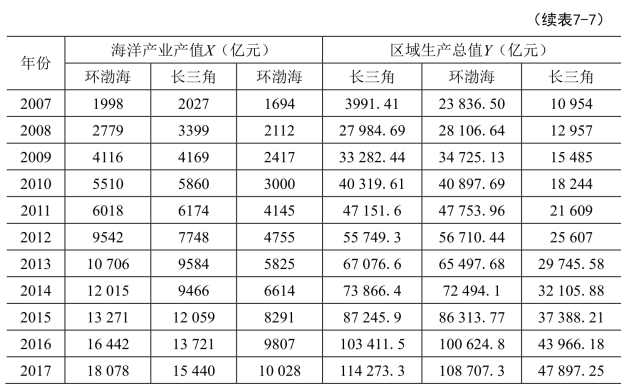
为了方便分析两个指标之间的联动作用,分别以Lnx、Lny表示各区域的海洋产业产值和经济生产总值,具体实证研究结果如下。
1.环渤海地区海洋产业与区域经济联动关系的计量分析
结合环渤海地区2001—2017年海洋产业产值与区域生产总值,利用Eviews软件对变量进行如下分析。
(1)对变量进行平稳性检验的结果如表7-8所示。
表7-8 环渤海地区变量平稳性检验[51]
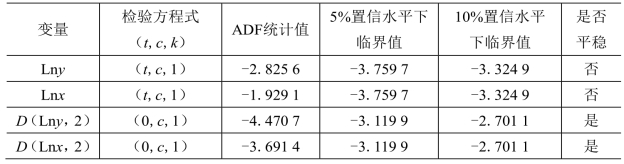
由表7-8可知,在不同置信水平下,Lny和Lnx的ADF统计值都大于临界值,说明这两个序列都不平稳。为了保证序列的平稳性,分别对其进行二阶差分,结果表明二阶差分序列都平稳。因此,可以对两个变量进行协整检验以验证它们之间的关系。
(2)协整检验和因果检验
采用Johansen检验方法通过Eviews软件对Lny与Lnx进行协整检验,分析结果见表7-9。
表7-9 环渤海地区变量协整关系检验[51]

由表7-9可知,Lnx和Lny这两个变量的统计值为28.345 34,且大于5%置信水平下的临界值,说明拒绝原假设,即可以认为上述两变量之间具有协整关系,也就是说这两个变量之间存在长期的相关关系。为了验证Lnx和Lny之间是否存在明显的因果关系,下面通过Eviews软件对其进行Granger因果检验,得到的结果见表7-10。
表7-10 环渤海地区变量格兰杰因果检验[51]
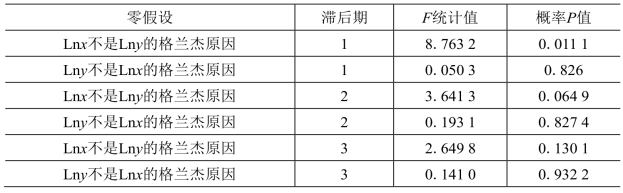
表7-10结果表明,在滞后1期时,得到的概率P值为0.011 1,小于5%的置信水平,说明拒绝原假设,即环渤海地区的海洋产业产值对区域经济产值仅存在单向的Granger因果关系;在滞后2、3期时,得到的概率P值为均大于5%的置信水平,说明接受原假设,即环渤海地区的海洋产业与区域经济产值之间不存在Granger因果关系。
(3)回归分析与结果
基于对数据进行了协整检验和Granger因果检验,接下来利用Eviews软件对变量Lnx和Lny进行回归分析的结果见表7-11。
表7-11 环渤海地区变量直接回归结果[51]

由表7-11可知,在5%的显著性水平下,DW统计值为0.587 833。而当n=17,k=1时,查表得知DW临界值分别为:DL=1.13、DU=1.38, 由于DW统计值<临界值DL,说明存在自相关。且对变量进行White检验的结果显示不存在异方差。因而只需要消除自相关即可,即采用广义差分法通过Eviews软件对回归分析进行调整,得到调整后的结果见表7-12。
表7-12 环渤海地区变量广义差分回归结果[51]

由表7-12可知,调整后的回归结果中DW值为1.6949,且DU<DW<4-DU,说明调整后的数据序列已经不存在自相关。且常数项和解释变量Lnx的T统计值均大于临界值,同时概率P值也小于0.05,说明在5%的置信水平下,回归结果是显著的。此外,可决系数超过0.9,说明该回归方程的拟合优度较好。因此,可以说明调整后的回归结果具有较强的可靠性,可以适用于实证结果分析。其中Lnx的系数为0.617 704,表明在环渤海地区的海洋产业产值Lnx每增长1个百分点单位,区域经济Lny也就增长0.617 704个百分点单位。
2.长三角地区海洋产业与区域经济联动关系的计量分析
结合长三角地区2001—2017年海洋产业产值与区域生产总值,基于Eviews软件采用计量分析法得到相关实证研究结果,具体的分析过程如下:首先,对变量进行单位根检验,结果发现在5%和10%不同的置信水平下,两个序列Lny和Lnx的ADF统计值都大于临界值,说明这两个序列都是不平稳的;其次,分别对其进行二阶差分后再进行单位根检验,结果表明调整后的序列是平稳的,即Lny和Lnx符合同阶单整;然后,对Lnx和Lny进行协整检验,结果表明其极大似然比为32.823 73,且大于5%置信水平下的临界值20.261 84,说明拒绝原假设,即有95%的可能性证明两者之间存在协整关系,即变量间存在一定的长期关系,从而能够对变量进行回归分析;最后,对变量进行Granger检验,结果显示在滞后1、2、3期时,海洋产业产值对区域经济产值存在明显的影响关系,而这种影响关系仅仅是单向的,即反过来不成立。由于两者之间存在长期均衡的关系,现在直接对Lnx和Lny进行回归,发现两个变量之间存在自相关,为了消除自相关,基于广义差分法得到的回归结果见表7-13。
表7-13 环渤海地区变量广义差分回归结果[51]

由表7-13可知,调整后的回归结果中DW值为1.3299,且DU<DW<4-DU,说明调整后的数据序列已经不存在自相关。且常数项和解释变量Lnx的T统计值均大于临界值,同时概率P值也小于0.05,说明在5%的置信水平下,回归结果是显著的。此外,可决系数超过0.8,说明该回归方程的拟合优度良好。因此,可以说明调整后的回归结果具有很好的可信度,可以适用于实证结果分析。其中Lnx的系数为0.583 177,说明长三角地区的海洋产业产值每增长1单位,区域经济就增长0.583 177单位。
3.珠三角地区海洋产业与区域经济联动关系的计量分析
结合珠三角地区2001—2017年海洋产业产值与区域生产总值,基于Eviews软件利用计量分析法得到相关的实证研究结果,具体的分析过程如下:首先,对变量进行平稳性检验,发现在5%和10%的置信水平下, Lny和Lnx序列的ADF统计值都大于临界值,说明这两个序列都是不平稳的;其次,分别对其进行一阶差分后再进行单位根检验,结果表明调整后的序列是平稳的,即Lny和Lnx符合同阶单整;然后,对Lnx和Lny进行协整检验,结果表明其统计值为34.855 56,且大于5%置信水平下的临界值20.261 84,说明拒绝原假设,可以说明两变量间具有长期的相关关系;最后,Granger检验结果显示,在滞后1、2、3期时,发现珠三角地区的海洋产业对区域经济促进作用不明显,而区域经济发展对海洋产业促进作用却十分明显,这与其他两个经济区的实证研究结果不同,具体结果见表7-14。
表7-14 珠三角地区变量格兰杰因果检验[51]
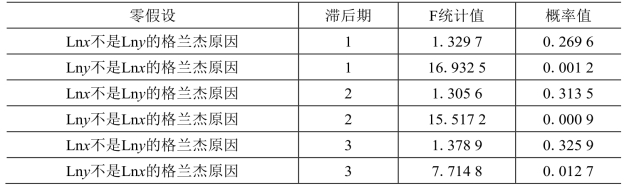
由表7-14可知,珠三角地区的Lnx和Lny存在协整关系,海洋产业产值和区域经济产值之间存在长期均衡的关系,直接对以上两个变量Lnx和Lny进行回归,结果表明在5%的显著性水平下,基于White检验方法,得到的卡方统计值大于临界值,说明存在异方差。为了消除异方差,采用加权最小二乘法对回归结果进行修正,得到的回归结果见表7-15。
表7-15 珠三角地区变量加权最小二乘回归结果[51]

由表7-15可知,在5%的显著性水平下,其概率值小于0.05,说明异方差现象己消除。但是DW统计值为0.743 887不在(DU,4-DU)范围内,所以存在自相关。因此,需要采用广义差分法来消除自相关,得到调整后的结果如表7-16所示。
表7-16 珠三角地区变量加权与广义差分回归结果[51]

由表7-16可知,在5%的显著性水平下,其DW统计值为1.4034,且DU<DW<4-DU,说明调整后的数据序列已经不存在自相关。此外,可决系数超过0.9且接近1,说明该回归方程的拟合优度良好。因此,可以说明调整后的回归结果具有很好的可信度,可以适用于实证结果分析。其中Lny的系数为0.791 425,表明在珠三角地区内,区域经济产值Lny每增长1个单位,海洋产业产值Lnx就增长0.791 425个单位。
