三、研究方法
1.主成分分析法
主成分分析法又称主分量分析法，其宗旨是通过降维处理简化数据集，是一种线性变换的统计方法。主要是通过正交变换，将一组可能具有相关性的变量转换为一组具有线性不相关的变量，转换后得到的变量即主成分。这种方法主要适用于多变量问题。对于变量太多的实际问题，在进行定量分析时分析过程过于复杂。因此，人们希望在分析一些具体的问题时，能够通过更少的指标变量获得更多的信息。主成分分析法的降维处理能够在保持变量总方差不变的情况下得到少数的主成分变量，主成分变量之间互不相干，且最大程度地保留了原始变量的信息，最终使分析指标简单化、直观化。应用主成分分析对运河沿线城市的旅游竞争力进行分析，其具体操作步骤如下。
现假设存在m个城市，选择确定p个评价指标对各城市的旅游竞争力进行衡量，构建评价样本矩阵。
（1）借助计量分析软件对原始指标数据进行标准化处理；
（2）对标准化处理后的样本数据，计算各指标的相关矩阵R；
（3）构建雅各比矩阵计算相关矩阵R的特征值λ；
（4）选用判定准则对主成分变量分数进行确定，在此以“特征根植大于或等于1，或者方差累计贡献率大于75%”作为判定准则；
（5）根据主成分载荷矩阵，对那个主成分变量的含义进行分析说明；
（6）根据主成分变量的得分值，利用计量分析软件的“Transform”功能下的“Computer Variable”功能，对各因子对应的主成分得分进行计算并排序；
（7）计算最后的旅游竞争力综合得分值，具体公式如8.1、8.2所示。
其中
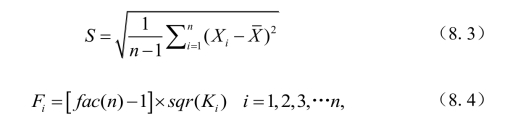
式中，Xi表示各项指标的初始值；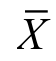
为各项指标初始值的平均值；Yi表示对各项指标进行标准化处理以后得到的指标数值；S表示各项指标的初始值的标准差值；n为观察样本的个数。式中Fi表示的是主成分变量的得分值，fac(n)-1表示的是n个未旋转因子的得分值，sqr(Ki)表示主成分特征根的平方根。
2.聚类分析法
聚类分析法也是一种理想的多变量统计方法，也称为群分析或点群分析方法。聚类分析法又包括分层聚类法和迭代聚类法。聚类分析方法的基本思想是通过建立分类，在没有先验知识的情况下，将一些样本或者变量数据根据其各自的特征，按照在性质上的亲疏程度进行自动分类。被研究的样本或者指标变量之间存在程度不同的相似性，这种相似性就是所谓的亲疏关系，通常以样本间距离来衡量。根据大量样本中的多个观测指标，可以发现一些能够度量样本或指标之间相似程度的统计量，将找到的这些统计量作为依据对样本或变量及逆行分类，将一些相似度较高的样本或指标聚合为一类，其他样本或指标聚合为另一类，一直到将所有的样本或指标聚合完毕。
在聚类分析中，最为重要的就是聚类要素的选择，被聚类的对象是由多个要素组成的，通过聚类分析得到的结果准确和可靠。由于所搜集到的要素数据通常是具有不同的量纲和数量级，在进行实证分析时由于数值不同的量纲会导致结果受到影响。因此，在进行实证分析之前，要对搜集到的要素数据进行标准化处理。假设有m个聚类的对象，每一个聚类对象都由n个要素构成，它们所对应的要素数据如表8-2所示。
表8-2 聚类要素与要素数据
（续表8-2）
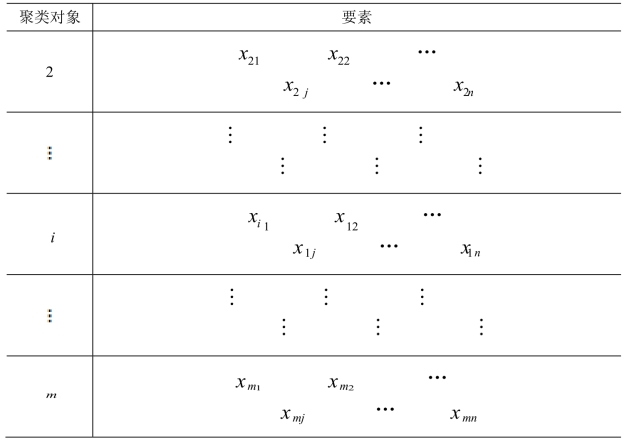
在聚类分析中，比较常用的聚类要素的数据处理方法主要包括如下几种。
（1）总和标准化法
总和标准化指的是分别对各聚类要素所对应的数据的求和，以各要素的数据除以该要素的数据总和，即
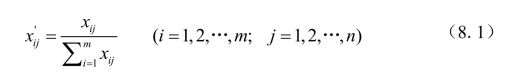
利用总和标准化计算得到的新数据，需要满足
（2）标准差标准法
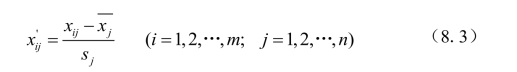
标准差标准法所得到的新数据，各要素的平均值为0，标准差为1，即有
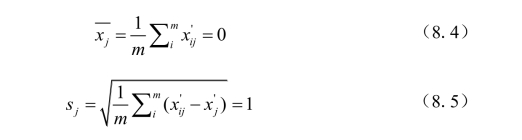
（3）极大值标准化
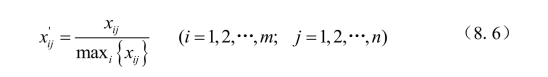
经过极大值标准化，处理后所得到的新数据，各要素的极大值为1，其余各数值小于1。
（4）极差的标准化
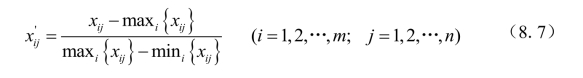
经过极差的标准化，数据处理后得到的新数据，各要素的极大值为1，极小值为0，其余的数值均介于0和1之间。