幂式范数的多指标间补偿原理

滥熵自妥协规划（compromise programming，cp）理论妥协解概念的多指标妥协评价方法，特别适用于指标难于公度的和存在冲突情况下的综合评价理论。它的多指标聚合机制通过Minkowski’s Lp-metric 与理想解得以实现[132]：

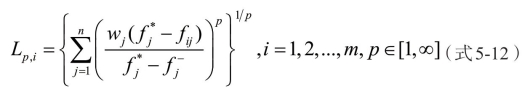
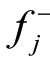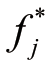其中 fij（ i=1，2，...，m ，j=1，2，...，n ）表征评价指标Cj下评价方案Ai 的具体评价分数，评价指标 Cj的重要度用wj（j=1，2，...，n ）来表征，全部评价方案关于评价准则 Cj的正负参照解分别用 和 表示。

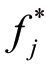据式（5-12）， Lp-metric 显然呈现如下物理特性：首先，偏离函数被该范数用正理想解和负理想解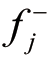间的相对偏离替代，这样做是为了将所有评价值规范于相同值域，进而不同量纲评价指标间的公平比较便得以实现。其次，关联参数 p 的改变将显著影响该范数。当 p 值不断增大时，Lp-metric值却在不断下降（即有L1，i≥ L2，i≥ …≥ L∞，i）。与此同时，距离理想值最远的对象的偏离得到了最大的指标权重。此外，有两种极端情形需要注意，一是当 p=1 时，这意味着对所有对象与理想解的偏离是“等量齐观”的，即决策者认为这些偏离具有同等重要程度；二是当 p= ∞ 时，此时以最大偏离是着所有对象整体偏离的执牛耳者。

当我们从决策分析理论的角度进行分析时，采用 Lp-metric聚结机制体时，作为最接近理想参考值的应该是所获得的最优评价方案。此外，在评价指标Cj下，与对应的理想参考值相比较，评价方案Ai的未达到或遗憾（regret）程度可以用进行解释。顺着这个思路，如果 p 值较小 （诸如 p=1）时，个体指标遗憾的平均和的最小化可以用来表示〔相对而言，它也同时强调指标整体效用（utility）的要实现最大化〕；随着p 值的不断增大，取值较大的个体指标偏离逐渐获得了更大的指标权重，特别是当 p=∞ 时，变成了最大的个体指标遗憾最小化，此时最差指标控制着评价方案的整体性能，该逻辑贴合经济管理学中的“木桶原理”。依据此逻辑推论，显然评价专家对最大偏离（遗憾）的关注程度可以基于参数 p 在值域[1，∞]中选取不同的数值来刻画。进而一种在各准则与之相应的理想解的偏离的加权和最小化中妥协的达成方式能够基于参数 p 在值域[1，∞]中选取不同数值来表达。特别地，当 p=1 时， 几乎忽略了个体遗憾而凸显群体效用；相反，当 p=∞ 时，则几乎完全凸显个体遗憾而忽视了群体效用。在此两极端情况之间，不同的补偿度就通过参数p 在值域[1，∞]中选取不同数值而获得。基于此，凭借 Lp距离思想的拓展得到指标聚合的新机制，换句话说，参数 p （1 ＜ p ＜ ∞）承担着“平衡”整体指标效用和最大个体指标遗憾的功能。